Подобие гидравлических турбин

Для обобщения и анализа исследований индивидуальных характеристик (рисунок 8.23) модельных образцов турбин турбобуров заданных размеров (D_M , _M и т.д.), испытанных в определенных условиях, т.е. при определенном расходе жидкости Q_M и ее физических свойствах, при создании новых турбин пользуются общей теорией подобия, которая предполагает:

1) геометрическое подобие - пропорциональность линейных размеров, шероховатостей модели и натуры и равенство сходственных углов входных и выходных элементов лопаток;

2) кинематическое подобие, т.е. подобие полей скоростей (полигонов) в сходственных точках модели и натуры;

3) динамическое подобие, т.е. пропорциональность сил, действующих на сходственные элементы модели и натуры.

Первое условие обеспечивается одинаковым масштабом линейного моделирования и равенством конструктивных углов:

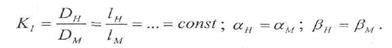
Кинематическое подобие предусматривает соотношения скоростей:

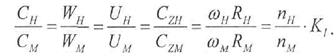
Поскольку основными силами, действующими в потоке жидкости, являются силы вязкости и инерции, условие динамического подобия соответствует равенству чисел Рейнольдса: R_{e Н} = R_{e M}.

В большинстве случаев турбины работают в условиях автомодельности, когда определяющим фактором является не число R_e, а шероховатость, т.е. для подобия достаточно двух первых условиях.

Чтобы определить показатели работы турбин данной серии (К_е = const) при различных расходах и физических свойствах жидкости, необходимо составить следующие соотношения.

Так, числа оборотов вращения вала двух турбин одной серии равны:

Зная, что осевая скорость С_z турбины равна C_z = , получим

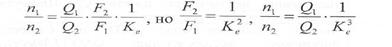
вращающие моменты:

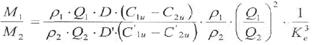
мощности турбины:

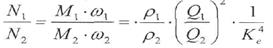
перепад давления в турбинах:

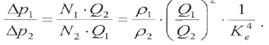
Если турбины турбобура работают на одной и той же жидкости (р = const), топри изменении подачи насоса на основании общих формул подобия можно определить все показатели работы:

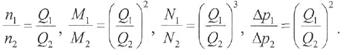
При испытаниях турбин моделирование не применяется, но, при пересчете характеристик односерийных турбобуров различных диаметров формулы подобия необходимы.