Ошибки по регулярному задающему воздействию х(t)

Для изучения свойств точности системы ошибки в установившемся режиме работы системы вычисляются для трех пробных регулярных входных воздействий:

а) 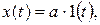a = const – постоянная составляющая,

б) 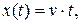v = const – скорость входного воздействия,

в) 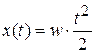, w = const – ускорение входного воздействия.

Для расчета характеристик точности системы часто используют метод коэффициентов ошибок, применимый, когда:

- задающее воздействие является медленно меняющейся функцией времени по сравнению со временем переходного процесса системы;

- ошибки рассчитываются в установившемся режиме работы системы, то есть для моментов времени, намного превышающих время переходного процесса, t >> t_n .

Эти допущения позволяют ограничиться тремя слагаемыми при разложении передаточной функции W_{e x} (s) по степеням s относительно s = 0.

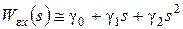, (2.89)

где g₀, g₁, g₂ - коэффициенты ошибок по постоянной составляющей задающего воздействия x(t), по его скорости и ускорению.

Итак, с учетом разложения (2.89) выражения (2.83) при F(s) = 0 имеем:

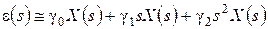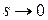, , (2.90)

и, применяя обратное преобразование Лапласа к обеим частям уравнения (2.90), получим

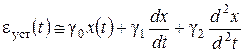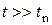, . (2.91)

Для вычисления коэффициентов ошибок g₀, g₁, g₂ либо делят "уголком" полином числителя на полином знаменателя передаточной функции 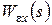(это удобно делать в цифрах), либо их получают в результате приравнивания коэффициентов при одинаковых степенях s левой и правой частей соотношения, получаемого из (4.5) с учетом разложения (4.7)

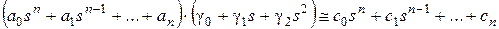. (2.92)

Для повышения точности системы следует:

· повышать ее порядок астатизма (порядок астатизма системы определяется числом интегрирующих звеньев передаточной функции W(s)). Статические ошибки астатических систем всегда равны нулю, так как g₀ = 0 (статической называется ошибка по постоянной составляющей входного воздействия, то есть при х(t) º a). Для астатической системы второго порядка ошибка и по скорости входного воздействия равна нулю, так как для этой системы и g₁ = 0.

· повышать коэффициент усиления k системы в разомкнутом состояна - задержки на период квантования; б - умножения на постоянный коэффициент; в — сложенияии.

2.8.2. Ошибки, вызванные помехой f(t)

Случайная составляющая e_сл(t) ошибки системы в данном случае вызывается действием помехи f(t). Рассматриваемая система является линейной и стационарной. Помеха f(t). – стационарный случайный процесс с нулевым математическим ожиданием и спектральной плотностью S_f(w). В этих условиях случайная составляющая ошибки e_сл(t) также представляет собой стационарный случайный процесс с нулевым математическим ожиданием и спектральной плотностью

S_e(w) = S_f(w)×½K_ef(jw)½², K_ef(jw) = W_ef(s)ç_s=jw . (2.93)

Ее дисперсия определяется выражением

s_e² = 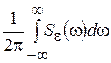(2.94)

или, учитывая, что в рассматриваемом задании помеха представляется как белый шум и имеет постоянную спектральную плотность мощности S_f(w) » S_f(0) = const,

s_e² = 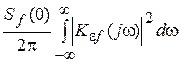. (2.95)

Формулы для вычисления интегралов вида:

J_n = 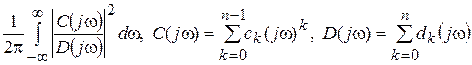(2.96)

приведены в [ 3 ] на стр. 321 – 322 (n – порядок системы).

Следует обратить внимание на совмещение обозначений: C(s) – знаменатель передаточной функции W(s) (см. (4.4)), а С(jw) - числитель комплексного коэффициента передачи K_ef(jw) в формуле (4.13). Кроме этого, в этих формулах изменен порядок индексации коэффициентов c_i: i = 0, 1, 2,…,n – 1 и d_j: j = 0, 1, 2, …,n , т.е.

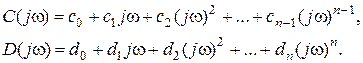(2.97)

Для исходной системы третьего порядка, т.е. при n = 3, интеграл J₃ имеет вид

J₃ = 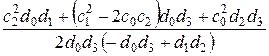. (2.98)

Для результирующей системы четвертого порядка, т.е. при n = 4, формула для интеграла J₄ имеет вид

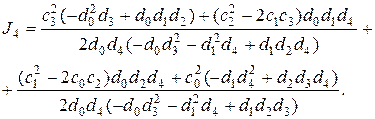(2.99)

Удобно дисперсию ошибки представлять в виде

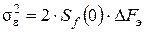, (2.100)

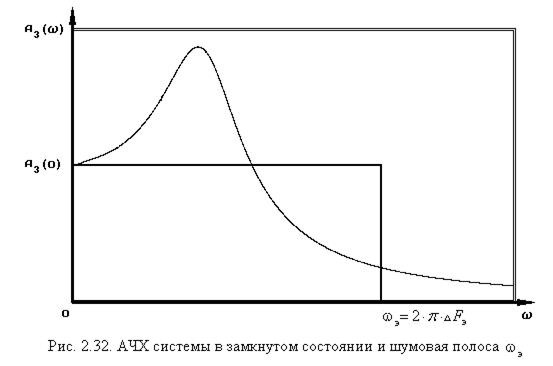
где DF_э = 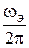- эквивалентная шумовая полоса рассматриваемой системы, равная полосе пропускания некоторой эквивалентной системы, имеющей прямоугольную амплитудно-частотную характеристику (АЧХ) замкнутой системы с тем же коэффициентом передачи на нулевой частоте, что и в рассматриваемой системе (см. рис. 10).

Таким образом,

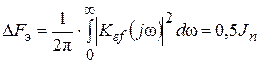. (2.101)

Именно значение DF_э характеризует помехоустойчивость системы. Чем шире полоса DF_э, тем меньше помехоустойчивость системы.