Методические указания по выполнению лабораторной работы № 9
Целью эффективного кодирования является устранение избыточности сообщений, поскольку избыточные сообщения требуют большего времени для передачи и большего объема памяти для хранения.
Очевидно, что для уменьшения избыточности кодовых комбинаций, кодирующих символы сообщений, необходимо выбирать максимально короткие кодовые комбинации. Однако для полного устранения избыточности этого недостаточно. При кодировании необходимо учитывать вероятности появления каждого символа в сообщениях и наиболее вероятным символам сопоставлять короткие кодовые комбинации, а наименее вероятным - более длинные.
В качестве иллюстрации - простой пример. Пусть сообщение может состоять из двух слов. Длина первого - один кодовый символ, второго - три кодовых символа. Вероятности появления слов в сообщении соответственно 0,1 и 0,9. Тогда статистически средняя длина слова в сообщении 1*0,1 + 3*0,9 = 2,8 символа. Если слова будут иметь другие вероятности, например, 0,9 и 0,1, то средняя длина слова составит 1*0,9 + 3*0,1 = 1,2 символа. Отсюда видно, что длина кодовой комбинации должна выбираться в зависимости от вероятности появления кодируемого этой комбинацией символа сообщения. Чем чаще он появляется, т.е. чем больше его вероятность, тем более короткую кодовую комбинацию ему следует сопоставить.
Формализуем задачу эффективного кодирования. Пусть входным алфавитом кодирующего отображения является множество сообщений  . Пусть выходным алфавитом кодирующего отображения будет множество В , число элементов которого равно m .Кодирующее отображение сопоставляет каждому сообщению аi кодовую комбинацию, составленную из ni символов алфавита В . Требуется оценить минимальную среднюю длину кодовой комбинации. Сравнивая ее со средней длиной кодовой комбинации, вычисленной для какого-либо конкретного кода, можно оценить, насколько данный конкретный код находится близко к эффективному, т.е. безизбыточному коду.
. Пусть выходным алфавитом кодирующего отображения будет множество В , число элементов которого равно m .Кодирующее отображение сопоставляет каждому сообщению аi кодовую комбинацию, составленную из ni символов алфавита В . Требуется оценить минимальную среднюю длину кодовой комбинации. Сравнивая ее со средней длиной кодовой комбинации, вычисленной для какого-либо конкретного кода, можно оценить, насколько данный конкретный код находится близко к эффективному, т.е. безизбыточному коду.
Энтропия сообщения А по определению
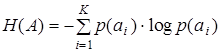 . (9.1)
. (9.1)
Средняя длина кодовой комбинации
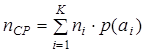 , (9.2)
, (9.2)
где ni - длина кодовой комбинации, сопоставленной сообщению аi. Максимальная энтропия, которую может иметь сообщение из nСР символов алфавита В, число элементов которого равно m, равна
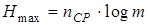 . (9.3)
. (9.3)
Очевидно, что для обеспечения передачи информации, содержащейся в сообщении А, с помощью кодовых комбинаций алфавита В должно выполняться неравенство
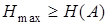 (9.4)
(9.4)
или с учетом (9.3) 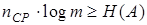 или с учетом (9.1)
или с учетом (9.1)
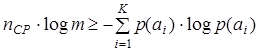 . (9.5)
. (9.5)
При строгом неравенстве (9.4) закодированное сообщение обладает избыточностью, т.е. для кодирования используется больше символов, чем это минимально необходимо. Для числовой оценки избыточности в предыдущей главе использовался коэффициент избыточности
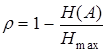 . (9.6)
. (9.6)
Поскольку из (9.3) и (9.4) следует, что 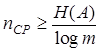 , то ясно, что
, то ясно, что
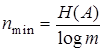 . (9.7)
. (9.7)
Тогда формулу (9.6) для коэффициента избыточности для кода можно переписать в следующем виде
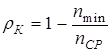 . (9.8)
. (9.8)
Под эффективным кодом понимается код, rК которого равен 0, т.е. для абсолютно эффективных кодов 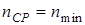 . Тогда и неравенство (9.5) переходит в равенство
. Тогда и неравенство (9.5) переходит в равенство 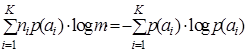 , откуда
, откуда 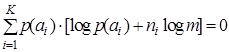 .
.
Предположив очевидное, что А не содержит элементов с p(ai) = 0, получим
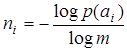 (9.9)
(9.9)
для всех i. Но отношение (9.9) не всегда дает целочисленный результат. Следовательно, не для любого набора А с заданным распределением вероятностей p(ai) можно построить абсолютно эффективный код с rК = 0. Тем не менее, всегда можно обеспечить выполнение неравенства  , умножая которое на p(ai) и суммируя по i , получим
, умножая которое на p(ai) и суммируя по i , получим
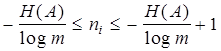 . (9.10)
. (9.10)
Неравенство (9.10) может служить критерием для оценки эффективности какого-либо конкретного кода.
Для построения эффективных кодов используются различные алгоритмы. Одним из них является код Шеннона - Фано. Код Шеннона - Фано строится следующим образом. Символы алфавита источника выписываются в порядке убывания их вероятностей. Затем вся совокупность разделяется на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковыми. Далее всем символам одной группы в качестве первого кодового символа приписывается 1, а другой группы - 0. Далее каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и т.д. Процесс повторяется до тех пор, пока в каждой группе останется по одному символу.
Пример 9.1. Закодировать двоичным кодом Шеннона - Фано ансамбль {ai} (i=1,2,...,8), если вероятности pi символов ai имеют следующие значения
| ai | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| pi | 0,25 | 0,25 | 0,125 | 0,125 | 0,0625 | 0,0625 | 0,0625 | 0,0625 |
Найти среднее число символов в кодовой комбинации и коэффициент избыточности кода.
Решение.
| ai | pi | кодовая комбинация | ni | pini | H(ai) |
| a1 | 0,25 | 11 | 2 | 0,5 | 0,5 |
| a2 | 0,25 | 10 | 2 | 0,5 | 0,5 |
| a3 | 0,125 | 011 | 3 | 0,375 | 0,375 |
| a4 | 0,125 | 010 | 3 | 0,375 | 0,375 |
| a5 | 0,0625 | 0011 | 4 | 0,25 | 0,25 |
| a6 | 0,0625 | 0010 | 4 | 0,25 | 0,25 |
| a7 | 0,0625 | 0001 | 4 | 0,25 | 0,25 |
| a8 | 0,0625 | 0000 | 4 | 0,25 | 0,25 |
По формуле (9.2) 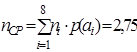 , по формуле (9.1)
, по формуле (9.1) 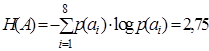 , тогда по формуле (9.7)
, тогда по формуле (9.7) 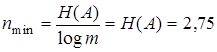 и по формуле (9.8)
и по формуле (9.8) 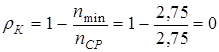 , таким образом, построен абсолютно эффективный код.
, таким образом, построен абсолютно эффективный код.
Алгоритм кодирования Шеннона - Фано имеет простую графическую иллюстрацию в виде графа, называемого кодовым деревом. Граф для кода Шеннона - Фано строится следующим образом. Из нижней или корневой вершины графа исходят два ребра, одно из которых помечается символом 0, а другое – 1. Эти два ребра соответствуют разбиению множества символов алфавита источника на две примерно равновероятные группы, одной из которых сопоставляется кодовый символ 0, а другой – 1. Ребра, исходящие из вершин следующего уровня, соответствуют разбиению получившихся групп на равновероятные подгруппы и т.д. Построение графа заканчивается, когда множество символов алфавита источника будет разбито на одноэлементные подмножества. Каждая концевая вершина графа, т.е. вершина, из которой уже не исходят ребра, соответствует некоторой кодовой комбинации. Чтобы сформировать эту комбинацию, надо пройти путь от корневой вершины до соответствующей концевой, выписывая в порядке следования по этому пути кодовые символы с ребер пути.
Рассмотренная методика Шеннона - Фано не всегда приводит к однозначному построению кода, поскольку в зависимости от вероятностей отдельных символов можно несколькими способами осуществить разбиение на группы.
Пример 9.2. Закодировать двоичным кодом Шеннона - Фано ансамбль {ai} (i=1,2,...,8), если вероятности символов ai имеют следующие значения
| ai | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| pi | 0,22 | 0,20 | 0,16 | 0,16 | 0,10 | 0,10 | 0,04 | 0,02 |
Найти коэффициент избыточности кода.
Дата добавления: 2015-07-30; просмотров: 939;
