Методические указания по выполнению лабораторной работы № 7

На основании любого из описаний группового систематического кода (системы проверочных уравнений, образующей матрицы, проверочной матрицы) могут быть синтезированы функциональные схемы кодера и декодера такого кода.

Кодер для кода, описываемого образующей матрицей G_7,4,

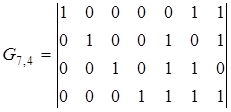
должен содержать: параллельный регистр, предназначенный для приема от источника и временного хранения четырех информационных разрядов; совокупность из трех трехвходовых сумматоров по модулю два, предназначенных для формирования значений трех контрольных разрядов; параллельный семиразрядный регистр для промежуточного хранения сформированной кодовой комбинации, которая далее может быть последовательно передана в линию связи. Соединение входов сумматоров по модулю два с выходами первого регистра выполняются в соответствии с любым из описаний кода .

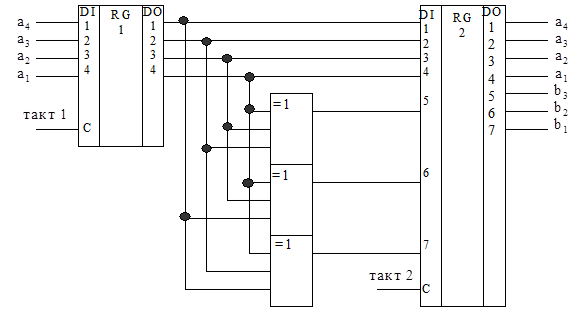
Синтезированная на основе этих рассуждений функциональная схема кодера приведена на рис.7.1.

Сложность схемы декодера для такого кода будет зависеть от того, используется ли данный код в режиме обнаружения ошибки или в режиме исправления ошибки.

Для режима исправления ошибки в составе декодера должны присутствовать следующие функциональные узлы: регистр для временного хранения принятой кодовой комбинации; устройство вычисления синдрома; дешифратор синдрома; устройство исправления ошибки; регистр для хранения исправленной информационной части комбинации.

Рис. 7.1. Кодер систематического кода (7,4)

Устройство вычисления синдрома представляет собой совокупность из трех сумматоров по модулю два, каждый из которых имеет по четыре входа, которые соединяются с выходами первого регистра в соответствии с системой проверочных уравнений, а выходы подключены к входам дешифратора синдрома. Дешифратор синдрома осуществляет формирование исправляющего вектора E_j, сумма по модулю два которого с принятой кодовой комбинацией образует переданную комбинацию. Устройство исправления ошибок может быть реализовано в виде совокупности из четырех сумматоров по модулю два, каждый из которых имеет по два входа. Первые входы сумматоров соединяются с выходами информационных разрядов первого регистра, а вторые входы подключаются к соответствующим выходам дешифратора синдрома, а выходы соединены с соответствующими входами второго регистра.

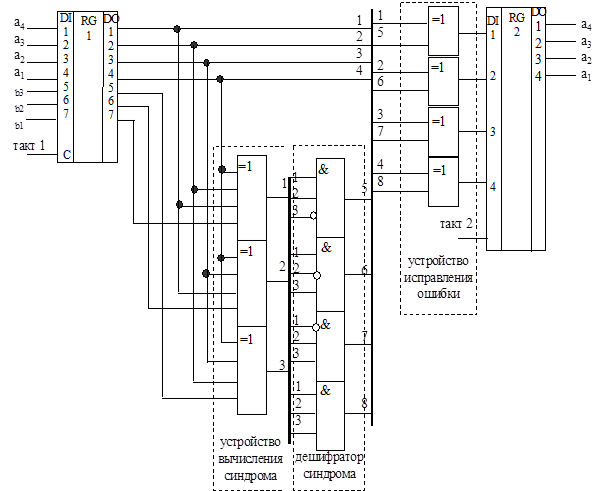
Синтезированная на основе этих рассуждений функциональная схема декодера приведена на рис. 7.2.

Рис.7.2. Декодер систематического кода (7,4)

Декодер, работающий в режиме обнаружения ошибок, проще, поскольку

в нем отсутствует устройство исправления ошибок, а дешифратор синдрома может быть заменен одной схемой (рис. 7.3.) выявления ненулевого синдрома.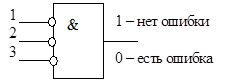
Рис. 7.3. Схема выявления ненулевого синдрома

Контрольные вопросы к лабораторной работе №7 [1. с. 148-163]

7-1. Что называется кодированием в широком смысле?

7-2. Что называется алфавитом источника?

7-3. Что называется объемом алфавита источника?

7-4. Что называется кодированием в узком смысле?

7-5. Что называется кодовой комбинацией?

7-6. Что называется кодом?

7-7. Что называется основанием кода?

7-8. Какой код называется равномерным?

7-9. чем продиктована необходимость замены каждого символа источника совокупностью кодовых символов?

7-10. Какие комбинации кода называются разрешенными?

7-11. Что называется мощностью кода?

7-12. Что является численной характеристикой избыточности кода?

7-13. Какой код называется безизбыточным?

7-14. Почему безизбыточные коды не обладают помехоустойчивостью?

7-15. Какое кодирование называется помехоустойчивым?

7-16. Какие коды называются кодами с обнаружением ошибок?

7-17. Какие коды называются кодами с обнаружением ошибок?

7-18. Что называется кодовым расстоянием между двумя кодовыми комбинациями?

7-19. Какую операцию необходимо выполнить для определения кодового расстояния между двумя кодовыми комбинациями?

7-20. Что называется кодовым расстоянием кода?

7-21. Что называется вектором ошибки?

7-22. Что называется кратностью ошибки?

7-23. Перечислите параметры биномиального закона распределения кратности ошибок?

7-24. Как связаны кодовое расстояние кода и вероятность ошибочного декодирования?

7-25. Как связаны кодовое расстояние кода и кратность обнаруживаемых им ошибок?

7-26. Как связаны кодовое расстояние кода и кратность исправляемых им ошибок?

7-27. Какой избыточный код называется блоковым?

7-28. Какой избыточный код называется разделимым?

7-29. Какой разделимый избыточный код называется систематическим?

7-30. Почему большинство систематических разделимых кодов называются линейными?

7-31. Что называется спектром кода?

7-32. Что является характерной особенностью кодов, называемых циклическими?

7-33. Чему равна мощность кода на одно сочетание?

7-34. Как осуществляется декодирование кода на одно сочетание?

7-35. Является ли код на одно сочетание разделимым?

7-36. Как осуществляется декодирование кода с проверкой паритета?

7-37. Как определяется коэффициент избыточности для разделимых равномерных двоичных кодов?

7-38. Как осуществляется декодирование кода с простым повторением?

7-39. Как осуществляется декодирование инверсного кода?

7-40. Как осуществляется декодирование корреляционного кода?

7-41. На что указывает граница Хемминга?

7-42. На что указывает граница Плоткина?

7-43. На что указывает граница Варшамова - Гилберта?

7-44. Почему систематические линейные коды называются групповыми?

7-45. В чем состоит свойство замкнутости группы?

7-46. Как определяются значения контрольных разрядов в каждой кодовой комбинации группового линейного систематического кода?

7-47. Что является особенностью группового линейного систематического кода?

7-48. Чем определяется число проверочных уравнений для группового систематического кода?

7-49. Что задает система проверочных уравнений группового систематического кода?

7-50. Какие кодовые комбинации называются образующими или базисными векторами для того или иного группового линейного кода?

7-51. Почему в качестве образующих удобно выбрать комбинации, которые содержать лишь по одной единице в информационных разрядах?

7-52. Как формируется образующая матрица (n,k)-кода, если задана система проверочных уравнений?

7-53. Как при наличии образующей матрицы можно найти все остальные кодовые комбинации (n,k)-кода?

7-54. Из каких подматриц состоит образующая матрица (n,k)-кода?

7-55. Как может быть сформирована дополняющая матрица (n,k)-кода, если не заданы проверочные уравнения?

7-56. Как, пользуясь образующей матрицей (n,k)-кода, построить систему проверочных уравнений?

7-57. Как, пользуясь образующей матрицей (n,k)-кода, построить проверочную матрицу?

7-58. Как, пользуясь проверочной матрицей (n,k)-кода, построить систему проверочных уравнений?

7-59. Что называется синдромом?

7-60. Какое значение синдрома указывает на наличие ошибки в принятой кодовой комбинации?

7-61. Что называется исправляющим вектором?

7-62. Как можно истолковать содержимое дополняющей подматрицы, пользуясь понятием синдрома?

7-63. Как можно истолковать содержимое единичной подматрицы, пользуясь понятием синдрома?

7-64. Как осуществляется декодирование по максимуму правдоподобия?

7-65. Какие (n,k)-коды называются кодами Хэмминга?

7-66. Что называется радиусом сферической упаковки кода?

7-67. Что называется радиусом покрытия кода?

7-68. Какой код называется совершенным?

7-69. Какой код называется квазисовершенным?

7-70. Как осуществляется укорочение кода?

7-71. Как сказывается укорочение кода на размерах образующей матрицы?

7-72. Как сказывается укорочение кода на размерах проверочной матрицы?

7-73. С какой целью выполняется укорочение кода?

7-74. Как осуществляется расширение кода?

7-75. Как сказывается расширение кода на размерах образующей матрицы?

7-76. Как сказывается расширение кода на размерах проверочной матрицы?

7-77. С какой целью выполняется расширение кода?

7-78. Как образуется расширенный код Хэмминга (8,4) с d=4?

7-79. Как определяется отсутствие ошибок в принятой кодовой комбинации расширенного кода Хэмминга (8,4) с d=4?

7-80. Как определяется наличие двух ошибок в принятой кодовой комбинации расширенного кода Хэмминга (8,4) с d=4?