Методические указания по выполнению лабораторной работы № 5

Манипулированный сигнал представляет собой несущее гармоническое колебание, один из параметров которого (амплитуда – АМ, фаза – ФМ, частота - ЧМ) меняется во времени по закону модулирующих прямоугольных импульсов.

Если нормированные манипулирующие импульсы 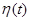изменяются в пределах 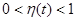, то модулированный сигнал запишется при АМ

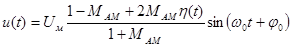, (5.1)

при ФМ

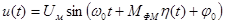, (5.2)

при ЧМ

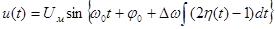. (5.3)

В формулах (5.1 – 5.3) используются следующие обозначения:

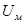- амплитуда манипулированного сигнала;

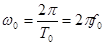- круговая частота несущей;

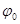- начальная фаза несущей;

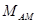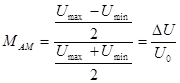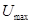- коэффициент амплитудной модуляции, который равен отношению полуразмаха модулированного сигнала к его среднему значению , где - максимальное значение амплитуды модулированного сигнала, 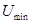- минимальное значение амплитуды модулированного сигнала, 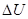- максимальное приращение амплитуды модулированного сигнала относительно амплитуды несущей 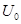, тогда ;

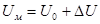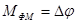- индекс модуляции при ФМ;

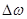- девиация частоты, т.е. величина максимального отклонения мгновенной частоты от частоты несущей при ЧМ.

Для получения спектров манипулированных сигналов нет необходимости разлагать их в ряд Фурье. Достаточно знать разложение в ряд Фурье манипулирующих импульсов 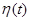, которое затем подставляется в приведенные выше формулы. Периодическая последовательность прямоугольных импульсов с длительностью 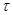и периодом повторения 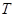при 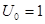(условие нормировки) может быть представлена рядом Фурье

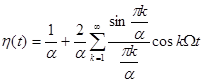, (5.4)

где 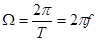- круговая частота манипулирующей последовательности; 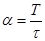- отношение периода повторения манипулирующей последовательности к длительности импульса, называемое скважностью импульсной последовательности.

Для получения выражения описывающего спектр сигнала при амплитудной манипуляции следует подставить выражение (5.4) в формулу (5.1). После подстановки и группирования членов получим выражение

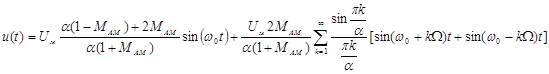, (5.5)

в котором для упрощения без потери общности принято, что начальная фаза несущей .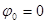

Формула (5.5) показывает, что в состав спектра амплитудно-манипулированного сигнала кроме несущей с частотой 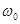входят верхняя и нижняя боковые полосы частот. Компоненты верхней боковой полосы имеют частоты 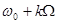, а компоненты нижней боковой полосы – частоты 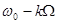. Амплитуда компонент зависит от коэффициента модуляции 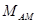и скважности 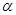манипулирующей последовательности. В формуле (5.5) символ 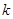обозначает номера боковых гармоник ( ).

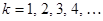Таким образом, амплитуда несущей гармоники

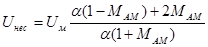, (5.6)

а амплитуды боковых гармоник

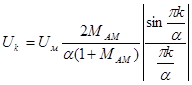. (5.7)

При заданных параметрах несущей и параметрах манипулирующей импульсной последовательности с помощью формул (5.6) и (5.7) при изменении 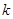в заданных пределах могут быть построены спектральные диаграммы сигнала манипулированного по амплитуде.

Используя простые тригонометрические преобразования и полагая для упрощения 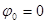, сигнал при фазовой модуляции согласно выражению (5.2) можно записать в виде

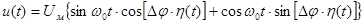. (5.8)

Таким образом, для нахождения спектра сигнала модулированного по фазе достаточно найти спектры функци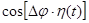й и 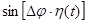. Этот метод пригоден при любом способе фазовой модуляции.

Однако для случая фазовой манипуляции, когда фаза изменяется скачком, можно воспользоваться более простым и наглядным методом.

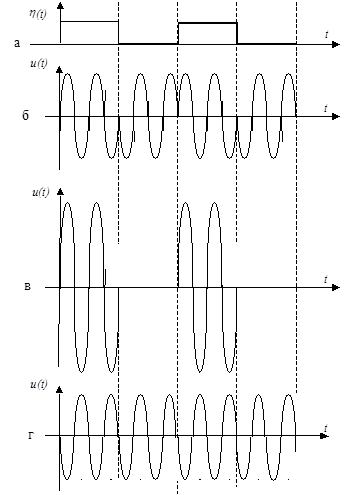
На рис. 5.1 показано, что при манипулирующем сигнале (рис. 5.1а) и использовании фазовой манипуляции со скачком фазы на 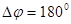, манипулированный сигнал (рис. 5.1б) можно рассматривать как сумму сигнала, манипулированного по амплитуде с вдвое большей амплитудой (рис. 5.1в) и немодулированного колебания (рис. 5.1г), фаза которого противоположна фазе несущей этого сигнала, манипулированного по амплитуде.
Рис. 5.1. Фазовая манипуляция

Эту закономерность можно обобщить на случай любой величины фазового скачка 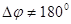. Следовательно, фазовую манипуляцию на угол 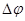можно рассматривать как сумму АМ сигнала и немодулированной несущей.

Отсюда можно сделать вывод о том, что спектр сигнала, манипулированного по фазе, аналогичен по форме со спектром сигнала, манипулированного по амплитуде, за исключением несущей.

С учетом этого амплитуда несущей гармоники может быть найдена из выражения

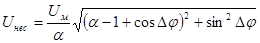, (5.9)

а амплитуды боковых гармоник

. (5.10)

При заданных параметрах несущей и параметрах манипулирующей импульсной последовательности с помощью формул (5.9) и (5.10) при изменении 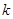в заданных пределах могут быть построены спектральные диаграммы сигнала манипулированного по фазе.

Если фазовая модуляция производится не скачком, то спектр необходимо вычислять более сложным путем – по общей формуле (5.8). В этом случае спектр сигнала, модулированного по фазе, перестает быть аналогичным по форме спектру сигнала, модулированного по амплитуде.

При передаче дискретных сообщений используются методы двукратной (ДФМ) и трехкратной (ТФМ) фазовой манипуляции. Абсолютная величина скачков фазы может иметь при ДФМ два значения (например, и 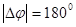), а при ТФМ – четыре значения (например, 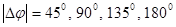). В том случае, когда чередуются скачки фаз разной величины, приведенные выше формулы также перестают быть справедливыми. Спектр таких сигналов существенно изменяется и может быть несимметричным относительно несущей частоты.

При частотной манипуляции скачком происходит изменение частоты относительно исходной частоты немодулированной несущей. Изменение частоты производится при постоянной амплитуде сигнала и без разрывов фаз.

Если в выражении (5.3) для частотной модуляции положить 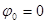и обозначить 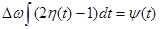, назвав ее переходной фазой, то после тригонометрических преобразований выражение (5.3) можно записать

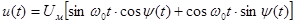. (5.11)

Таким образом, для нахождения спектра сигнала, модулированного по частоте, надо найти спектры функци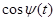й и 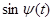. Этот метод пригоден при любом способе частотной модуляции.

В простейшем частном случае частотной манипуляции при скважности 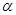манипулирующих импульсов равной двум частота скачком изменяется через равные промежутки времени от нижней частоты 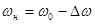к верхней частоте 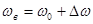и обратно. Для этого случая легко найти, что переходная фаза будет изменяться по пилообразному закону. Разложив функци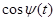й и 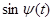, можно из приведенных ранее выражений получить формулы для амплитуд спектральных составляющих. Амплитуда несущей получается равной

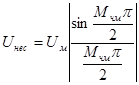, (5.12)

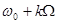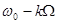амплитуды нечетных боковых составляющих (верхних и нижних) с частотами соответственно и при 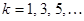равны

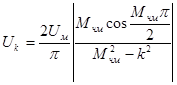, (5.13)

а амплитуды четных боковых при равны

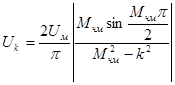, (5.14)

где 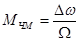- индекс частотной модуляции, равный отношению девиации частоты 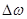к частоте 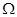повторения манипулирующей последовательности.

Из приведенных формул видно, что форма спектра сильно зависит от индекса частотной модуляции. При увеличении индекса частотной модуляции количество боковых гармоник, имеющих заметную амплитуду, возрастает.

Еще больше спектр усложняется, если скважность манипулирующих импульсов не равна двум. В этом случае спектр становится несимметричным относительно несущей частоты.

Рассмотрение спектров модулированных и манипулированных сигналов позволяет заметить, что методы модуляции можно разделить на две группы.

В первой группе зависимость между модулирующим и модулированным сигналами выражается простой функцией, благодаря чему спектр боковой полосы модулированного сигнала имеет такую же форму, как спектр модулирующего сигнала. Таким свойством обладает амплитудная модуляция и фазовая манипуляция. Эти методы можно назвать линейными.

Во второй группе зависимость между модулирующим и модулированным сигналами выражается сложной функцией. Спектр модулированного сигнала не похож на спектр модулирующего сигнала. Так обстоит дело при частотной и фазовой модуляции. Эти методы называются нелинейными.

Контрольные вопросы к лабораторной работе №5 [1. с. 90-109]

5-1. Что служит математической моделью несущей при модуляции?

5-2. Для чего служат идентифицирующие параметры несущей?

5-3. Для чего служат информативные параметры несущей?

5-4. Какой процесс называется модуляцией?

5-5. В чем состоит основное назначение модуляции?

5-6. Какие методы модуляции называются непрерывными?

5-7. Какие методы модуляции называются угловой модуляцией?

5-8. Что называется коэффициентом или глубиной амплитудной модуляции?

5-9. Какие составляющие содержит спектр сигнала при амплитудной модуляции гармонической несущей гармоническим модулирующим сигналом?

5-10. От чего зависит амплитуда боковых при амплитудной модуляции гармонической несущей гармоническим модулирующим сигналом?

5-11. Каким образом можно построит спектр модулированного сигнала при амплитудной модуляции гармонической несущей произвольным модулирующим сигналом с известным спектром?

5-12. Чему равна полоса частот напряжения, модулированного по амплитуде?

5-13. Какой вид модуляции называется манипуляцией?

5-14. Почему при амплитудной манипуляции следует говорить лишь о практически необходимой ширине спектра манипулированного сигнала?

5-15. В чем состоят недостатки использования для передачи АМ-сигнала с двумя боковыми?

5-16. Какое преимущество обеспечивает применение АМ-ОБП?

5-17. Какое преимущество обеспечивает подавление несущей при передаче АМ-сигнала?

5-18. В чем состоит недостаток применения АМ-ОБП с подавлением несущей?

5-19. Что называется девиацией частоты при частотной модуляции?

5-20. Что называется индексом частотной модуляции?

5-21. Какова теоретическая ширина спектра ЧМ-сигнала?

5-22. Как практически необходимая ширина спектра ЧМ-сигнала зависит от индекса частотной модуляции?

5-23. Какую частотную модуляцию называют узкополосной?

5-24. Какую частотную модуляцию называют широкополосной?

5-25. Чему равна практически необходимая ширина спектра при широкополосной частотной модуляции?

5-26. В чем состоит основное преимущество широкополосной ЧМ?

5-27. Что называется индексом фазовой модуляции?

5-28. В чем состоит принципиальное отличие ЧМ и ФМ?

5-29. От чего зависит индекс фазовой модуляции?

5-30. Как выглядит спектр сигнала манипулированного по фазе?

5-31. Какое явление называется обратной работой?

5-32. Чем ОФМ отличается от ФМ?

5-33. Какая ОФМ называется многократной?

5-34. Как может быть образован манипуляционный элемент при использовании ДОФМ или ТОФМ?

5-35. В чем состоят преимущества применения ДОФМ или ТОФМ?

5-36. Какие параметры несущей манипулируются при использовании КАМ?

5-37. Что называется сигнальным созвездием?

5-38. Сколько бит содержит манипуляционный элемент при использовании КАМ-16?

5-39. Как с помощью сигнальных созвездий можно сравнивать различные виды модуляции по помехоустойчивости?

Лабораторная работа № 6

Помехоустойчивость приема единичных элементов при различных видах модуляции