Методические указания по выполнению лабораторной работы № 8
Из полиномиального описания циклических кодов следует, что процессы кодирования и декодирования этих кодов представляют собой операции деления полиномов. Для аппаратной реализации операции деления полиномов используются циклические регистры сдвига, т.е. последовательные регистры с обратной связью, в цепи которой устанавливаются сумматоры по модулю два.
Один из методов построения кодера циклического кода на основе упомянутых регистров можно описать следующим образом:
1. Число разрядов регистра, т.е. число триггеров, выбирается равным числу проверочных разрядов n-k, т.е. равным степени образующего полинома.
2. Число двухвходовых сумматоров по модулю два берется на единицу меньше числа членов образующего полинома.
3. Триггеры регистра нумеруются слева направо от 1 до n-k.
| Таблица 8.1. Варианты заданий | |||
| № вар. | Описание кода | № вар. | Описание кода |
Образующий полином  .
Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига. .
Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
| Образующий полином 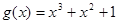 .
Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига. .
Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
| ||
Проверочный полином  . Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига. . Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
| Проверочный полином 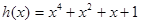 . Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига. . Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
| ||
Каноническая образующая матрица
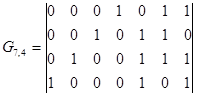 Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
| Каноническая образующая матрица
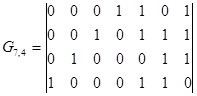 Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
| ||
Неканоническая образующая матрица
 Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
| Неканоническая образующая матрица
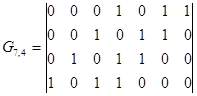 Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
| ||
Система проверочных уравнений
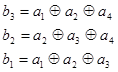 Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
Синтезировать функциональную схему кодера на основе (n-k)-разрядного регистра сдвига.
| Система проверочных уравнений
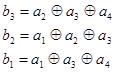 Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
Синтезировать функциональную схему кодера на основе k-разрядного регистра сдвига.
|
4. Сумматоры по модулю два располагаются после тех триггеров, номера которых совпадают со степенями ненулевых членов образующего полинома.
5. Выходы предыдущих триггеров соединяются со входами последующих через сумматоры по модулю два там, где они есть, или непосредственно, там где их нет.
6. На второй вход сумматора по модулю два, первый вход которого соединен с выходом последнего триггера с номером n-k, подаются в последовательном коде информационные разряды, т.е. этот вход является входом кодера. Выход этого сумматора соединяется с входом первого триггера и вторыми входами всех остальных сумматоров по модулю два.
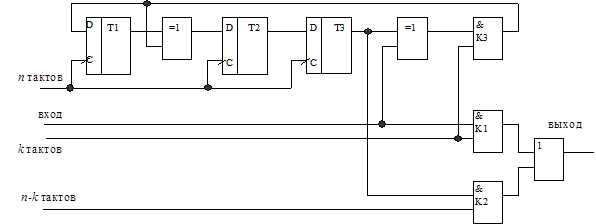
После того, как все k информационных разрядов последовательно поступят в кодер, будучи одновременно выданными в линию, в триггерах регистра будет сформирован остаток, состоящий из n-k контрольных символов, которые должны быть переданы вслед за информационными. Для управления этим процессом в структуру кодера необходимо ввести три ключа К1, К2, К3. Ключи К1 и К2 необходимы для того, чтобы коммутировать выход кодера либо с входом кодера при передаче k информационных разрядов, либо с выходом регистра при передаче n-k контрольных разрядов. Чтобы эти уже сформированные разряды выдвигались из регистра без искажений, необходимо разорвать цепь обратной связи, для чего и служит ключ К3. Синтезированная с учетом сказанного структура кодера циклического кода (7,4) с образующим полиномом g(x)=x3+x+1 приведена на рис. 8.1.
|
| Рис. 8.1. Кодер циклического кода (7,4) |
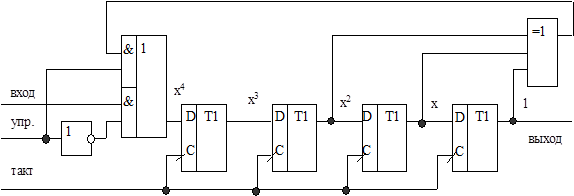
Иногда более удобной оказывается другая реализация кодера с использованием не (n-k)-разрядного, а k-разрядного регистра сдвига с обратной связью на основе сумматоров по модулю два, который описывается не образующим, а т.н. проверочным полиномом h(x), получаемым в соответствии с выражением 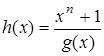 . Работа кодера начинается с того, что в регистр с отключенной обратной связью заносятся k информационных символов. Затем обратная связь включается, и регистр сдвигается n раз. Первые k символов, поступающие с выхода кодера, являются информационными, следующие за ними (n-k) символов – контрольными. Построенная в соответствии с этим полиномом структура кодера будет выглядеть так, как показано на рис. 8.2. Разметка регистра сдвига кодера осуществляется в соответствии с проверочным полиномом.
. Работа кодера начинается с того, что в регистр с отключенной обратной связью заносятся k информационных символов. Затем обратная связь включается, и регистр сдвигается n раз. Первые k символов, поступающие с выхода кодера, являются информационными, следующие за ними (n-k) символов – контрольными. Построенная в соответствии с этим полиномом структура кодера будет выглядеть так, как показано на рис. 8.2. Разметка регистра сдвига кодера осуществляется в соответствии с проверочным полиномом.
|
| Рис. 8.2. Кодер циклического кода (7,4) |
Декодер циклического кода в соответствии с изложенным ранее принципом декодирования содержит устройство деления полинома принятой кодовой комбинации на образующий полином. Это устройство реализуется так же, как и в кодере с помощью циклического регистра сдвига с сумматорами по модулю два, расставленными между триггерами регистра в соответствии с образующим полиномом. Отличие декодера состоит в том, что цепь обратной связи берется не с выхода последнего сумматора, а с выхода последнего триггера регистра. Кроме того, в состав декодера необходимо ввести буферный регистр для хранения информационных разрядов и дешифратор остатка (синдрома).
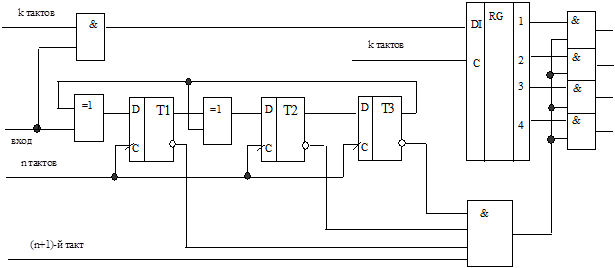
Дешифратор остатка может быть реализован по-разному в зависимости от того, в каком режиме используется данный код: только для обнаружения ошибок или для исправления ошибок. В случае работы в режиме обнаружения ошибок дешифратор остатка только выявляет, равен остаток нулю или не равен. Если остаток не равен нулю, то вырабатывается сигнал о наличии ошибки в принятой комбинации и запрещается передача хранящихся в буферном регистре информационных разрядов для дальнейшей обработки. С учетом этого структуру такого декодера можно представить следующим образом (рис. 8.3).
|
| Рис. 8.3. Декодер циклического кода (7,4) в режиме обнаружения ошибки |
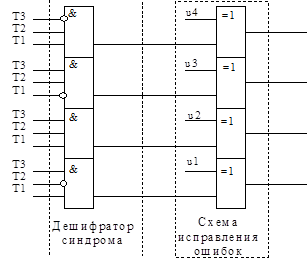
Для построения декодера с исправлением одиночной ошибки в него необходимо включить дешифратор синдрома, построенный в соответствии с образующей матрицей, и аналогичную использованной ранее (рис. 7.2) схему исправления ошибок (рис. 8.4).
|
| Рис. 8.4. Дополнение схемы декодера для режима исправления ошибки |
Контрольные вопросы к лабораторной работе №8 [1. с. 164-193]
8-1. Как можно записать кодовую комбинацию в виде полинома?
8-2. Какой полином называется порождающим полиномом кода?
8-3. Что называется полем Галуа?
8-4. Как определяются мультипликативная и аддитивная единицы поля Галуа?
8-5. Как определяются обратный элемент по сложению и обратный элемент по умножению для поля Галуа?
8-6. При каком числе элементов существуют конечные алгебраические поля?
8-7. Какое конечное алгебраическое поле называется простым?
8-8. Какое конечное алгебраическое поле называется расширенным?
8-9. Как выполняется операция сложения кодовых полиномов?
8-10. Как выполняется операция умножения кодовых полиномов?
8-11. Как выполняется операция деления кодовых полиномов?
8-12. Какие коды называются циклическими?
8-13. Как при полиномиальном представлении осуществляется процесс формирования кодовой комбинации циклического кода?
8-14. Какими свойствами должен обладать образующий полином циклического кода?
8-15. Как может быть построена каноническая образующая матрица циклического кода, если задан образующий полином?
8-16. Как может быть построена неканоническая образующая матрица циклического кода, если задан образующий полином?
8-17. Как из неканонической формы образующей матрицы получить каноническую форму?
8-18. Что играет роль синдрома при декодировании циклических кодов?
8-19. Что представляют собой операции кодирования и декодирования при полиномиальном представлении циклических кодов?
8-20. Какие устройства используются для аппаратной реализации операций деления полиномов?
8-21. При каких условиях возможно применение метода мажоритарного декодирования?
8-22. Какая система проверочных уравнений называется ортогональной?
8-23. В чем состоит суть метода мажоритарного декодирования?
8-24. Какие параметры являются исходными при кодировании с помощью БЧХ-кодов?
8-25. Что представляет собой образующий полином БЧХ-кода?
8-26. Какие коды называются кодами максимальной длины?
8-27. Что называется пакетом ошибок?
Дата добавления: 2015-07-30; просмотров: 1252;
