Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности

Действие равномерно распределенной нагрузки [38] в условиях пространственной задачи возникает тогда, когда к поверхности линейно деформируемого полупространства приложена местная нагрузка, распределенная по площади квадрата, прямоугольника, круга, эллипса и др. Значения вертикальных сжимающих напряжений σ_z в любой точке полупространства от действия нагрузки интенсивностью р, равномерно распределенной по площади прямоугольника размером l x b, были впервые получены А. Лявом. Практический интерес представляют значения сжимающих напряжений , проведенных из центра σ_zО и из углов σ_zС загруженной площади (рис. 3).

,

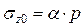где α – определяется по прил. К, в зависимости от величин n = l/b и
m = 2·z/b (l – длинная сторона, b – короткая сторона прямоугольника загружения, z – расстояние от точки до поверхности приложения нагрузки).

,

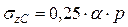где α – определяется по прил. Л, в зависимости от величин n = l/b и
m = z/b.

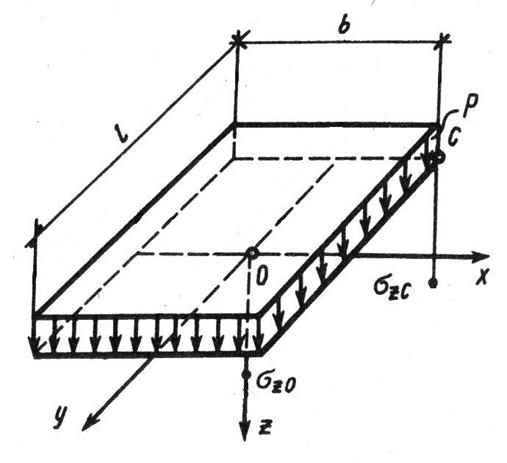
Рис. 3. Расчетная схема для определения сжимающих напряжений

под центром и под углом прямоугольника с равномерно распределенной нагрузкой

Для определения сжимающих напряжений в любой точке полупространства М применяют метод угловых точек, используя формулу

.

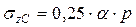На рис. 4 представлены различные варианты расположения точки М. В методе угловых точек всегда принимают l ≥ b.

На рис. 4 а и б точка М расположена в пределах площади загружения. Для этих случаев площадь загрузки разбивают, соответственно, на два и четыре прямоугольника так, чтобы точка М была угловой точкой для каждого из них. Тогда напряжение σ_zМ находят суммированием напряжений под угловыми точками площадей загружения. Соответственно для первого и второго случаев

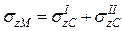и .

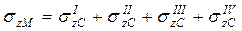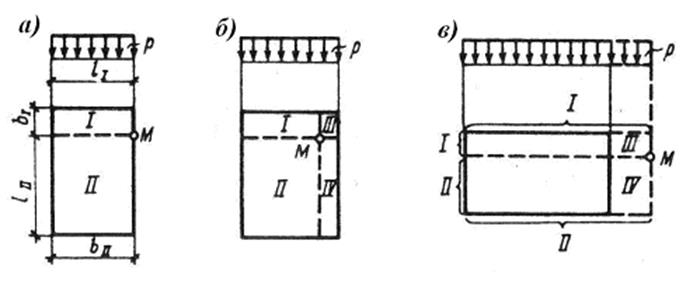
Рис. 4. Схема для расчета напряжений методом угловых точек

На рис. 4 в точка М расположена вне пределов площади загружения. Для данного случая точку М можно представить как угловую точку фиктивных площадей загружения I и II, при этом в пределах площадей III и IV фиктивная нагрузка прикладывается в обратном направлении. Напряжение σ_zМ определяется по выражению

.

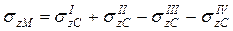Пример 4. Определить напряжение в точке М от распределенной нагрузки, интенсивностью р = 2 кг/см², при b = 1,5 м, l = 3 м, z = 3 м, а₁ = а₂ = 1,5 м. Расчетная схема представлена на рис. 5 а.

По методу угловых точек загруженную площадь делим на два прямоугольника таким образом, чтобы точка М попадала в угол каждого из них (рис. 5 а).

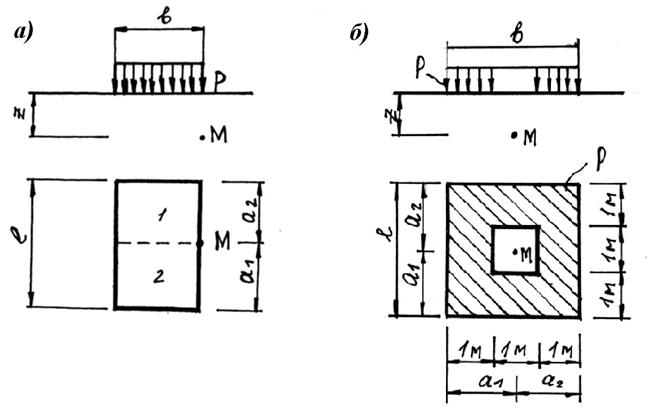
Рис. 5. Расчетные схемы

Далее определяем коэффициенты α для каждого из прямоугольников как функцию значений n и m (прил. Л), учитывая, что прямоугольник 1 и прямоугольник 2 равны (рис. 5 а).

.

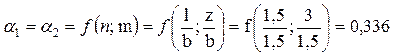Напряжение в точке М определяем как сумму напряжений от прямоугольников 1 и 2, учитывая, что эти прямоугольники равны (рис. 5 а).

кг/см².

Пример 5. Определить напряжение в точке М от распределенной нагрузки, интенсивностью р = 2 кг/см², при b = 3 м, l = 3 м, z = 3 м, а₁ = а₂ = 1,5 м. Расчетная схема представлена на рис. 5 б.

Точка М находится под центром большого (загруженного) и малого (незагруженного) прямоугольников (рис. 5 б).

Далее определяем коэффициенты α для большого и малого прямоугольников как функцию значений n и m (прил. Л).

,

.

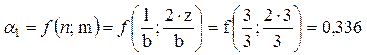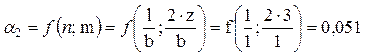Напряжение в точке М, определяем как разность напряжений большого прямоугольника (с фиктивной загрузкой от малого прямоугольника) и малого прямоугольника (фиктивной загрузки) (рис. 5 б):

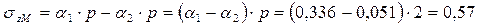кг/см².

3. Определение напряжений в массиве грунта
от действия собственного веса (бытовое давление)

На практике используют упрощенную методику расчета, основанную на предположении о том, что природные напряжения в массиве грунта формируются только под действием собственного веса [3  8]. Также принято считать, что все деформации массива от собственного веса прекратились и напряжения полностью стабилизировались.Практический интерес представляют значения сжимающих напряжений σ_z.

При горизонтальной поверхности массива грунта однородного напластования сжимающие напряжения на глубине z определяются выражением

,

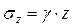где γ – удельный вес грунта.

Эпюра природных напряжений массива грунта однородного напластования при горизонтальной поверхности будет иметь вид треугольника (рис. 6 а).

При неоднородном напластовании или наличии подземных вод, а также при горизонтальной поверхности напряжения от собственного веса грунтов будут определяться отдельно для каждого слоя (рис. 6 б). Причем удельный вес грунта, расположенного ниже уровня подземных вод, будет определяться с учетом взвешивающего действия воды γ_sb:

,

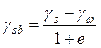где γ_s – удельный вес частиц грунта; γ_ω – удельный вес воды, принимается равным 1 т/м³; е – коэффициент пористости грунта.

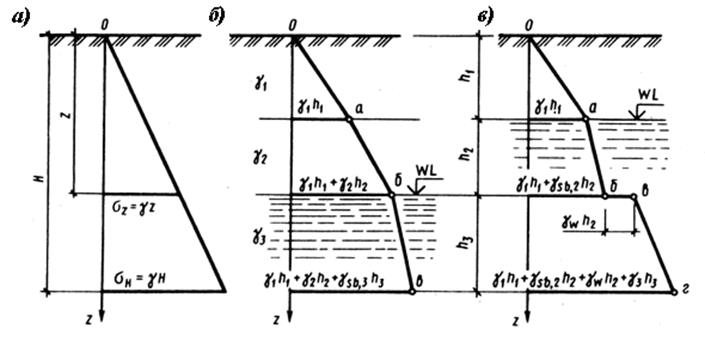
Рис. 6. Эпюры распределения напряжений от собственного веса грунтов

Если ниже уровня подземных вод залегает водоупорный слой, то на его кровле дополнительно учитывают давление от столба вышерасположенной воды равное γ_ω·h_ω (рис. 6 в).

Пример 6. Определить напряжения от собственного веса грунтов и построить эпюру распределения данных напряжений по скважине № 1. Исходные данные см. примеры 1 и 2.

Первоначально на основании данных инженерно-геологических изысканий (см. пример 2) строим в масштабе геологическую колонку с указанием мощности слоев грунта, уровней подземных вод и водоупора (рис. 7). Далее на основании результатов определения физико-механических характеристик грунтов (см. пример 1) для каждого слоя грунта указываем необходимые для дальнейшего расчета данные.

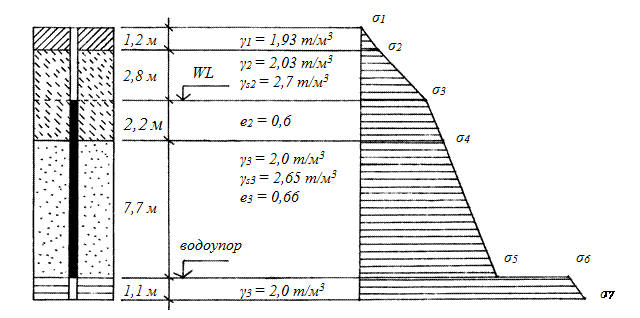Рис. 7. Совмещенная схема геологической колонки и эпюры

распределения напряжений от собственного веса грунтов

Расчет напряжений от собственного веса грунтов проводим последовательно, начиная от поверхности земли. Расчетные точки располагаем на поверхности земли, на границах слоев грунтов, на уровнях подземных вод и водоупора.

На поверхности земли дополнительная пригрузка отсутствует, поэтому напряжение равно .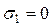

Напряжение на границе между первым и вторым слоями грунта определяем как сумму напряжений σ₁ и от собственного веса грунта первого слоя:

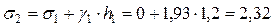т/м³.

Напряжение на уровне подземных вод определяем как сумму напряжений σ₂ и от собственного веса грунта второго слоя на расстоянии от его кровли до уровня подземных вод:

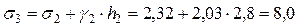т/м³.

Напряжение на границе между вторым и третьим слоями грунта определяем как сумму напряжений σ₃ и от собственного веса грунта второго слоя на расстоянии от уровня подземных вод до его подошвы, при этом учитываем взвешивающее действие воды на частицы грунта второго слоя

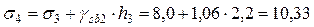т/м³,

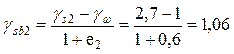где т/м³.

Напряжение на границе между третьим и четвертым слоями грунта определяем как сумму напряжений σ₄ и от собственного веса грунта третьего слоя, при этом учитываем взвешивающее действие воды на частицы грунта третьего слоя

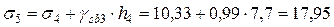т/м³,

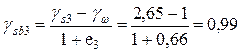где т/м³.

На кровле четвертого слоя напряжение определяем с учетом дополнительного напряжения от столба вышерасположенной воды как сумму напряжений σ₅ и от собственного веса столба вышерасположенной воды:

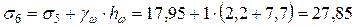т/м³.

На уровне нижней границы скважины напряжение определяем как сумму напряжений σ₆ и от собственного веса грунта четвертого слоя на расстоянии от его кровли до уровня забоя скважины:

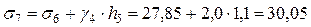т/м³.

Далее по полученным значениям σ₁–σ₇ в масштабе строим эпюру распределения напряжений от собственного веса грунтов, которую совмещаем с уже построенной геологической колонкой (рис. 7).