Матрицы. Операции над матрицами
Прямоугольной матрицей размера ( 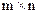 ) называется совокупность
) называется совокупность 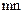 чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде
чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде
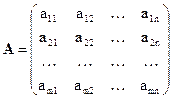 (4.1)
(4.1)
или сокращенно в виде 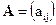
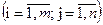 . Числа
. Числа 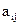 , составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы
, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы 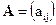 и
и 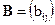 одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть
одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть 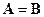 , если
, если 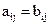 .
.
Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.
Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера 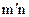 , все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть
, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть 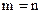 , то матрицу называют квадратной порядка
, то матрицу называют квадратной порядка 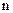 . Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:
. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:
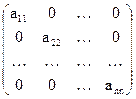 .
.
Если все элементы 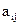 диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой
диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой 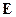 :
:
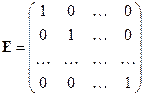 .
.
Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком 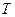 наверху.
наверху.
Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу
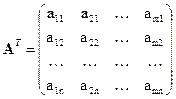 ,
,
которая будет транспонированной по отношению к матрице 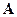 . В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
Произведением матрицы 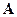 на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы
на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы 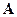 умножением на число l:
умножением на число l: 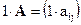 .
.
Суммой двух матриц 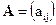 и
и 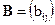 одного размера называется матрица
одного размера называется матрица 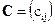 того же размера, элементы которой определяются по формуле
того же размера, элементы которой определяются по формуле 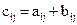 .
.
Произведение 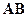 матрицы
матрицы 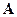 на матрицу
на матрицу 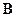 определяется в предположении, что число столбцов матрицы
определяется в предположении, что число столбцов матрицы 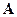 равно числу строк матрицы
равно числу строк матрицы 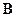 .
.
Произведением двух матриц 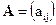 и
и 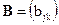 , где
, где 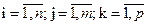 , заданных в определенном порядке
, заданных в определенном порядке 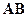 , называется матрица
, называется матрица 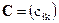 , элементы которой определяются по следующему правилу:
, элементы которой определяются по следующему правилу:
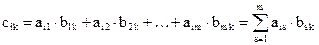 . (4.2)
. (4.2)
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы 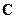 равен сумме произведений элементов i-й строки матрицы
равен сумме произведений элементов i-й строки матрицы 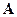 на соответствующие элементы k-го столбца матрицы
на соответствующие элементы k-го столбца матрицы 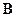 .
.
Пример 2.1. Найти произведение матриц 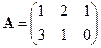 и
и 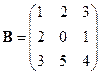 .
.
Решение. Имеем: матрица 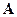 размера
размера 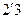 , матрица
, матрица 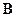 размера
размера 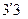 , тогда произведение
, тогда произведение 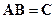 существует и элементы матрицы
существует и элементы матрицы 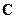 равны
равны
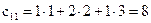 ,
,  ,
, 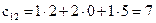 ,
,
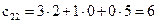 ,
, 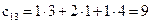 ,
, 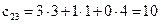 .
.
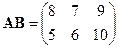 , а произведение
, а произведение 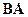 не существует.
не существует.
Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины 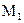 ,
,  и
и 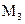 , причем доставка единицы продукции с каждого молокозавода в магазин
, причем доставка единицы продукции с каждого молокозавода в магазин 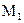 стоит 50 ден. ед., в магазин
стоит 50 ден. ед., в магазин  ‑ 70, а в
‑ 70, а в 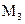 ‑ 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
‑ 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
| 
| 
| |
Решение. Обозначим через 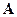 матрицу, данную нам в условии, а через
матрицу, данную нам в условии, а через 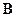 ‑ матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
‑ матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
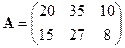 ,
, 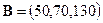 .
.
Тогда матрица затрат на перевозки будет иметь вид:
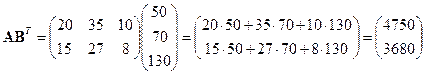 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй ‑ 3680 ден.ед.
Пример 2.3. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором 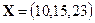 . Используются ткани четырех типов
. Используются ткани четырех типов 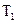 ,
, 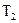 ,
, 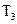 ,
, 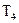 . В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор
. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор 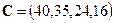 задает стоимость метра ткани каждого типа, а вектор
задает стоимость метра ткани каждого типа, а вектор 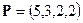 ‑ стоимость перевозки метра ткани каждого вида.
‑ стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
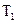
| 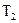
| 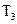
| 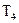
| |
| Зимнее пальто | ||||
| Демисезонное пальто | ||||
| Плащ |
1. Сколько метров ткани каждого типа потребуется для выполнения плана ?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Решение. Обозначим через 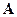 матрицу, данную нам в условии, т. е.,
матрицу, данную нам в условии, т. е.,
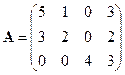 ,
,
тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор 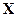 умножить на матрицу
умножить на матрицу 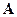 :
:
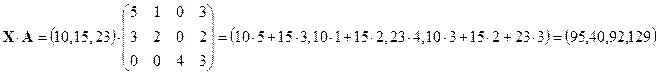 Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу 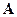 и вектор
и вектор 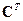 :
:
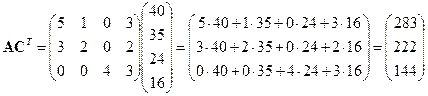 .
.
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
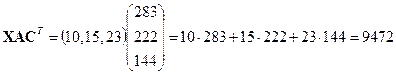
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
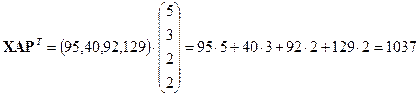 .
.
Итак, 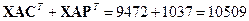 X (ден. ед).
X (ден. ед).
Дата добавления: 2015-07-30; просмотров: 765;
