Приближенные методы расчета температурных режимов при эксплуатации породных теплообменников

Если принять, что вода, фильтрующая в породном теплообмен­нике, нагревается только за счет тепла, заключенного в его объеме, а потеря тепла в нем компенсируется за счет подпитки теплообмен­ника теплом из окружающих пород, то при самом первом приближе­нии, в соответствии с уравнением теплового баланса имеем

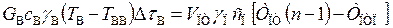(1.36)

где G_в — объемный расход воды, фильтрующей через породный теплообменник, м³/с;

с_b — удельная теплоемкость воды, Дж/ (кг • К);

γ_в— плотность воды, кг/м³;

Т_в - средняя температура воды на выходе из породного теплобменника за время очередного п-го интервала эксп­луатации породного теплообменника, К;

Т_ВB — средняя температура воды на входе в породный теплообменик за время п-го интервала эксплуатации, К;

Δτ_п = Δτ₁ = Δτ₂ = Δτ₃ ... — равные интервалы эксплуатации породно­го теплообменника, с;

Vпт — объем раздробленных пород породного теплообмен­ника, м³;

γ_п — плотность пород породного теплообменника, кг/м³;

c_п— удельная теплоемкость пород теплообменника, Дж/(кг-К);

Тпт(п-1) — средняя температура пород в породном теплооб­меннике за время (п-1)-го интервала его эксплуа­тации, К;

Т_ПТП — средняя температура пород в породном теплооб­меннике за время п-го интервала его эксплуата­ции, К.

При высокой степени разрыхления породного массива в объеме теплообменника можно считать температуру воды на выходе из теп­лообменника, равной температуре его пород, т.е.

Т_в ⁼ Т_пт.

С учетом этого, выражение (1.36) можно представить в виде:

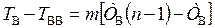
откуда

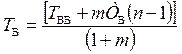(1.37)

где

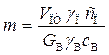(1.38)

Для самого первого интервала эксплуатации породного теплообменника температура воды на выходе из него будет равна

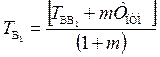(1.39)

где Твв₁ — температура воды на входе в породный теплообменник в самом начале его эксплуатации, К; Т_пто — начальная температура пород в породном теплообмен­нике, К.

Формулы (1.36)-(1.38) являются довольно приближенными, од­нако они позволяют качественно оценить влияние расхода воды и объема породного теплообменника на температуру теплоносителя. Более точные формулы, но тоже приближенные, можно получить, если учитывать условия теплообмена в породном теплообменнике, силы гравитации и трения. С учетом этого для начального периода эксплуатации породного теплообменника (от нескольких дней до нескольких месяцев) дифференциальное уравнение теплового баланса на участке продольной зоны дробления можно записать в виде

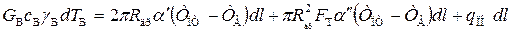(1.40)

где Т_в — температура воды на выходе из породного теплообмен­ника, К;

R_ДP — радиус продольной (вдоль скважины) зоны дробления, м;

Т_ПT — температура пород в породном теплообменнике, К;

l — переменная длина продольной зоны дробления породно­го теплообменника, м;

Fт — суммарная теплообменная поверхность кусков горной породы в 1 м³ породного теплообменника, м /м ;

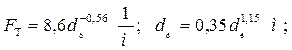(1.41)

d_к — средний приведенный диаметр куска горной породы, м; 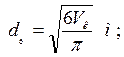V_к — средний объем куска горной породы, м³; α' — коэффициент нестационарного теплообмена между по­родным теплообменником и окружающим его массивом, Вт/(м²К);

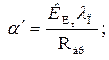(1.42)

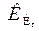— критерий Кирпичева;

λ_П — теплопроводность пород, Вт/(м·К);

α"- коэффициент нестационарного теплообмена между теплоносителем и раздробленными породами породного те­плообменника, Вт/(м·К);

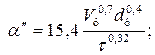(1.43)

V_ф — скорость фильтрации теплоносителя в породном теплообменнике, м/с;

τ — время эксплуатации породного теплообменника, час;

q_пн — тепловыделение от потерь напора теплоносителя на еди­нице длины скважины в единицу времени, Дж/ (м с);

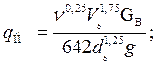(1.44)

ν - кинематическая вязкость теплоносителя, для воды при

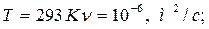
g — ускорение свободного падения, g = 9,81 м/с .

Левая часть выражения

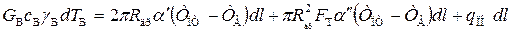
представляет собой теплопроизводительность породного теплообменника. Первое слагаемое правой части характеризует теплопроизводительность породного теплооб­менника за счет его теплообмена с окружающим массивом, второе - за счет теплообмена внутри породного теплообменника, третье — за счет тепловыделения от гидравлических потерь в фильтрационных каналах.

Приведем дифференциальное уравнение (1.40) к виду

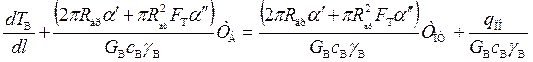
Полученное уравнение является линейным неоднородным уравнением первого порядка и его решение, найдем по формуле Эйлера

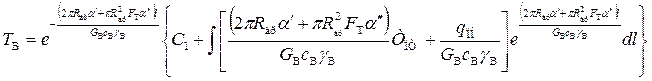после интегрирования и алгебраических преобразований общее решение принимает вид

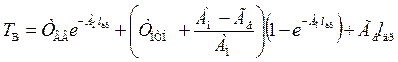(1.45)

где Т_в — температура воды на выходе из породного теплообменника, К;

Т_вв — температура воды на входе в породный теплообмен­ник, К;

Т_ПТП — температура пород в начале (по ходу движения воды) породного теплообменника, К;

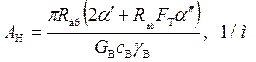; (1.46)

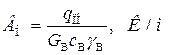; (1.47)

l_др — длина зоны дробления породного теплообменника, м; Г_е — градиент температуры по длине породного теплообмен­ника, К/м; если отводящая скважина пробурена под углом β к вертикальной нагнетательной скважине, то

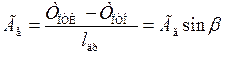(1.48)

а если нагнетательная скважина состыковывается с отводящей путем искривления ствола последней с постоянным радиусом кривизны R_КP то

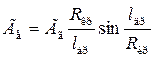(1.49)

В последнем случае

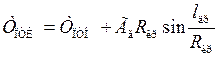(1.50)

где Т_птк — температура пород в конце (по ходу движения воды) породного теплообменника, К;

Г_г — геотермический градиент, К/м.

Для больших значений времени эксплуатации породных тепло­обменников (годы и десятки лет) дифференциальное уравнение теп­лового баланса имеет вид

(1.51)

где R_с — радиус скважины, м;

τ — время эксплуатации скважины, с.

Уравнение (1.51) легко приводится к линейному неоднородному дифференциальному уравнению первого порядка, поэтому его решение имеет вид

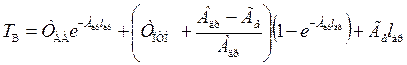(1.52)

где

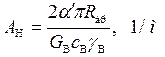; (1.53)

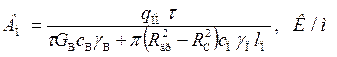(1.54)

При времени эксплуатации породного теплообменника τ > 5÷10 лет и при достаточно большом расходе воды вторым слага­емым в знаменателе последнего выражения можно пренебречь. В этом случае

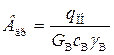(1.55)

ТЕМА №2. ПРОМЕРЗАНИЕ СВЯЗНЫХ ПОРОД ПРИ ОТКРЫТОЙ РАЗРАБОТКЕ МЕСТОРОЖДЕНИЙ