Закон сохранения времени ожидания
При изменении дисциплины обслуживания время ожидания заявок в очередях сокращается для одних типов заявок за счет увеличения времени ожидания заявок других типов. Для систем с одним обслуживающим прибором выполняется закон сохранения времени ожидания, который состоит в следующем: для любой дисциплины обслуживания
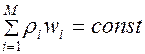 (2)
(2)
где 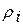 - загрузка прибора, wi - среднее время ожидания в очереди заявок типа
- загрузка прибора, wi - среднее время ожидания в очереди заявок типа
i = 1, …, M.
Закон (2) справедлив, если система отвечает следующим требованиям:
1. отсутствуют отказы в обслуживании,
2. система обслуживания простаивает лишь в том случае, если на ее входе нет заявок на обслуживание,
3. при наличии прерываний длительность обслуживания описывается экспоненциальным распределением,
4. все входные потоки описываются независимыми пуассоновскими распределениями, и длительность обслуживания не зависит от входных потоков.
Закон сохранения времени ожидания можно использовать для оценки достоверности приближенных результатов, полученных при анализе сложных дисциплин обслуживания.
Лекция. Характеристики дисциплин обслуживания
Характеристики бесприоритетных дисциплин обслуживания
При бесприоритетной дисциплине заявки разных типов не имеют заранее определенных привилегий на первоочередное обслуживание. Это правило выполняется, если заявки на обслуживание выбираются:
1) в порядке поступления; 2) в порядке, обратном порядку поступления; 3) наугад, т.е. путем случайного выбора из очереди.
Дисциплина обслуживания в порядке поступления называется FIFO, а дисциплина обслуживания в обратном порядке – LIFO. Указанные три бесприоритетные дисциплины характеризуются одинаковым средним временем ожидания заявок, но дисциплина FIFO минимизирует дисперсию времени ожидания, т.е. уменьшает разброс времени ожидания относительно среднего значения.
Бесприоритетное обслуживание на основе дисциплины FIFO организуется в соответствии со схемой:

 z1
z1
О












 z2 Пр
z2 Пр


 .
.
.
.
 zm
zm
где Пр - это процессор , О - очередь заявок типа z1,…, zM.
Вновь поступившая заявка заносится в конец очереди. Заявки выбираются на обслуживание из начала очереди. Пусть в систему поступают заявки М типов с интенсивностями λ1,…,λM.Предположим, что каждый из входных потоков заявок – пуассоновский. Тогда суммарный поток заявок также пуассоновский и его интенсивность
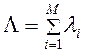 (3)
(3)
Пусть известны также математические ожидания 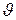 1, …,
1, …, 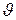 M и вторые начальные моменты
M и вторые начальные моменты 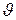 1(2), …,
1(2), …, 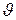 M(2) времени обслуживания заявок типа 1, …, М. Эти значения характеризуют распределение времени выполнения соответствующих программ. Второй начальный момент – среднее значение квадрата случайной величины. Тогда при использовании бесприоритетной дисциплины обслуживания среднее время ожидания заявок всех типов одинаково и равно:
M(2) времени обслуживания заявок типа 1, …, М. Эти значения характеризуют распределение времени выполнения соответствующих программ. Второй начальный момент – среднее значение квадрата случайной величины. Тогда при использовании бесприоритетной дисциплины обслуживания среднее время ожидания заявок всех типов одинаково и равно:
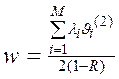 (4)
(4)
Выразим второй начальный момент через коэффициент вариации 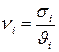 - отношение среднеквадратичного отклонения длительности обслуживания
- отношение среднеквадратичного отклонения длительности обслуживания 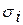 к его математическому ожиданию.
к его математическому ожиданию.
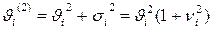
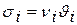

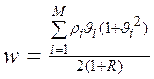 (4/)
(4/)
где R = 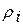 + …..+
+ …..+ 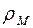 <1 – суммарная загрузка системы.
<1 – суммарная загрузка системы.
Из (4/)видно, что среднее время ожидания заявок в очереди минимально при постоянной длительности обслуживания заявок каждого типа ( 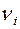 =0) и увеличивается по мере роста дисперсии времени обслуживания. Среднее время ожидания существенно зависит от общей загрузки R процессора. При R→1, w→+∞, т.е. заявки могут ожидать обслуживания сколь угодно долго.
=0) и увеличивается по мере роста дисперсии времени обслуживания. Среднее время ожидания существенно зависит от общей загрузки R процессора. При R→1, w→+∞, т.е. заявки могут ожидать обслуживания сколь угодно долго.
При экспоненциальном распределении длительности обслуживания функция распределения времени ожидания заявок в очереди:
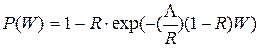 (5)
(5)
При W=0 P(W) определяет вероятность того, что в момент поступления очередной заявки процессор свободен:
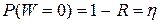 .
.

Время пребывания заявки типа i = 1, …, M в системе 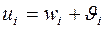 . Посколько при бесприоритетном обслуживании время ожидания заявок всех типов одинаково (все
. Посколько при бесприоритетном обслуживании время ожидания заявок всех типов одинаково (все 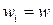 ), то
), то 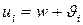 . Таким образом, при одинаковом времени ожидания время пребывания в системе заявок разных типов различно.
. Таким образом, при одинаковом времени ожидания время пребывания в системе заявок разных типов различно.
Характеристики дисциплины обслуживания с относительными приоритетами заявок
Если требуется, чтобы заявки некоторого типа имели меньшее время ожидания, чем заявки других типов, то необходимо первым предоставить преимущественное право на обслуживание, называемое приоритетом. Приоритеты заявок характеризуются целыми положительными числами 1,2,3…, причем более высокому приоритету соответствует меньшее число. Если приоритеты учитываются только в момент выбора заявки на обслуживание, то их называют относительными. Относительность приоритета связана со следующим. В момент выбора сравниваются приоритеты ожидающих заявок и обслуживание предоставляется заявке с наиболее высоким приоритетом. После этого выбранная заявка захватывает процессор. Если в процессе обслуживания данной заявки поступают заявки с более высокими приоритетами, то процесс обслуживания данной заявки не прекращается, т.е. эта заявка, захватив процессор, оказывается наиболее приоритетной. Этот возникший приоритет относителен: он имеет место только после захвата процессора. При использовании относительных приоритетов обработка заявок организуется по следующей схеме:
O1









 z1
z1
O2 Zi










 z2 Пр
z2 Пр

 .
.
.. ОМ






 zМ dfg
zМ dfg

Заявкам типа z1, …, zM присвоены относительные приоритеты 1, …, М соответственно. Поступившая в систему заявка 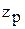 (p=1, ..., M) заносится в очередь
(p=1, ..., M) заносится в очередь 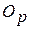 , в которой хранятся заявки приоритета p. В очереди заявки упорядочены по времени поступления. Когда процессор заканчивает обслуживание некоторой заявки, то управление передается программе Диспетчер. Диспетчер выбирает на обслуживание заявку с наибольшим приоритетом, а именно заявку zi, если очереди O1, …, Oi-1 не содержат заявок. Выбранная заявка захватывает процессор на все время обслуживания.
, в которой хранятся заявки приоритета p. В очереди заявки упорядочены по времени поступления. Когда процессор заканчивает обслуживание некоторой заявки, то управление передается программе Диспетчер. Диспетчер выбирает на обслуживание заявку с наибольшим приоритетом, а именно заявку zi, если очереди O1, …, Oi-1 не содержат заявок. Выбранная заявка захватывает процессор на все время обслуживания.
Если в систему поступает М простейших потоков с интенсивностями λ1, …, λM и длительности обслуживания заявок каждого потока имеют мат. ожидания 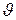 1, …,
1, …, 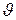 M и вторые начальные моменты
M и вторые начальные моменты 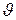 1(2), …,
1(2), …, 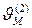 соответственно, то среднее время ожидания в очереди заявок приоритета k = 1, … , M, определяется по формуле:
соответственно, то среднее время ожидания в очереди заявок приоритета k = 1, … , M, определяется по формуле:
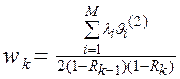 k=1,…,.M (6)
k=1,…,.M (6)
где Rk-1 = 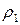 +…..+
+…..+ 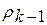 ; Rk =
; Rk = 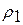 +….+
+….+ 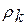 - суммарные загрузки процессора потоками заявок z1, …,zk-1 и z1, …, zkсоответственно.
- суммарные загрузки процессора потоками заявок z1, …,zk-1 и z1, …, zkсоответственно.
Используя коэффициенты вариации длительности обслуживания, выражение (6) можно представить в виде:
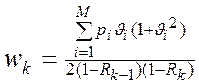 (6/)
(6/)
Проанализируем соотношение между временами ожидания заявок с разными приоритетами. При увеличении значения приоритета к=1…М-1 на единицу среднее время ожидания (6) изменяется на
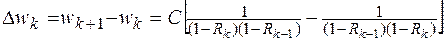 ,
,
где -положительный коэффициент, не зависящий от k.
-положительный коэффициент, не зависящий от k.
После преобразований получаем
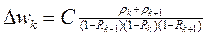 .
.
Т.к. Ri<1, то 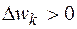 ,откуда следует, что
,откуда следует, что 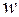 1<
1< 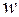 2<….
2<…. 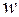 M . Таким образом, времена ожидания заявок монотонно увеличиваются с уменьшением приоритета.
M . Таким образом, времена ожидания заявок монотонно увеличиваются с уменьшением приоритета.
Теперь сопоставим время ожидания заявок, имеющих относительные приоритеты 1, …, М, с временем ожидания при бесприоритетном обслуживании. Из формул (6) и (4) видно, что времена ожидания различаются постольку, поскольку различаются величины 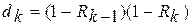 и (1-R)в знаменателях соответствующих выражений.
и (1-R)в знаменателях соответствующих выражений.
Т.к. 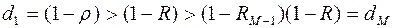 , то
, то 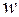 1<
1< 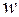 <
< 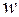 M,
M,
где 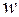 - среднее время ожидания заявок при бесприоритетном обслуживании, причем
- среднее время ожидания заявок при бесприоритетном обслуживании, причем 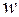 1<
1< 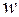 2<….
2<…. 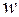 M. Сл-но, введение относительных приоритетов приводит к уменьшению времени ожидания заявок с высокими приоритетами и увеличению времени ожидания заявок с низкими приоритетами по сравнению с бесприоритетным обслуживанием.
M. Сл-но, введение относительных приоритетов приводит к уменьшению времени ожидания заявок с высокими приоритетами и увеличению времени ожидания заявок с низкими приоритетами по сравнению с бесприоритетным обслуживанием.




 k
k 
FIFO

ОП
 1
1





 к
к
1  M
M
Характеристики дисциплины обслуживания с абсолютными приоритетами
В ряде случаев время ожидания заявок некоторых типов нужно уменьшить в такой степени, которая недостижима при использовании относительных приоритетов. Предполагается, что время ожидания существенно уменьшится, если при поступлении высокоприоритетной заявки обслуживание ранее поступившей заявки с низшим приоритетом прерывается и процессор тут же предоставляется для обслуживания высокоприоритетной заявки. Дисциплина обслуживания, при которой высокоприоритетная заявка прерывает обслуживание заявки с низким приоритетом, называется дисциплиной обслуживания с абсолютными приоритетами. При использовании абсолютных приоритетов обслуживание заявки осуществляется по следующей схеме:



 О1
О1














 z1
z1



 О2 zi
О2 zi














 z2 Пр
z2 Пр


 .
.
 .
.
 . ОМ
. ОМ


















 .
.

 ZМ
ZМ
 2
2
1- заявка, ожидающая обслуживания
2- прерванная заявка
Для каждого потока заявок 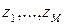 организуется очередь
организуется очередь 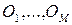 , в которой заявки размещаются в порядке поступления. Заявкам
, в которой заявки размещаются в порядке поступления. Заявкам 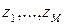 соответствуют абсолютные приоритеты 1, …, М. Если процессор занят обслуживанием заявки
соответствуют абсолютные приоритеты 1, …, М. Если процессор занят обслуживанием заявки 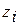 и на вход поступает заявка
и на вход поступает заявка 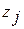 , то при
, то при  заявка
заявка 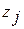 заносится в конец очереди
заносится в конец очереди 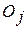 , а при
, а при 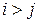 обслуживание заявки
обслуживание заявки 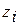 прерывается, заявка
прерывается, заявка 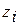 заносится в начало очереди
заносится в начало очереди 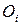 и Диспетчер переключает процессор на обслуживание заявки
и Диспетчер переключает процессор на обслуживание заявки 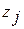 .
.
Обслуживание прерванных заявок может проводиться: 1) от начала; 2) от момента прерывания (дообслуживание). По возможности стремятся использовать 2-й способ.
Если длительность обслуживания распределена по экспоненциальному закону, среднее время дообслуживания совпадает со средним временем обслуживания заявки.
Если потоки заявок - простейшие с интенсивностями 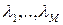 и мат. ожидания и 2-е начальные моменты длительности обслуживания равны соответственно
и мат. ожидания и 2-е начальные моменты длительности обслуживания равны соответственно 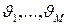 и
и 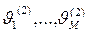 и прерванная заявка дообслуживается от точки прерывания, то среднее время ожидания заявки с абсолютным приоритетом k(k = 1, …, М), определяется следующим образом:
и прерванная заявка дообслуживается от точки прерывания, то среднее время ожидания заявки с абсолютным приоритетом k(k = 1, …, М), определяется следующим образом:
 (7)
(7)
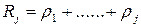 – загрузка системы от первых j потоков заявок.
– загрузка системы от первых j потоков заявок.
Сопоставление формул (7) и (6) показывает, что при обслуживании с абсолютными приоритетами длительность ожидания заявок k-го приоритета изменяется на величину
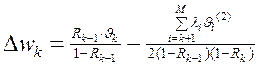 ,
,
где первое слагаемое определяет влияние заявок более высокого приоритета, прерывающих обслуживание заявок данного приоритета, а второе слагаемое учитывает уменьшение времени ожидания заявок k-го приоритета за счет прерываний обслуживания заявок с меньшими приоритетами. Из этого выражения можно определить условие, при котором длительность ожидания в очереди заявок k-го приоритета при наличии прерываний будет меньше, чем длительность ожидания при обслуживании с относительными приоритетами, т.е. условие, при котором 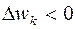 имеет вид:
имеет вид:
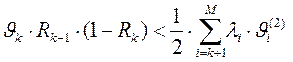
Эффект от использования абсолютных приоритетов иллюстрирует рисунок:
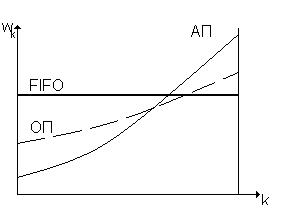
где ОП – кривая относительного приоритета , АП – кривая абсолютного приоритета.
Присваивание заявкам абсолютных приоритетов приводит к уменьшению времени ожидания заявок с высокими приоритетами, но одновременно с этим увеличивается время ожидания низкоприоритетных заявок.
Дата добавления: 2015-07-30; просмотров: 2373;
