Характеристики ЦУС при одномерном потоке заявок
Одной из важнейших характеристик качества функционирования ЦУС является загрузка:
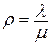 (1)
(1)
где λ- интенсивность поступления заявок в систему, μ- интенсивность обслуживания заявок.
Заменяя в формуле (1) 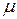 величиной
величиной 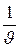 , получим
, получим 
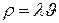 . Значение
. Значение 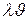 определяет среднее число заявок, поступающих в систему за среднее время
определяет среднее число заявок, поступающих в систему за среднее время 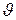 обслуживания одной заявки. Наряду с этим величина загрузки характеризует долю времени, в течении которого обслуживающий прибор занят обслуживанием заявок, и одновременно вероятность того, что в произвольный момент времени обслуживающий прибор работает (не простаивает). Покажем это. Пусть рассматриваемая система функционирует в течение достаточно большого периода времени T. За время T в систему поступит
обслуживания одной заявки. Наряду с этим величина загрузки характеризует долю времени, в течении которого обслуживающий прибор занят обслуживанием заявок, и одновременно вероятность того, что в произвольный момент времени обслуживающий прибор работает (не простаивает). Покажем это. Пусть рассматриваемая система функционирует в течение достаточно большого периода времени T. За время T в систему поступит 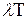 заявок, которые будут обслужены за время
заявок, которые будут обслужены за время 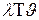 , где
, где 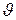 - средняя длительность обслуживания. Тогда доля времени, в течение которого система была занята обслуживанием заявок,
- средняя длительность обслуживания. Тогда доля времени, в течение которого система была занята обслуживанием заявок,
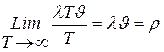
Поскольку загрузка 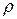 - вероятность того, что система работает, то вероятность простоя определяется значением:
- вероятность того, что система работает, то вероятность простоя определяется значением:
 – коэффициент простоя
– коэффициент простоя
При этом предполагается, что ρ<1, что справедливо для всех реальных систем.
Все время работы системы можно разделить на два интервала: интервал переходного режима работы системы от момента начала работы до момента входа в стационарный режим и интервал стационарного режима.
Стационарным или установившемся режимом называется такой режим работы, при котором вероятностные характеристики функционирования системы не изменяются во времени. Условие существования стационарного режима определяется значением загрузки 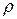 <1. Если
<1. Если 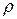 >1, т.е. интенсивность поступления заявок превышает интенсивность обслуживания, то работа системы характеризуется неограниченным возрастанием длины очереди заявок перед обслуживающим прибором, т.е. не существует стационарного режима работы системы. Случай
>1, т.е. интенсивность поступления заявок превышает интенсивность обслуживания, то работа системы характеризуется неограниченным возрастанием длины очереди заявок перед обслуживающим прибором, т.е. не существует стационарного режима работы системы. Случай 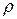 =1 требует особого рассмотрения.
=1 требует особого рассмотрения.
Качество функционирования ЦУС определяется временем пребывания заявок в системе 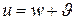 , где
, где 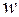 - время ожидания заявки в очереди,
- время ожидания заявки в очереди, 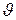 - время обслуживания заявки в процессоре. В общем случае:
- время обслуживания заявки в процессоре. В общем случае:
w=wн+wп
где 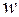 н - время ожидания начала обслуживания, равное интервалу времени от момента поступления заявки в систему до момента, когда заявка первый раз принимается на обслуживание,
н - время ожидания начала обслуживания, равное интервалу времени от момента поступления заявки в систему до момента, когда заявка первый раз принимается на обслуживание, 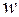 п - время ожидания в прерванном состоянии, связанное с прерыванием обслуживания данной заявки и ожиданием дальнейшего обслуживания. Если обслуживание заявки не прерывается, то
п - время ожидания в прерванном состоянии, связанное с прерыванием обслуживания данной заявки и ожиданием дальнейшего обслуживания. Если обслуживание заявки не прерывается, то 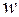 п =0 и
п =0 и 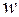 =
= 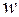 н .
н .
С изменением дисциплины обслуживания время обслуживания 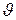 не изменяется. Наряду с временем пребывания заявки в системе как характеристику качества функционирования ЦУС можно использовать время ожидания заявки в очереди w. Именно для этой характеристики получено большинство аналитических результатов. Рассмотрим остальные характеристики обслуживания заявок, такие как средняя длина очереди и среднее число заявок в системе.
не изменяется. Наряду с временем пребывания заявки в системе как характеристику качества функционирования ЦУС можно использовать время ожидания заявки в очереди w. Именно для этой характеристики получено большинство аналитических результатов. Рассмотрим остальные характеристики обслуживания заявок, такие как средняя длина очереди и среднее число заявок в системе.
Для систем с неограниченным ожиданием, когда поступившая заявка ожидает в очереди обслуживания сколь угодно долго, не покидая систему, средняя длина очереди 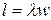 , где
, где 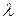 - интенсивность поступления заявок в систему. Это выражение очевидно, если учесть, что за время ожидания w в очереди одной заявки в среднем поступает
- интенсивность поступления заявок в систему. Это выражение очевидно, если учесть, что за время ожидания w в очереди одной заявки в среднем поступает 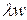 заявок, которые ожидают в очереди начала обслуживания.
заявок, которые ожидают в очереди начала обслуживания.
Аналогичными рассуждениями можно получить выражение для среднего числа заявок в системе:
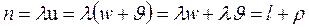 .
.
В данном случае загрузка 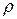 рассматривается как среднее число заявок, обслуживаемых в процессоре ЦУС. Действительно, в процессоре в каждый момент времени с вероятностью
рассматривается как среднее число заявок, обслуживаемых в процессоре ЦУС. Действительно, в процессоре в каждый момент времени с вероятностью 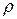 находится одна заявка на обслуживании и с вероятностью 1-
находится одна заявка на обслуживании и с вероятностью 1- 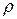 - нуль заявок (процессор простаивает). Поэтому среднее число заявок, обслуживаемых в процессоре, равно
- нуль заявок (процессор простаивает). Поэтому среднее число заявок, обслуживаемых в процессоре, равно 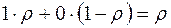 .
.
Дата добавления: 2015-07-30; просмотров: 719;
