Характеристики дисциплин обслуживания со смешанными приоритетами
В некоторых системах необходимо выполнить жесткие ограничения на время ожидания отдельных заявок, что требует присваивания им абсолютных приоритетов. В результате этого время ожидания низкоприоритетных заявок может оказаться недопустимо большим. Чтобы выполнить ограничения по всем типам заявок, можно наряду с абсолютными приоритетами некоторым заявкам присвоить относительные приоритеты, а остальные заявки обслуживать без приоритетов. Такая дисциплина называется смешанной.
Дисциплина обслуживания с несколькими классами приоритетов
Пусть в систему поступает M типов заявок. Если заявки обслуживаются без приоритетов (дисциплина FIFO), то для заявок типа 1,…, М1 срдеднее время ожидания может оказаться недопустимо большим (рис. а). Если перейти к дисциплине с относительными приоритетами (кривая ОП), то для заявок типа 1, …, М1 положение исправляется, но времена ожидания заявок с низкими приоритетами превышают предельно допустимые значения.
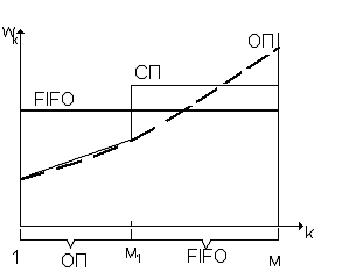
а)
Если заявкам типа 1, …, М1 присвоить относительные приоритеты, а заявки типа М1+1, …, М обслуживать без приоритетов, то среднее время ожидания соответствует кривой СП (рис. а) и, возможно, удовлетворяет заданным ограничениям.
Случаи использования других смешанных дисциплин обслуживания показаны на рисунках б) и в).
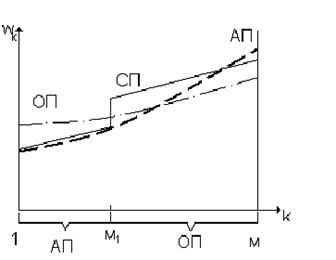 б)
б)
 в)
в)
Рассмотрим смешанную дисциплину обслуживания с 3-мя классами заявок, когда заявкам типа 1,…, М1, присваиваются абсолютные приоритеты, заявкам типа М1+1, …, М1+М2 - относительные приоритеты, заявки типа М1+М2+1, …, М обслуживаются в соответствии с бесприоритетной дисциплиной.
В i - ом классе находится Мi типов заявок. М – общее число типов заявок в системе. Будем иметь в виду, что все заявки первого класса обладают абсолютным приоритетом по отношению к заявкам 2-го и 3-го классов и все заявки 2 – го класса – относительным приоритетом по отношению к заявкам 3 – го класса. Определим средние времена ожидания заявок различных типов.
Для заявок 1–го класса с абсолютными приоритетами характерна независимость среднего времени ожидания от характеристик обслуживания заявок с более низким приоритетом, поэтому среднее время ожидания заявки 1- го класса будет таким же, как и при использовании чистой дисциплины обслуживания с абсолютными приоритетами, т.е. будет определяться формулой (7).
Заявки 2 и 3 – го классов могут рассматриваться как заявки с относительными приоритетами, время ожидания которых увеличено за счет прерывания заявками 1- го класса, причем заявки 3 – го класса обладают самым низким относительным приоритетом. Таким образом, среднее время ожидания заявок этих классов можно представить:
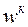 =
= 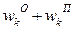 ,
,
где 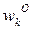 - среднее время ожидания заявок с относительными приоритетами без учета прерываний со стороны заявок 1 – го класса;
- среднее время ожидания заявок с относительными приоритетами без учета прерываний со стороны заявок 1 – го класса;
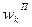 - среднее время ожидания, вызванное прерыванием рассматриваемой заявки k заявками типа 1, …, М1, относящимися к 1- му классу.
- среднее время ожидания, вызванное прерыванием рассматриваемой заявки k заявками типа 1, …, М1, относящимися к 1- му классу.
По аналогии с выражением (7): 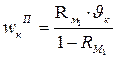 ,
,
где 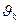 - среднее время обслуживания заявки типа k = M1+1, …, М,
- среднее время обслуживания заявки типа k = M1+1, …, М,
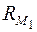 =
= 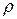 1 + …+
1 + …+ 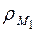 - загрузка системы со стороны заявок 1- го класса.
- загрузка системы со стороны заявок 1- го класса.
Для заявок 2 – го класса величина  будет определяться формулой (6):
будет определяться формулой (6):
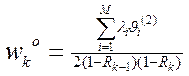
После преобразований это же выражение может быть использовано и для заявок 3 – го класса. В связи с этим отметим, что в знаменателе 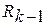 - загрузка со стороны всех заявок более высокого относительного приоритета, чем рассматриваемая заявка, а величина
- загрузка со стороны всех заявок более высокого относительного приоритета, чем рассматриваемая заявка, а величина  - загрузка со стороны заявок более высокого приоритета, включая рассматриваемую заявку типа k. Поскольку заявки 3 – го класса рассматриваются как заявки с самым низким относительным приоритетом, т.е. заявки типа 1, …, M1+M2 обладают более высоким приоритетом, то загрузка со стороны этих заявок:
- загрузка со стороны заявок более высокого приоритета, включая рассматриваемую заявку типа k. Поскольку заявки 3 – го класса рассматриваются как заявки с самым низким относительным приоритетом, т.е. заявки типа 1, …, M1+M2 обладают более высоким приоритетом, то загрузка со стороны этих заявок:

Загрузка с учетом заявок 3 – го класса представляет собой суммарную загрузку системы :
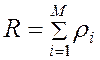
Таким образом для заявок 3 – го класса величина среднего времени ожидания

Т. е. для системы со смешанными приоритетами с 3 – мя классами заявок среднее время ожидания заявок разных типов определяется следующим образом:

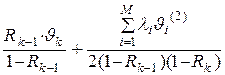 , k = 1, …, М.
, k = 1, …, М.
 =
= 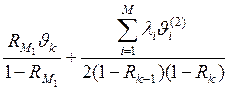 , k = М1+1, …, М1+М2
, k = М1+1, …, М1+М2
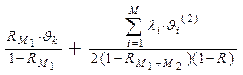 , k = M1+M2+1, ..., M
, k = M1+M2+1, ..., M
Из рассмотренной дисциплины обслуживания со смешанными приоритетами и 3 – мя классами заявок могут быть получены как частные случаи простейшей дисциплины: с абсолютными приоритетами (М2 = М3 = 0), с относительными приоритетами (М1 = М3 = 0), бесприоритетная дисциплина (М1 = М2 = 0), а также смешанные дисциплины с 2 – мя классами заявок: с абсолютными и относительными приоритетами (М3 = 0), с абсолютными приоритетами и без приоритетов (М2 = 0), с относительными приоритетами и без приоритетов (М1 = 0).
Дата добавления: 2015-07-30; просмотров: 958;
