Понятие несобственного интеграла
Несобственным интегралом 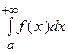 от функции
от функции 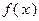 на полуинтервале
на полуинтервале 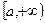 называется предел функции
называется предел функции 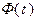 при
при 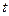 , стремящемся к
, стремящемся к 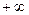 , т.е.
, т.е.
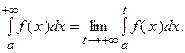
Если предел, стоящий в правой части равенства, существует и конечен, то несобственный интеграл называется сходящимся(к данному пределу), в противном случае – расходящимся. Работая с несобственными интегралами, обычно выделяют две задачи:
- исследование вопроса о сходимости заданного несобственного интеграла;
- вычисление значения интеграла в случае, если он является сходящимся.
Пример 6.4.Вычислить 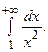
Решение.По определению 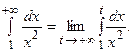
Для нахождения интеграла, стоящего под знаком предела, используем формулу Ньютона – Лейбница:
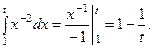
Тогда
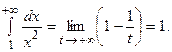
Таким образом, искомый несобственный интеграл сходится к 1.
Если рассматривать несобственный интеграл на интервале 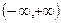 , то его можно представить как сумму двух интегралов, т.е.
, то его можно представить как сумму двух интегралов, т.е.
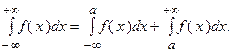
Если интегралы, входящие в правую часть равенства, сходятся, то рассматриваемый интеграл называется сходящимся, а если хотя бы один из интегралов правой части расходится, то – расходящимся.
Пример 6.5.Вычислить 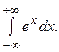
Представим интеграл в виде суммы двух интегралов и исследуем их на сходимость, полагая 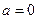 .
.
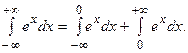
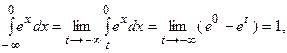 т.е. первый интеграл сходится к 1.
т.е. первый интеграл сходится к 1.
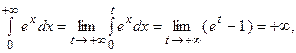 т.е. второй интеграл расходится, а, следовательно, расходящимся будет и несобственный интеграл
т.е. второй интеграл расходится, а, следовательно, расходящимся будет и несобственный интеграл 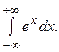
Вычислить несобственные интегралы (или установить их расходимость):
6.34. 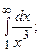 6.35.
6.35. 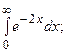
6.36. 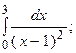 6.37.
6.37. 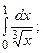
6.38. 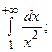 6.39.
6.39. 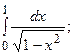
6.40. 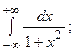 6.41.
6.41. 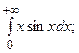
6.42. 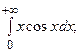 6.43.
6.43. 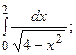
6.44. 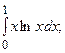 6.45.
6.45. 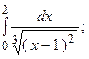
6.46. 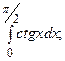 6.47.
6.47. 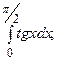
6.48. 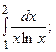 6.49.
6.49. 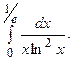
Дата добавления: 2015-07-30; просмотров: 1465;
