Производственных процессов. 1. Ознакомление с основными интервальными оценками рассеяния случайных величин на примерах нормального распределения размеров обработанных деталей.
ЦЕЛИ РАБОТЫ
1. Ознакомление с основными интервальными оценками рассеяния случайных величин на примерах нормального распределения размеров
обработанных деталей.
2. Освоение методов работы со статистическими функциями программы MS Excel, определяющими интервальные оценки рассеяния случайных величин.
3. Сравнение ширины доверительного интервала, полученной как с использованием функции ДОВЕРИТ (удвоенное значение её результата), так и как разницы значений границ доверительного интервала X1, X2 (функция НОРМОБР), рис. 3.1.
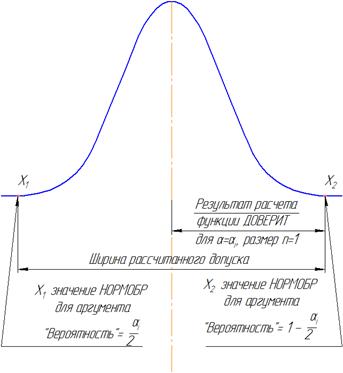
Рис. 3.1. Иллюстрация применяемых способов расчёта
ширины доверительного интервала
4. Анализ зависимости ширины доверительного интервала от величины используемого уровня значимости α; от того рассчитывается ширина доверительного интервала для единичного значения или для выборки и от того, каков объём выборки.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
1. Подготовка к проведению работы.
1.1. Повторение теоретических вопросов по свойствам интегральной функции нормального распределения, точечным и интервальным оценкам рассеяния [6-8].
1.2. Выбор варианта данных для последующего анализа.
1.2.1. Открыть файл MS Excel «лаб. 3 Интервальные оценки рассеяния». Здесь в столбцах (вариантах) представлены результаты контроля размеров деталей 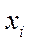 (размер фаски, мм) после их механической обработки (9 деталей).
(размер фаски, мм) после их механической обработки (9 деталей).
1.2.2. С помощью инструмента анализа «ВЫБОРКА» (см. п. 2.1 лабораторной работы № 2) выбрать один из предлагаемых вариантов исходных данных. Для этого ввести во «Входной интервал» строку номеров вариантов, а в число случайных выборок поставить единицу.
1.2.3. Согласовать с преподавателем выбранный вариант.
2. Определение основных точечных оценок.
2.1. Последующие расчеты будут производиться для выбранного варианта, поэтому другие варианты (столбцы данных) можно удалить.
2.2. Определить оценки среднего значения 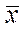 (функция СРЗНАЧ), стандартного отклонения единичного значения
(функция СРЗНАЧ), стандартного отклонения единичного значения 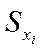 (функция СТАНДОТКЛОН).
(функция СТАНДОТКЛОН).
3. Определение ширины доверительного интервала для нормального распределения случайных величин.
3.1. Открыть функцию ДОВЕРИТ (рис. 3.2).
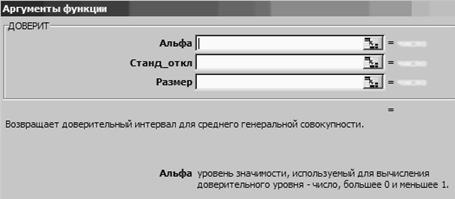
Рис. 3.2. Аргументы функции ДОВЕРИТ
3.2. Подставляя значения стандартного отклонения 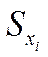 (аргумент «Станд_откл»), различные значения уровня значимости («Альфа» α = 0,05, α = 0,01) и объёма анализируемых данных («размер», n = 1, n = 4 и n = 9), определить ширину доверительного интервала как удвоенного результата расчёта функции ДОВЕРИТ (2*«ДОВЕРИТ»).
(аргумент «Станд_откл»), различные значения уровня значимости («Альфа» α = 0,05, α = 0,01) и объёма анализируемых данных («размер», n = 1, n = 4 и n = 9), определить ширину доверительного интервала как удвоенного результата расчёта функции ДОВЕРИТ (2*«ДОВЕРИТ»).
3.3. Систематизировать полученные результаты в виде таблицы, в которой должны присутствовать: оценки среднего значения 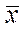 , стандартного отклонения единичного
, стандартного отклонения единичного 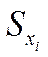 , а также значения ширины доверительного интервала для следующих сочетаний уровня значимости α и объёма данных n:
, а также значения ширины доверительного интервала для следующих сочетаний уровня значимости α и объёма данных n:
– α = 0,05, n = 1
– α = 0,01, n = 1
– α = 0,05, n = 4
– α = 0,01, n = 4
– α = 0,05, n = 9
– α = 0,01, n = 9.
Сделать заключение о влиянии уровня значимости α и объёма данных n на ширину доверительного интервала.
4. Определение границ доверительного интервала для нормального распределения характеристики качества. (Заметим, что, как правило, границы допуска известны, но здесь рассматривается случай, когда необходимо по выборке оценить границы реально достижимого допуска для существующих производственных условий).
4.1. Открыть функцию НОРМОБР (рис. 3.3).
Рис. 3.3. Аргументы функции НОРМОБР
4.2. Подставлять значения стандартного отклонения (аргумент «Стандартное_откл»), среднего значения (аргумент «Среднее») и интегральной функции нормального распределения, выражающей вероятность попадания значения в пределы, ограниченные искомой границей (аргумент «Вероятность») для различных значений уровня значимости α. Аргумент «Вероятность» для определения нижней границы доверительного интервала = α/2, а для определения нижней и верхней границы «Вероятность = 1 – α/2, см. табл. 3.1.
Таблица 3.1
Значения аргумента «Вероятность», необходимые для определения нижней и верхней границы доверительного интервала при разных α
| α | нижняя граница | верхняя граница |
| 0,05 | 0,025 | 0,975 |
| 0,01 | 0,005 | 0,995 |
4.3. Рассчитать ширину доверительного интервала для каждого уровня значимости как разницу между верхней и нижней границами и сравнить со значениями ширины доверительного интервала, полученными с использованием функции ДОВЕРИТ, см. п. 2.2.
4.4. Систематизировать полученные результаты расчётов границ следующим образом:
– нижняя граница допуска для α = 0,05;
– верхняя граница допуска для α = 0,05;
– нижняя граница допуска для α = 0,01;
– верхняя граница допуска для α = 0,01;
– ширина доверительного интервала для α = 0,05;
– ширина доверительного интервала для α = 0,01.
4.5. Сделать заключение о влиянии уровня значимости на положение границ доверительного интервала.
4.6. Сделать заключение о влиянии уровня значимости на ширину доверительного интервала.
4.7. Сравнить значения ширины доверительного интервала, полученной по п. 4.4, как разность между значениями границ этого интервала с соответствующими (полученными для того же уровня значимости α) значениями ширины доверительного интервала, полученными с использованием функции ДОВЕРИТ по п. 3.2 для n=1. Убедиться, что оба метода расчёта приводят к одинаковому результату, как показано на схеме, см. рис. 3.1.
Лабораторная работа № 4.
Дата добавления: 2015-07-30; просмотров: 653;
