Получение и анализ выборочной совокупности случайных величин

ЦЕЛИ РАБОТЫ

1. Освоение методов получения выборки из реальной и воображаемой генеральной совокупности данных о производственном процессе с использованием программы MS Excel.

2. Анализ вариационного ряда выборки случайных величин с получением частотных и интегральных характеристик её рассеяния.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

1. Повторить теоретические вопросы по получению выборочных совокупностей, анализу вариационных рядов, плотности и интегральной функции эмпирических распределений.

2. Получение выборок случайных величин.

2.1. Получение выборки из реальной генеральной совокупности данных. Задача состоит в получении из многотысячных данных о процессе (какой-либо технологической характеристики или параметра качества) ограниченной выборки, удобной для последующего статистического анализа.

2.1.1. Открыть файл «лаб. 2 Генеральная и выборочная совокупность», представляющий собой набор генеральных совокупностей данных усилия резания (P, н), подачи различных инструментов (S, мм), размеров обработанной детали (dH, dh, мм) и т. д. Выделить (нажав на левое верхнее поле), скопировать лист 1 и перенести его содержимое на «Лист для работы». Выбрать для анализа одну генеральную совокупность, расположенную в варианте, соответствующем номеру компьютера (столбец результатов измерения). Остальные генеральные совокупности для удобства дальнейшей работы можно удалить, но необходимо оставить таблицу «Результаты анализа».

2.1.2. Открыть инструмент анализа данных «Выборка» (рис. 2.1).

2.1.3. Ввести во «Входной интервал» выбранную генеральную
совокупность.

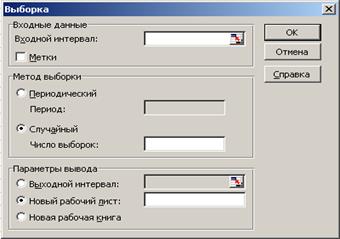
Рис. 2.1. Опции инструмента «Выборка»

2.1.4. В «Параметрах вывода» для того, чтобы получаемые результаты выводились на текущий лист, выбрать «Выходной интервал» и указать ячейку, ниже и правее которой Вам бы хотелось представить результаты анализа (здесь и ниже выбирать ячейки, расположенные правее таблицы результатов анализа, чтобы получаемые результаты не искажали эту таблицу).

2.1.5. Создать механическую (в MS Excel – «периодическую») выборку с периодом 100 данных и случайную выборку объёмом (в MS Excel – «Число выборок») 20 данных и сохранить их для последующего анализа.

2.1.6. С целью преобразования каждой из полученных выборок
(и дальнейших результатов) из столбца в строку (и обратно, если надо) следует воспользоваться опцией «Специальная вставка» и поставить «галочку» в графе «транспонировать», см. примечание к п. 6 лабораторной
работы № 1.

2.1.7. Определить среднее значение и стандартное отклонение для каждой выборки, см. лабораторную работу № 1.

2.2. Получение выборки из воображаемой генеральной совокупности данных. Предполагается, что закон и параметры распределения генеральной совокупности известны.

2.2.1. Открыть инструмент анализа данных «Генерация случайных чисел» (рис. 2.2). Его опция «Распределение» позволяет выбрать непрерывные (равномерное или нормальное)распределения.

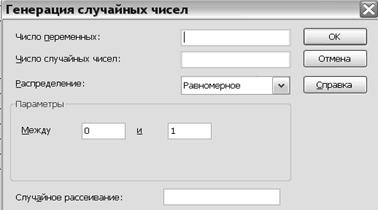
Рис. 2.2. Окно инструмента анализа данных «Генерация случайных

чисел» для равномерного распределения

2.2.2. В опцию «Число переменных» ставим единицу, т. к. в данном случае каждый пользователь рассматривает одну воображаемую генеральную совокупность.

2.2.3. «Число случайных чисел» (объём выборки), как и в предыдущем случае, берём 20 единиц.

2.2.4. Производим генерацию выборок из непрерывных генеральных совокупностей, распределённых по нормальному и равномерному закону. Параметры выборки:

– для равномерного распределения в интервале трёх стандартных отклонений в обе стороны от среднего значения;

– для нормального распределения. (В обоих случаях использовать результаты расчёта «Среднее» и «Стандартное отклонение» п. 2.1.7, полученные для случайной выборки).

2.2.5. Определить среднее значение и стандартное отклонение для каждой выборки, полученной из воображаемой генеральной совокупности данных, см. п. 2.2.4, и объяснить несовпадение их значений, полученных для нормального распределения, с изначально вводимыми значениями.

3. Ранжирование выборки случайных величин (необходимо, в частности, для создания вариационного ряда из произвольно расположенных случайных величин).

3.1. Определение ранга случайных величин, т. е. их величины относительно других значений в выборке в целочисленном (ранговом) и относительном (процентранговом) виде. (Если значения в выборке отсортировать по величине, то ранг числа будет его позицией в этом списке.)

3.1.1. Открыть функцию РАНГ, рис. 2.3.

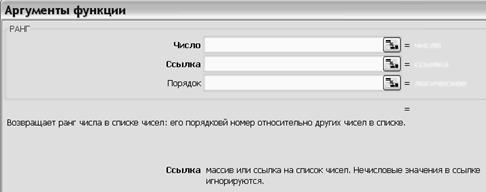
Рис. 2.3. Аргументы функцииРАНГ

3.1.2. Определить ранг первого, второго и третьего чисел в случайной выборке, полученной по п. 2.1.5. Для этого в поле «Число» указываются числа, для которых определяется ранг, а в поле «Ссылка» – сам массив чисел. В поле «Порядок» поставить число 1 (единицу).

Примечания:

1. Поле «Порядок» определяет способ упорядочения. Если в поле «Порядок» стоит 0 (нуль) или оно не заполнено, то программа определяет ранг числа так, как если бы массив был отсортирован в порядке убывания. Если в поле «Порядок» стоит любое ненулевое число, то программа определяет ранг числа так, как если бы массив был отсортирован в порядке возрастания.

2. Функция РАНГ присваивает повторяющимся числам одинаковый ранг. Однако наличие повторяющихся чисел влияет на ранг последующих чисел. Например, если первое и второе числа одинаковы и имеют ранг 10, то следующее число в порядке возрастания, например, третье, будет иметь ранг 12 (и никакое число не будет иметь ранг 11).

3. Функция РАНГ (и функция ПРОЦЕНТРАНГ, см. ниже) может присваивать ранг (или процентранг) не только отдельным (см. п. 3.1.2) но и всем исходным данным. В последнем случае необходима следующая последовательность действий:

– сформировать исходные данные в виде строки или столбца ячеек;

– выделить диапазон ячеек, в который будет введён результат вычислений рангов (например, в виде расположенной рядом строки или столбца);

– вызвать «Мастер функций» и выбрать функцию РАНГ;

– диапазон ячеек с исходными данными поместить в поле «Число» и в поле «Ссылка» аргументов функцииРАНГ, см. рис. 2.3 или в поле «Массив» и в поле «x» аргументов функцииПРОЦЕНТРАНГ, см. ниже рис. 2.4;

– набрать комбинацию клавиш CTRL+SHIFT+ENTER.

3.1.3. Открыть функцию ПРОЦЕНТРАНГ, рис. 2.4 (в десятом офисе эта функция расположена в полном алфавитном перечне функций). В отличие от функции РАНГ здесь оценка производится в относительных величинах: наибольшему значению соответствует 1,0; наименьшему значению соответствует 0, т. е. происходит ранжирование в долевом отношении.

Рис. 2.4. Аргументы функцииПРОЦЕНТРАНГ

3.1.4. Определить ПРОЦЕНТРАНГ первого, второго и третьего чисел в выборке, полученной по п. 2.1.5 и распределённой по нормальному закону. Для этого в поле «x» указываются числа, для которых определяется «процентранг», а в поле «Массив» – сам массив чисел. В поле «Разрядность» указывается количество значащих цифр для определяемого значения. Если этот аргумент отсутствует, то функция ПРОЦЕНТРАНГ выводит число в виде (0,xxx). (Соотношение значений рассчитанных «процентрангов» должны соответствовать соотношению значений рангов этих чисел, см. п. 3.1.2).

3.1.5. Определить РАНГ (в поле «Порядок» ставить единицу) и ПРОЦЕНТРАНГ для всех значений случайной выборки, полученной по п. 2.1.5 (руководствоваться примечанием 3 к п. 3.1.2), сформировав (заполнив) таблицу в «Результатах анализа».

3.2. Определение значения из набора данных, соответствующего заданному относительному положению этого значения.Такую задачу, в определённом отношении обратную задачам функций РАНГ и ПРОЦЕНТРАНГ, решает функция ПЕРСЕНТИЛЬ. Относительное положение изменяется в пределах (персентиль) от нуля до единицы.

3.2.1. Открыть функцию ПЕРСЕНТИЛЬ (рис. 2.5).

Рис. 2.5. Аргументы функции ПЕРСЕНТИЛЬ, где k - значение

персентиля в интервале от 0 до 1 включительно

3.2.2. Использовать функцию ПЕРСЕНТИЛЬ для определения порога приемлемости рассматриваемых данных. В частности, из выбранной генеральной совокупности, см. п. 2.1.1, необходимо устранить крайние по величине результаты, имеющие значение персентиля больше 0,95 и меньше 0,05. Для этого следует в поле «к» (см. рис. 2.5) поставить 0,95 (95-й персентиль) и определять максимально допустимое значение результатов, а затем – поставить 0,05 (5-й персентиль), определяя минимально допустимое значение результатов.

3.3. Использование инструмента анализа «Ранг и персентиль» для определения рангов и персентилей всего массива данных.

3.3.1. Открыть инструмент анализа «Ранг и персентиль» (рис. 2.6), ввести данные во «Входной интервал» (выборку, полученную для нормального распределения из воображаемой генеральной совокупности по п. 2.2.4), и в зависимости от того, как они расположены, поставить «по столбцам» или «по строкам».

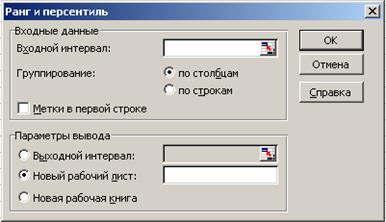
Рис. 2.6. Инструмент анализа данных «Ранг и персентиль»

3.3.2. Расположить полученные данные на новом рабочем листе и убедиться, что этот инструмент в отличие от соответствующих функций не просто определяет ранги и персентили, а сортирует их в порядке уменьшения значения.

4. Получение частотных и интегральных характеристик рассеяния генеральной совокупности (выбранной Вами по п. 2.1.1).

4.1. Построение интервального вариационного ряда.

4.1.1. В таблице MS Excel построить массив границ интервалов (который в аргументах функции «Частота» на рис. 2.7 представлен как «Массив интервалов», а в ряде версий MS Excel – как «Двоичный массив»). Для правильного построения массива границ интервалов нужно:

а) выбрать количество интервалов m одним из двух способов:

– просто задать m = 10-12;

– рассчитать m в зависимости от объёма массива данных n по формуле, например, ;

б) оценить длину интервала: L = (D_max – D_min)/m;

в) округлить минимальное значение (D_min) до трёх знаков, поместив результат в отдельную ячейку, что и будет нижней границей интервалов;

г) правой кнопкой мыши «потянуть» ячейку за правый нижний угол вниз на m ячеек, нажать на опцию «Прогрессия» в открывшемся контекстном меню и выбрать «Шаг», равный значению длины интервала L.

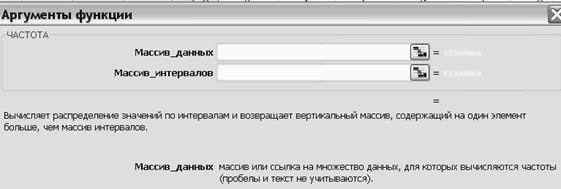
Рис. 2.7. Аргументы функции ЧАСТОТА

4.1.2. Выделить массив ячеек, куда в результате будут введены значения частот (на единицу больше числа заданных границ интервалов за счёт того, что первый и последний интервалы ограничены лишь с одной стороны).

4.1.3. Открыть функцию ЧАСТОТА (см. рис. 2.7).

4.1.4. Ввести в окна аргументов массив Ваших данных, см. п. 2.1.1, и массив границ интервалов (аргумент «Массив_интервалов»). При этом значения частот уже появляются в окне.

4.1.5. Нажать одновременно комбинацию клавиш CTRL+SHIFT+ENTER, получив распределение частот «попаданий» значений из Вашей генеральной совокупности в выделенный по п. 4.1.2. массив интервалов, разделённых границами, полученными по п. 4.1.1.

4.1.6. Сформировать интервальный статистический ряд, состоящий из двух строк:

– строки границ интервалов, в которой первый и последний интервалы ограничены с одной стороны, а со второй – соответственно –∞ и +∞;

– строки значения частот, попавших в заданные интервалы.

(Для транспонирования столбцов в строки и обратно использовать опцию «Специальная вставка», см. п. 6 лабораторной работы № 1).

4.2. Построение диаграммы распределения частот, то есть графика функции плотности дискретного распределения (гистограммы), и диаграммы накопленных частот, иначе – графика интегральной функции дискретного распределения.

4.2.1. Открыть инструмент анализа «Гистограмма» (см. рис. 2.8), который по решаемым задачам близок к функции «ЧАСТОТА», но имеет значительно более широкие возможности. В нём поле «Входной интервал» соответствует полю «Массив данных» в функции «ЧАСТОТА». Поле «Интервал карманов» соответствует полю «Массив интервалов» в функции
«ЧАСТОТА».

4.2.2. Ввести массив Ваших данных, см. п. 2.1.1, в поле «Входной интервал». При заполнении поля «Интервал карманов» (не обязательно для заполнения, т. к. программа сама создаёт набор отрезков, равномерно распределённых между минимальным и максимальным значениями данных) значения границ интервалов должны быть введены в возрастающем порядке.

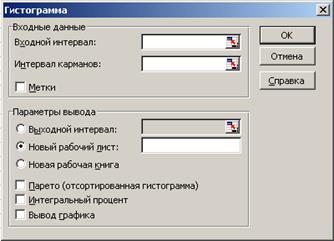
Рис. 2.8. Инструмент анализа данных «Гистограмма»

4.2.3. Поставить «галочки» в поля «Вывод графика», «Интегральный процент» и нажать «ОК». Программа MS Excel вычисляет число попаданий данных между текущим началом интервала и соседним бóльшим по порядку, причём включаются данные на нижней границе и не включаются данные на верхней границе интервала, а сами интервалы располагаются в возрастающем порядке. По этим данным строится собственно гистограмма (синего цвета) и диаграмма накопленных частот (розового цвета).

4.2.4. Поставить дополнительную «галочку» в поле «Парето (отсортированная диаграмма)», чтобы интервалы располагались не в возрастающем порядке, как обычно, а в порядке убывания частоты. Проследить, как в этом случае изменится вид гистограммы и диаграммы накопленных
частот.

4.2.5. Построить гистограмму в рамках графических опций программы («Мастер диаграмм» тип «Гистограмма»), сравнить с графиками, полученными по п. 4.2.3, и сделать выводы о преимуществах гистограммы, построенной в рамках статистического анализа.

Лабораторная работа № 3.