Характеристики качества (размера) в пределы поля допуска

Примечание. Задача решается путём сравнения вероятности попадания размера в пределы поля допуска, полученной по п. 3 с вероятностями, полученными аналогично для случаев, когда точность обработки уменьшена (соответственно дисперсия увеличена в 2 раза S_увел. = 2* 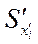) и точность увеличена (соответственно дисперсия уменьшена в 2 раза
S_{уменьш.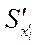} = /2).

4.1. Определить долю годной продукции при той же настройке (посередине поля допуска), см. п. 3.6, но при обработке со вдвое большей точностью, чем ранее.

4.2. Определить долю годной продукции при той же настройке, см. п. 3.6, но при обработке со вдвое меньшей точностью, чем ранее.

4.3. Определить, на сколько % и во сколько раз для Вашего распределения увеличивается суммарный % годной продукции с увеличением точности обработки в четыре раза.

4.4. Определить, на сколько % и во сколько раз для Вашего распределения увеличивается суммарный % годной продукции с увеличением точности обработки от минимальной (максимальное S_увел. = 2* ) в два раза и ещё раз в два раза.

4.5. Объяснить, пользуясь схемой, представленной на рис. 4.4, почему, по Вашему мнению, кратное повышение точности не приводит к пропорциональному увеличению вероятности получения годной продукции?

5. Попытка упрощённого определения оптимального положения центра настройки

Примечание. В случае, когда выход характеристики качества в различные стороны за пределы поля допуска различается по своим последствиям (образуется в одном случае исправимый, а в другом – неисправимый брак) задача выбора оптимального положения центра настройки значительно усложняется. Для точного решения этой задачи требовалось бы определение экстремума (максимума) функции экономии (Э), складывающейся из нескольких компонентов, зависящих от величины смещения относительно середины допуска (с): экономии от реализации годной продукции (РГП), потерь на исправимый (ПИ) и на неисправимый (ПН) брак:
Э = РГП(с) – ПИ(с) – ПН(с) и использование итерационного процесса (способа постоянного приближения).

5.1. Задаться предположением, что экономические потери, возникающие при получении неисправимого брака, в 4 раза превышают потери, образующиеся при получении исправимого брака.

5.2. Определить из результата, полученного по п. 3.6, долю продукции, приходящуюся на исправимый и неисправимый брак вместе (Σ_α), при том, что всё её количество взято за единицу.

5.3. Разделить полученную долю бракованной продукции на доли, приходящиеся на исправимый (α_исп) и неисправимый (α_неисп) брак отдельно. Задаваясь предположением, что доля исправимого брака должна быть соответственно п. 4.1 в 4 раза больше, чем доля неисправимого брака (α_исп/α_неисп = 4, хотя это не вполне корректно), рассчитать доли, приходящиеся на каждый вид брака: α_исп и α_неисп.

5.4. Для расчёта вновь полученных границ допуска 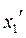(минимальное граничное значение) и 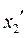(максимальное граничное значение), соответствующих полученным по п. 4.3 α_исп и α_неисп использовать функцию НОРМОБР. При этом, предполагая, что Вы обрабатываете вал для расчёта 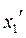в качестве аргумента «Вероятность» следует брать α_неисп, а для расчёта 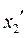– значение 1-α_исп. (Сравните с п. 4.2 лабораторной работы № 3).

5.5. Определить середину ( 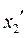+ 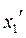)/2 и ширину ( 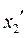– 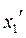) вновь полученного поля допуска. Сравнить, как ширина допуска ( 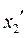– 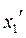) изменилась по сравнению с её предыдущим значением (x₂–x₁) и попытаться объяснить (подумать!) такое изменение.