Перехід до створення математичної моделі

· Параметризація моделі – визначають параметри, якими можна описати систему.

· Встановлення залежностей між параметрами всередині системи і навколишнім середовищем.

· Виявлення характерних особливостей цих залежностей і згуртування їх в задачі.

Моделі розв’язують два типи задач:

1. Задачі прямого рахунку – допомагають швидше розв’язати задачу і прийняти рішення.

2. Оптимізаційні, багатоваріантні задачі, які зводяться до знаходження найкращого вирішення і підтримки цього найкращого вирішення в управлінні.

Будь-яка стратегія управління базується на певному розумінні того, як фізичний процес реагує на вхідний сигнал.

На відміну від науки, де метою моделювання є глибоке вникнення в суть системи, модель в інженерному розумінні вважається адекватною, якщо всі відповідні процеси управління працюють в передбачуваному режимі, тобто є стійкий вихід з малими відхиленнями від заданого значення.

Розрізняють такі типи моделей:

1. Безперервний в часі (аналоговий) опис.

Система описується лінійними чи нелінійними диференційними рівняннями балансу маси, енергії чи сил.

В багатьох випадках нелінійні рівняння можна лінеаризувати і тим самим спростити роботу з ними.

2. Дискретний в часі опис.

Фізичні властивості описуються лінійними чи нелінійними різницевими рівняннями. Такий підхід означає, що інформація про систему доступна тільки в певні дискретні моменти часу. Цей тип опису в дійсності майже неминучий при цифровому керуванні, оскільки комп’ютери, які базуються на найбільш поширеній архітектурі фон Неймана, виконують інструкції послідовно.

3. Моделі систем, що грунтуються на дискретних подіях чи послідовності подій.

При такому описі вхідні та вихідні величини системи дискретні в часі і є бінарними сигналами типу: “включено-виключено”. Багато систем управління послідовністю можна описати як систему черг і моделювати марківськими ланками чи марківськими процесами.

4. Моделі систем з невизначеністю.

Як на самі системи управління, так і на вимірювання часто впливають небажані шуми і збурення. В одних випадках збурення і неповні знання про фізичний процес можна інтерпретувати статистично. В інших – фактори невизначеності замість кількісних характеристик можна описувати лінгвістичними і логічними виразами типу “якщо-то інакше” (експертні системи).

Ще один спосіб опису невизначеності систем – нечітка алгебра (fuzzy).

Не зовсім вірним є твердження, що процес можна вичерпно описати тільки одною моделлю. В дійсності правильно навпаки.

Найбільш правильною є найпростіша модель з можливих моделей, але така, що забезпечує управління об’єктом, котре задовольняє заданому критерію якості.

1.9. Спостережність і керованість

Існують два основні способи розробки моделей:

· на основі фізичних принципів

· на основі експериментальних даних (результатів вимірювання)

Якщо дані вимірювань використовуються в контексті знань про систему управління, то можна розрахувати значення, які не вдається виміряти. Процедура розрахунку чи оцінки значень змінних є наслідком однієї з основних характеристик системи, яка називається спостережністю.

Спостережність – це оцінка того, чи дає наявний набір вимірювання адекватну інформацію про систему.

Керованість показує, чи достатньо параметрів системи, на котру можуть впливати виконуючі механізми для управління процесом необхідним чином.

Система називається керованою, якщо можна підібрати такі значення U, щоб система досягла заданого значення Х.

Тільки тоді, коли система керована, її полюси (власні числа) можна вільно переміщувати за допомогою зворотнього зв’язку.

Якщо процес некерований – це означає, що частини системи фізично від’єднані від управляючих (керуючих) сигналів U.

Змінні стану системи:

...

...

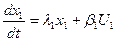
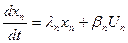
В матричній формі:

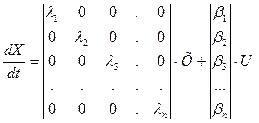
Управляючі сигнали впливають на кожну змінну окремо. В керованій системі всі елементи матриці B ненульові. В іншому випадку змінні стану, що відповідають нульовим елементам матриці В, не можуть регулюватися сигналом управління. Значення таких змінних будуть визначатися тільки властивостями системи.

Треба добре розуміти фізичний процес інженеру. Наприклад, часто буває так, що параметри погано керовані, тобто значення b_i малі. Система формально керована, а реальний регулятор для практичного використання створити неможливо.

Якщо ж система працювала задовільно, то при автоматизації (комп’ютеризації) робота системи покращиться. Якщо система працювала незадовільно, то після автоматизації вона працювати не буде.

1.10. Структури організаційних систем

Структури реальних систем надзвичайно різноманітні, але всю множину відомих ієрархій можна розділити на 3 основні типи, залежно від видів зв’язків між елементами:

· лінійна;

· функціональна (лінійно-функціональна);

· матрична.

1.10.1. Лінійні структури

При лінійній структурі кожний елемент має тільки одного начальника, зв’язки лінійні. Така структура передбачає чітке розділення повноважень і обов’язків елемента.

Недоліки: складність координації між елементами, оскільки на першому ступені вищий елемент повинен бути компетентним у всіх питаннях роботи нижчого. Лінійна структура, зображена на рис. 1.22, використовується в системах з порівняно простими функціями елементів.

1.10.2. Функціональні структури

В функціональній структурі передбачена спеціалізація.

Недоліки: невирішена проблема координації, оскільки кожен нижчий елемент отримує команди від кількох керівників і тому не завжди можна визначити порядок їх виконання. В міру ускладнення управління виникають нові функціональні підслужби, і виконавці отримують ще більшу кількість керівників, що призводить до дезорганізації.

1.10.3. Матричні структури

Матричні структури зображено на 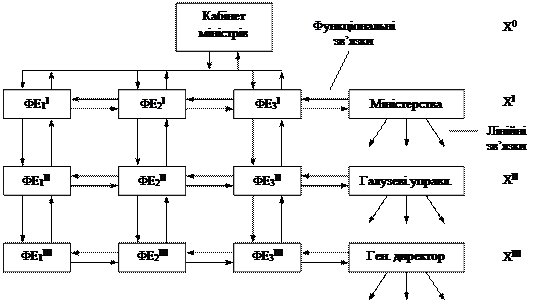рис. 1.23:

Кожний функціональний елемент знаходиться в подвійному підпорядкуванні. Матрична структура передбачає наявність підрозділів і досить широко застосовується на підприємствах і в наукових установах.

1.11. Структури інформаційних систем

Структури інформаційних схем – це структури, по яким передається інформація.

1.

Переваги: простота

Недоліки: мала швидкодія, велика можливість помилкової інформації.

2. Паралельні структури

3. Кільцеві структури

4. Багатозв’язна інформаційна структура

Кожен елемент зв’язаний з кожним. Максимальна швидкість передачі інформації.

5.

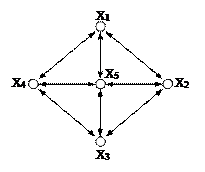Структура типу “колесо”

Характеризується великою швидкістю передачі інформації.

 

1.12. Задачі аналізу і синтезу системи

 

При розв’язку технічних (динамічних) систем може бути поставлена задача аналізу або синтезу.

Аналіз системи передбачає визначення зв’язку між входом і виходом (наприклад, у виді алгебраїчного чи диференціального рівняння), а також знаходження опосередкованих показників якості системи (швидкодії, точночті).

При розв’язуванні задач аналізу відома структура всієї системи і параметри об’єкта управління. Завдання розробки системи управління зводиться до визначення параметрів управляючого органу або регулятора, який би забезпечував задані статичні і динамічні показники системи управління.

Задача синтезу полягає в визначенні структури системи, її параметрів, за заданою метою управління (цільовою функцією). Як правило, синтез систем зводиться до синтезу управляючого органу, тому що структура і параметри ОУ відомі.

1.13. Оптимальне управління

 

Оптимальним називається управління, яке здійснюється найкращим чином за певним показником.

Системи, що реалізують оптимальне управління називаються оптимальними.

Організація оптимального управління грунтується на виявленні і реалізаціі граничних можливостей системи. Одним із найважливіших кроків є формулювання критерію оптимальності, під яким розуміється основний показник, що визначає задачу оптимізації. У якості критерію оптимізації виступають різні технічні чи техніко-економічні показники, які виражають технічну чи економічну вигоду (втрати).

Узагальнений критерій якості роботи лінійних динамічних систем можна зобразити у вигляді функціоналу якості чи ефективності:

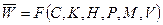, де

С – вартість

К – якість функціонування

Н – надійність

Р – споживана потужність

М – маса

V – об’єм чи габарити

Оптимізувати функціонал 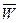по всім параметрам одночасно неможливо.

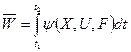
U=(u₁,u₂,…,u_n)

X=(x₁,x₂,…,x_n)

F=(f₁,f₂,…,f_n)