Поняття системи
Приклад декомпозиції системи зображено на рис. 1.17:
  |
Рис. 1.17.
Поняття “системи” можна характеризувати наступним чином:
1. Поняття “системи” дозволяє простіше інтерпретувати призначення складної структури, що складається із взаємодіючих одна з однією частин.
2. Описуючи систему, її можна по-різному розбити на складові частини. Кожна з частин, в свою чергу, може бути розбита на більш дрібні складові. Важливо правильно вибрати рівень деталізації.
3. Як правило, немає необхідності знати внутрішні механізми елементу для того, щоб передбачити поведінку системи в цілому, достатньо знати перетворення “вхід” – “вихід” (принцип “чорної скриньки”).
4. Метою системи є отримати результат якісно чи кількісно більший від простої суми результатів окремих її компонентів. Об’єднання в систему додає “дещо більше”, що і пояснює її призначення. Це “дещо більше” визначається не наявністю тих чи інших компонентів системи, а, скоріш за все, їх взаємодією (принцип синергізму). Приклад – лікарські набори трав, їх вплив на організм людини.
1.6. Структуризація системи
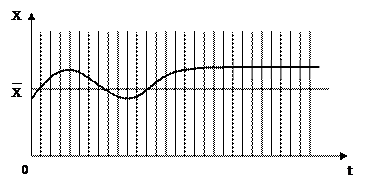 |
Питання визначення внутрішньої структури та питання границь системи є важливим питанням при аналізі чи синтезі систем. Тут важливо визначити сильні і слабкі зв’язки. На рис. 1.18 зображене графічне зображення двох процесів Х і Y.
 |
Рис. 1.18.
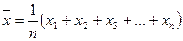
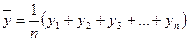
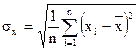 - відхилення по X
- відхилення по X
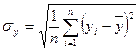 - відхилення по Y
- відхилення по Y
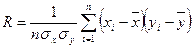 - взаємокореляційна функція
- взаємокореляційна функція
R може набувати значення від 0 до 1.
Якщо R=0 – система немає зв’язків – система слабко структурована.
Якщо R=1 – система детермінована або сильно структурована.
Якщо RÎ(0÷0,5] – система з слабкими зв’язками.
Якщо RÎ[0,5÷1) – система з сильними зв’язками.
1.7. Класифікація систем за складністю
1. Проста система – кількість елементів =10...103
2. Складна система – кількість елементів =104...107
3. Ультраскладна система – кількість елементів =108...1030
4. Суперскладна система – кількість елементів =1031...10200
Якщо систему можна описати тільки одним математичним апаратом, то вона буде відноситися до простих. Чим більше математичних апаратів необхідно застосувати для опису – тим складніша система.
Проста система – система, яка не має розгалуженої структури.
Складна система – система з розгалуженою структурою і значною кількістю взаємозв’язаних елементів, які, в свою чергу, є простими системами.
Велика система – складна система, яка має такі ознаки:
1. Наявність виділених складових (підсистем), які мають своє призначення, що підпорядковане загальному призначенню.
2. Наявність великої кількості різноманітних зв’язків між підсистемами і всередині кожної з підсистем.
3. Наявність зовнішніх зв’язків з іншими підсистемами, системами.
4. Наявність у системі елементів самоорганізації.
5. Участь у функціонуванні системи людей, машин та природнього середовища.
1.8. Моделювання в управлінні
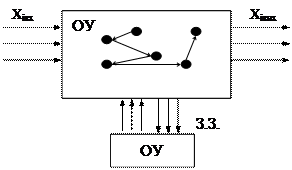 Моделювання в управлінні зображене на рис. 1.19:
Моделювання в управлінні зображене на рис. 1.19:
Рис. 1.19.
Закон кібернетики: Складність управляючого органу tу.о. повинна бути не меншою, ніж складність об’єкту управління tо.у. .
Для оптимального управління системою на кожне відхилення (стан) повинна бути відповіднауправляюча дія (реакція).
t=nm
1.8.1. Модель
Прямо управляти складними системами за рахунок великої складності дуже важко, тому здійснюють управління через моделі tмоделі<tсистеми .
Модель – спрощене представлення системи. Модель створюється для того, щоб проаналізувати систему. Модель полегшує оцінку змісту системи і прогнозування її розвитку, тому ОУ представляють у вигляді моделей. Модель може бути занадто спрощена, оптимальна або переускладнена. Степінь адекватності моделі управління здійснюється шляхом експериментів.
1.8.2. Види моделей
1. Статична модель – це модель, яка зв’язує вихідну величину з вхідною незалежно від часу. Статична модель зображена на рис. 1.20:
Статична модель Динамічна модель
Вольт-амперна характеристика діода

Рис. 1.20. Рис. 1.21.
Динамічна модель, зображена на рис. 1.21, пов’язує зміну вихідної величини в часі відносно зміни вхідної величини в часі.
2. Неформалізовані моделі можуть бути здійснені в довільній формі. Вони створюються за допомогою тестування.
3. Математичні моделі – це моделі, в яких чітко визначена математична залежність типу: y=f(x).
Дата добавления: 2015-07-24; просмотров: 758;
