Оптимальність за споживаною потужністю
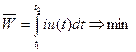
В залежності від реалізованого критерію системи розрізняють на:
Ø системи, оптимальні за швидкодією;
Ø системи, оптимальні за точністю;
Ø системи, оптимальні за інваріантністю від збурень;
Ø системи, оптимальні за споживаною потужністю.
Список літератури до розділу 1:
1. Густав Олсон, Джангуидо Пиани Цифровые системы автоматизации и управления. – СПб.: Невский Диалект, 2001. – 557с.
2. Куропаткин П.В. Оптимальные и адаптивные системы. – М.: Высшая школа, 1980. – 287с.
3. Петренко А.И. Основы автоматизации проектирования. – К.: Техника, 1982. – 293с.
Розділ 2. Лінійні динамічні системи
2.1. Математичне моделювання лінійних динамічних систем (ЛДС)
Лінійними називаються системи, котрі в статиці і в динаміці описуються лінійними рівняннями.
Для ЛДС притаманний принцип суперпозиції, який полягає в тому, що реакція системи на сукупність сил та збурень визначається сумою реакцій на кожну силу чи збурення, що прикладаються до системи.
Реальні системи, особливо складні, є суттєво нелінійними. До лінійного опису можна звести незначний клас систем, але і в цьому випадку властивості реальних систем тільки наближено виражаються лінійними моделями.

Рис. 2.1. Рис. 2.2
Незважаючи на обмеження лінійних моделей, їх роль у ТОУ дуже велика. Це пояснюється тим, що припущення про лінійність системи в ряді випадків не призводить до недопустимих помилок, а з іншого боку суттєво спрощує дослідження системи. Ілюстрація способів лінеаризації приведена на рис. 2.1 і рис. 2.2.
Методи дослідження реальних нелінійних систем (НС) в значній мірі базуються на методах дослідження ЛДС, наприклад – метод гармонічного балансу.
Лінійна теорія управління дозволяє вивчати лінійні моделі реальних процесів і об’єктів, а не самі процеси і об’єкти.
Будь-яку ЛДС можна представити у вигляді сукупності наступних типових структурних ланок:
Ø аперіодичної
Ø коливної
Ø інтегруючої
Ø диференціюючої
Ø консервативної
Ø ланки з запізненням
Кожна з типових ланок достатньо повно характеризується формою диференційних рівнянь, видом передатної і перехідної функції.
Типовою ланкою називається ланка, яка описується інтегро-диференційними рівняннями не вище другого порядку. На рис. 2.3 зображено декомпозицію системи 6-го порядку на типові ланки.
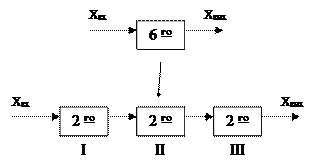
Рис. 2.3.
ЛДС в загальному випадку описується диференційним рівнянням n-го порядку:
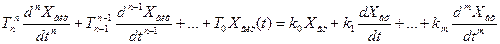 /1/ -
/1/ -
рівняння руху системи
Вихідна дія Þ вхідна дія
Т0...Тn , k0…km - параметри налаштування системи
2.1.1. Приклади створення математичного опису моделі
Приклад 1.
Складання рівняння руху електричної схеми, зображеної на рис. 2.4.
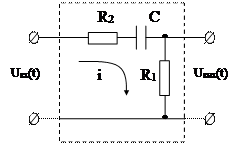 Uвх(t) – вхідна дія
Uвх(t) – вхідна дія
Uвих(t) – вихідна дія
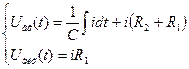
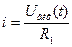
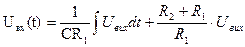
Рис. 2.4.
Диференціюємо і переміщаємо у рівнянні вихідні змінні вліво, вхідні – вправо.
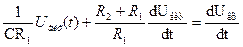
Коефіцієнт при нульовій похідній в лівій частині рівняння має бути рівним 1. Отже, домножуємо на СR1.

Позначимо 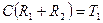 ;
; 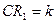 . Тоді
. Тоді
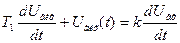 - рівняння руху системи
- рівняння руху системи
або 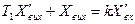
Приклад 2.
Складання рівняння руху електричної схеми, зображеної на рис. 2.5, і знаходження передатної функції (W(p)).
Характерним для ОП є високий коефіцієнт підсилення по напрузі k=104…106 , отже U0»0.
|
|
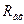 - високе приймемо
- високе приймемо 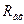 = ∞
= ∞
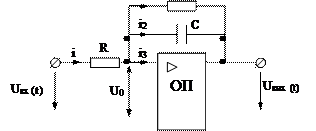 |
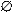



Рис. 2.5.
Складаємо рівняння руху системи:
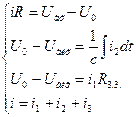 /1/-/4/,
/1/-/4/, 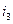 =0, бо
=0, бо 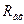 операційного підсилювача →∞
операційного підсилювача →∞
З рівняння /1/: 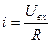 , бо
, бо 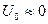
З рівняння /2/: 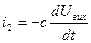 , бо
, бо 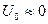
З рівняння /3/: 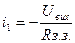
З рівняння /4/: 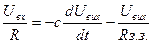 /*Rз.з.
/*Rз.з.
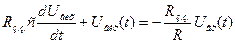 – рівняння руху системи (5)
– рівняння руху системи (5)
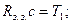
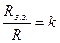 - коефіцієнт підсилення
- коефіцієнт підсилення
Знак “–” в рівнянні (5) означає, що вихідна напруга зсунута за фазою -π (180°), як зображено на рис. 2.6.
 |
Рис. 2.6.
або
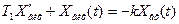
Зображення рівняння руху системи в операторній формі:
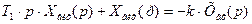
Передатна функція:
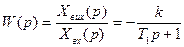
Приклад 3.
Складання рівняння руху електро-механічної системи і знаходження передатної функції, поданої на рис. 2.7.
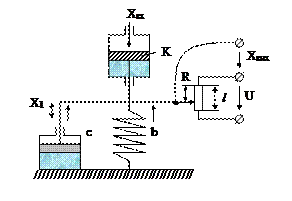 |
Рис. 2.7.
Тиск повітря на клапан К є вхідною величиною. Вихідною величиною є напруга, яка знімається з потенціометра R. При зміні тиску змінюється сила, яка прикладена до штоку поршня, внаслідок чого переміщується зв’язаний з ним повзунець потенціометра R. Переміщення X1 залежить від сил, які діють на поршень.
| Діючі сили: | |
| Сила тиску на поршень (пропорційна тиску Хвх) | aХвх |
| Сила протидії пружини (пропорційна деформації Х1) | bX1 |
Сила в’язкого тертя
(пропорційна швидкості 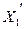 переміщення) переміщення)
| 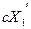
|
| Сила інерції | 
|
Складаємо балансове рівняння:
aХвх-bX1- 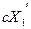 =
= 
m – маса поршня і зв’язаних з ним деталей
 +
+ 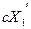 +bX1=aХвх /1/
+bX1=aХвх /1/
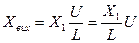 /2/
/2/
Підставляємо в /1/ співвідношення /2/ і домножуємо ліву і праву частину на коефіцієнт так, щоб при 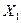 була 1.
була 1.
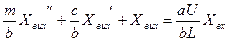
Введемо позначення:
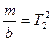 ;
; 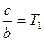 ;
; 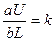 ;
;
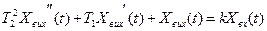 /3/ – рівняння руху системи
/3/ – рівняння руху системи
Зображення рівняння руху системи в операторній формі:
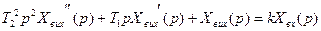
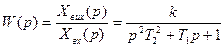
В деяких випадках зручніше визначити передатну функцію ланки (системи), а потім з неї записати рівняння руху системи (приклад 4,5).
Приклад 4.
Знаходження W(p) мостової електричної схеми, зображеної на рис. 2.8.
Вхідна дія – напруга на вході 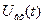
Вихідна дія – напруга на другій діагоналі 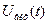
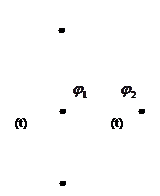

Рис. 2.8.
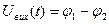
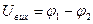
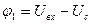
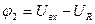
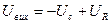
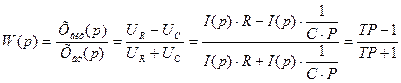
де T=RC – постійна часу
Приклад 5
Знаходження передатної функції електричної схеми, зображеної на рис. 2.9.

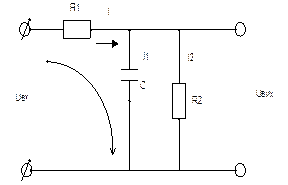
Рис. 2.9.
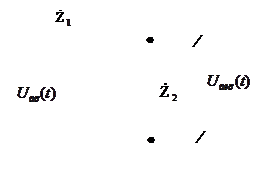
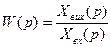
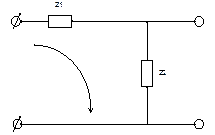
Ż  =
= 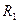
|
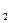 =
= 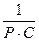 ||R
||R 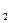 =
= 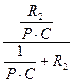 =
= 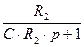
Тоді
|
|
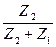 =
= 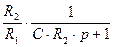 =
= 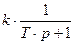
де k= 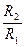 , T=
, T= 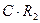
2.2. Передатна функція
Передатною функцією називаєтьсявідношення перетвореної за Лапласом вихідної дії до перетвореної за Лапласом вхідної дії при нульових умовах і відсутності збурень.
Нульові початкові умови означають не тільки рівність f(t)=0 при t=0, але й нульові умови у всіх похідних до (n-1) включно, де n – порядок системи.
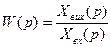
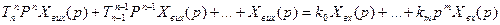 - зображення рівняння руху системи в Лапласівській формі,
- зображення рівняння руху системи в Лапласівській формі,
де 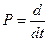
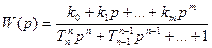
З іншого боку р=jw, де w=2pf – кутова частота, а 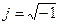 .
.
2.3. Правила спрощення структурних схем
Часто буває так, що реальна система (чи модель системи) зображається сукупністю зв’язаних між собою передатних функцій, які утворюють складну структурну схему.
При задачі аналізу виникає потреба знаходження результуючої передатної функції, тобто спрощення структурної схеми.
Приклад 1.
Спрощення структурної схеми, зображеної на рис. 2.10, до виду, зображеного на рис. 2.11.
 |
Рис. 2.10. Рис. 2.11
1.Послідовне з’єднання:
 |
2.
 |
Паралельне з’єднання:
3.Зворотній зв’язок:
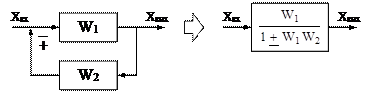 |
4.  Переміщення вузла проти проходження сигналу:
Переміщення вузла проти проходження сигналу:
5.
 |
Переміщення вузла за проходженням сигналу:
Якщо вузол переноситься проти напрямку проходження сигналу, то у вітку, що переноситься, необхідно включити всі елементи з передатними функціями, які зустрічаються між старим і новим вузлом.
Якщо вузол переноситься за напрямком проходження сигналу, то у вітку, що переноситься, необхідно включити всі елементи з оберненими передатними функціями, які зустрічаються між старим і новим вузлом.
6.
 |
Переміщення точки сумування за проходженням сигналу:
7.Переміщення точки сумування проти проходження сигналу:
 |
Якщо точка сумувань переноситься за напрямком проходження сигналу, то у вітку, що переноситься, необхідно включити передатні функції всіх елементів, які зустрічаються на шляху між старою і новою точками сумування.
Якщо точка сумувань переноситься проти напрямку проходження сигналу, то у вітку, що переноситься, необхідно включити елементи з оберненими передатними функціями всіх елементів, які зустрічаються на шляху між старою і новою точками сумування.
Результуюча передатна функція структурної схеми, зображеної на рис. 2.10, використовуючи правила 1-3, буде мати вид
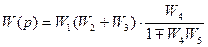
2.4. Частотні характеристики
Розрізняють 4 типи частотних характеристик:
1.АФЧХ – амплітудо-фазо-частотна характеристика.
2.АЧХ - амплітудо-частотна характеристика.
3.ФЧХ - фазо-частотна характеристика.
4.ЛАФЧХ – логарифмічна амплітудо-фазо-частотна характеристика.
Оскільки більшість задач можна розв’язати в частотній області, наприклад, оцінити стійкість системи, визначити запас стійкості, розрахувати коректуючі елементи і т. ін., то повернення в часову область (зворотнє перетворення Лапласа) може не здійснюватись.
Амплітудо-фазо-частотна характеристика – це геометричне місце кінців вектора передатної функції при зміні частоти від 0 до +¥.
2.4.1. Шляхи побудови АФЧХ
Розрізняють 2 шляхи побудови АФЧХ:
1.Експериментальний шлях побудови АФЧХ
а). Змінюючи частоту 0<w<¥ визначаємо модуль коефіцієнта передачі
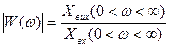
Хвих, Хвх – амплітудні значення дій.
б). Вимірюємо фазову характеристику j(w) при зміні частоти 0<w<¥.
в). АФЧХ будується на комплексній площині. На промені кута φ відкладаємо відповідне значення модуля |W(ω)|.
W(w)=Re(w)+Im(w)=a(w)+jb(w) – рівняння руху системи 3-го порядку.
Графік побудови АФЧХ експериментальним шляхом зображено на рис. 2.12.
 |
Рис. 2.12.
2.Теоретичний шлях побудови АФЧХ
а). Необхідно мати рівняння руху системи
C(p)Xвих(p)=B(p)Xвх(p)
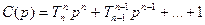
B(p)=(k0+k1p+…+kmpm)
б). Знаходимо передатну функцію
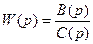
в). Замінюючи р=jw, знаходимо:
W(w)=a(w)+jb(w)
г). Змінюючи w від 0 до ¥ на комплексній площині будуємо графік АФЧХ (W(w))
Графік побудови АФЧХ теоретичним шляхом зображений на рис. 2.13.
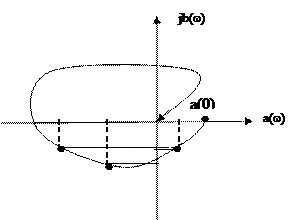 |
Рис. 2.13.
Приклад:
Побудова АФЧХ теоретичним шляхом для системи 2-го порядку.
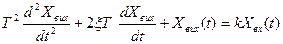 - рівняння руху системи
- рівняння руху системи
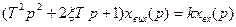 - лапласівське зображення рівняння руху системи
- лапласівське зображення рівняння руху системи
x - коефіцієнт загасання
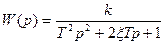
Замість р підставляємо jw:
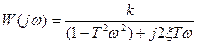
Домножуємо чисельник і знаменник на спряжений вираз: 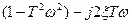 , тоді
, тоді
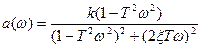
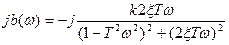
АФЧХ будується, підставляючи w від 0 до ¥ в вирази дійсної а(ω) і уявної b(ω).
Кількість квадрантів, які займає годограф передатної функції, рівна порядку системи (рис. 2.14).
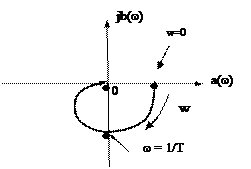
Рис. 2.14.
2.5. Амплітудо-частотна характеристика (АЧХ)
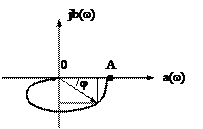
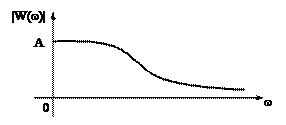 |
Амплітудо-частотною характеристикою називається залежність модуля передатної функції від частоти, при зміні частоти від 0 до ¥. АЧХ зображена на рис. 2.15 як модуль від АФЧХ рис. 2.16.
Рис. 2.15. Рис. 2.16.
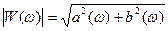
2.6. Фазо-частотна характеристика (ФЧХ)
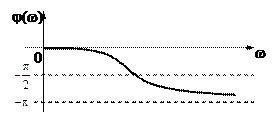 |
Фазо-частотною характеристикою називається залежність фазового зсуву між вихідною та вхідною дією при гармонічному вхідному сигналі. Приклад ФЧХзображено на рис. 2.17:
Рис. 2.17.

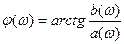
Будувати АЧХ та ФЧХ по осі абсцис бажано в однаковому масштабі.
2.7. Особливості АФЧХ. Зв’язок між АФЧХ і перехідною функцією
1.Границя, до якої прямує функція при t®¥ рівна значенню АФЧХ при w=0.
2.Значення перехідної функції при t=0 рівня граничному значенню АФЧХ при w®¥.
3.Якщо перехідна функція при t=0 має певну швидкість зміни 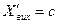 , то АФЧХ при w®¥ прямує до
, то АФЧХ при w®¥ прямує до 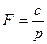 , (р=jw), як до границі, отже наближається до початку координат, рухаючись вертикально знизу вверх.
, (р=jw), як до границі, отже наближається до початку координат, рухаючись вертикально знизу вверх.
4.Якщо перехідна функція починається при t=0 з горизонтальної дотичної і має певне прискорення 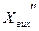 =d, то АФЧХ при w®¥ прямує до
=d, то АФЧХ при w®¥ прямує до 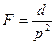 як до границі і наближається до початку координат, рухаючись горизонтально зліва направо.
як до границі і наближається до початку координат, рухаючись горизонтально зліва направо.
2.8. АФЧХ при від’ємних частотах. Від’ємна АФЧХ. Обернена АФЧХ
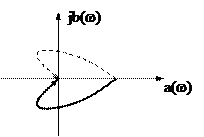 |
1. W(-w)
АФЧХ на від’ємних частотах є дзеркальним відображенням на додатних частотах.
2. 
W(w)=a(w)+jb(w)
-W(w)=-a(w)-jb(w)
Кожне значення АФЧХ розвернуте на π (180 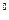 ) відносно початку координат (рис.).
) відносно початку координат (рис.).
3.
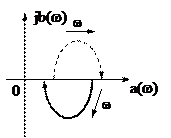 |
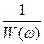
Від’ємна АФЧХ та обернена АФЧХ використовуються в методі гармонічного балансу для дослідження нелінійних систем управління (рис.).
2.9. Логарифмічна амплітудо-фазо-частотна характеристика (ЛАФЧХ)
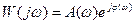
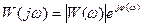
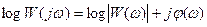
Зручніше користуватись десятковим логарифмом і будувати окремо логарифмічно-амплітудну і фазову характеристики.
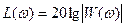 – одиниці вимірювання дБ (децибел)
– одиниці вимірювання дБ (децибел)
1 Бел представляє собою логарифмічну одиницю, що відповідає десятикратному збільшенню потужності.
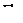      |
ДБ – 1/10 частина Бела. Оскільки модуль W(w) є відношення вхідних і вихідних величин, а не потужностей, то збільшення цього відношення в 10 разів відповідає збільшенню потужності в 100 разів, що відповідає 2 Бел або 20 дБ.
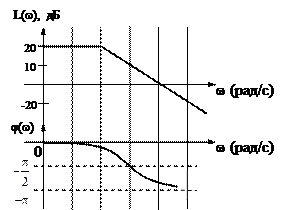
Рис. 2.18.
Особливість логарифмічної характеристики, зображеної на рис. 2.18, полягає в тому, що вона відображається сукупністю відрізків прямої.
2.10. Передатні функції типових ланок
Типовою ланкою називається ланка, яка описується диференційним рівнянням не вище другого порядку.
Дата добавления: 2015-07-24; просмотров: 1047;
