Следствия

1.1. Каждое множество является подмножеством самого себя: A Ì А.

1.2. Пустое множество является подмножеством любого множества A: Æ Ì A.

Множества A и Æ называют несобственными подмножествами множества A, все остальные – собственными подмножествами множества A.

Пусть А и В — некоторые множества.

Определение 1.1. Объединением двух множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств. Обозначается: АÈВ.

На рис. 1 показано объединение множеств А и В при помощи диаграммы Эйлера–Венна.

Рис. 1

Прежде, чем рассмотреть примеры объединения множеств, заметим, что согласно определению объединения х Î А È В Û х Î А ˅ х Î В.

Свойства объединения множеств

Из определения следует, что в А È А входят те же самые элементы, т.е. А È А = А. Вообще, когда B Ì A, то А È В = А. В частности, А È Æ = А.

Операция объединения подчиняется переместительному закону:

А È В = В È А.

Операцию объединения можно распространить на любое число множеств. Когда А, В, С — три произвольные множества, то (А È В)È С есть множество элементов, каждый из которых принадлежит хотя бы одному из множеств А, В, С.

В общем случае объединение совокупности множеств 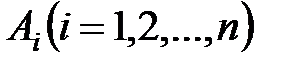обозначается 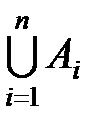и состоит из элементов, принадлежащих хотя бы одному из множеств .

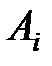Операция объединения подчиняется сочетательному закону:

(А È В)È С = А È (В È С).

Определение 1.2. Пересечением множеств A и B называется множество, состоящее их тех и только тех элементов, которые одновременно принадлежат множествам A и B. Обозначается: АÇВ.

Согласно определению пересечения х Î АÇ В Û х Î А ˄ х Î В.

Пересечение множеств А и В иллюстрируется на рис. 2.

Рис. 2

Свойства пересечения множеств

Очевидно, что А Ç А = А; вообще, когда В Ì А, то В Ç А = В. Из определения пересечения следует: А Ç В = В Ç А, т.е. операция пересечения коммутативна.

Имеет место и следующее равенство: А Ç Æ = Æ.

Операцию пересечения легко распространить и на случай больше двух множеств. Рассмотри три множества А, В, С. Пересечение А Ç В есть множество общих элементов множеств А и В, поэтому (А Ç В) Ç С есть множество элементов, принадлежащих одновременно трём множествам А, В, С.

Аналогично определяется и операция пересечения любого числа множеств. Из приведенного правила пересечения трех множеств следует, что операция пересечения ассоциативна: (А Ç В) Ç С = А Ç (В Ç С). Поэтому используется запись А Ç В Ç С. В общем случае пересечение совокупности множеств 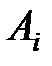(i = 1, 2, …, n) обозначается 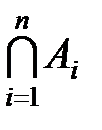и состоит из элементов, принадлежащих сразу всем множествам , .

Заметим, что относительно двух операций пересечения и объединения множеств выполняются два дистрибутивных (распределительных) закона:

1) (А Ç В) È С = (А È С) Ç (В È С);

2) (А È В) Ç С = (А Ç С) È (В Ç С).

Докажем второй из этих законов (первый доказывается аналогично).

Пусть х Î (А È В) Ç С. Значит, х Î А È В и х Î С. Из того, что х Î А È В, следует, что обязательно выполняется по крайней мере одно из двух утверждений: х Î А или х Î В. Когда х Î А, то из того, что х Î С, следует, что х Î А Ç С. Значит, х Î (А Ç С) È (В Ç С). Когда же х Î В, то из того, что х Î С, следует, что х Î В Ç С, но тогда х Î (А Ç С) È (В Ç С).

Таким образом, любой элемент множества (А È В) Ç С является элементом и множества (А Ç С) È (В Ç С).

Докажем теперь обратное. Пусть х Î (А Ç С) È (В Ç С). Возможен один из случаев: х Î А Ç С или х Î В Ç С, т.е. х Î А и х Î С, или х Î В и х Î С. Отсюда получаем, что х Î С и х Î А È В, а это свидетельствует о том, что х Î (А È В)Ç С. Таким образом, второй дистрибутивный закон доказан полностью.

Определение 1.3. Разностью двух множеств A и B называется множество, состоящее из тех и только тех элементов множества A, которые не принадлежат В. Обозначается: А \ В.

Согласно определению разности х Î А \ В Û х Î А ˄ х Ï В.

Графическое изображение разности А \ В множеств А и В показано на рисунке 3 (заштрихованная область — это А \ В).

Рис. 3

Из определения разности следует, в частности, что А \ А = Æ; А \ В ¹ В \ А.

Определение 1.4. Если множество B является подмножеством множества A, то разность множеств A и B называется дополнением множества B до множества A. Обозначается:

А \ В=С_АВ или 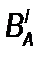или

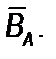
Графическое изображение дополнения 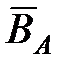множества В до множества А показано на рис. 4.

Рис. 4