ЗАГАЛЬНА ОЦІНКА МОДЕЛЕЙ РУХУ ПОТОКУ АВТОМОБІЛІВ

Не дивлячись на різні підходи до розробки математичних моделей руху потоків автомобілів, між ними багато спільного.

Так, наприклад, існує тісний зв'язок між динамічними моделями. Теоретичні дослідження, проведені Ф. Хейтом, показали, що розв’язування рівнянь теорії “слідування за лідером” приводить до кінцевого рівняння гідродинамічної моделі.

На близькість всіх динамічних моделей також вказує те, що за допомогою кожної з них можна побудувати основну діаграму руху потоку автомобілів: “інтенсивність-щільність” (див. рис. 2.4), у якій зв'язані між собою всі основні характеристики руху потоку автомобілів. За допомогою діаграми “інтенсивність-щільність” можна визначити: швидкість, щільність, інтенсивність, швидкість поширення ударної хвилі тощо. Частина кривої, розташована ліворуч від лінії I—I, відповідає нормальним умовам руху без утворення заторів, права частина кривої — руху автомобілів при виникненні заторів.

Згідно цієї залежності середня швидкість руху визначається як частка від ділення інтенсивності руху N (авт/год) на щільність q (авт/км).

Іншими словами, тангенс кута нахилу радіус вектора 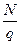дорівнює середній швидкості руху потоку автомобілів. Максимальна інтенсивність, одержана з діаграми, відповідає пропускній здатності розглянутої ділянки дороги. Тангенс нахилу дотичної до кривої “інтенсивність-щільність” дорівнює швидкості поширення хвилі в потоці автомобілів.

Крім зазначених характеристик руху потоку автомобілів на діаграмі, можна також оцінити середню величину інтервалу в часі між автомобілями, які рухаються один за одним 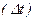і інтервал у часі між заднім буфером переднього автомобіля та переднім буфером заднього автомобіля .

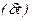Ці інтервали в часі визначаються за формулами:

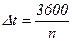; (3.1)

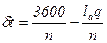, (3.2)

де n – інтенсивність руху, авт/год;

q – щільність руху, авт/км;

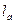- середня довжина автомобіля, м.

Загальний вигляд рівняння “інтенсивність-щільність”, отриманого на основі рівняння теорії “слідування за лідером”, наступний:

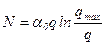. (3.3)

Це рівняння ідентичне з рівнянням Грінберга при 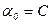, яке отримано за допомогою гідродинамічної моделі.

У рівнянні (3.3) 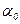- характерна швидкість руху потоку автомобілів на розглянутій ділянці дороги. Ця швидкість визначається на основі аналізу взаємодії двох автомобілів, що рухаються один за одним на цій ділянці дороги.

Крива “інтенсивність-щільність” може бути також отримана за допомогою рівнянь III роду спрощеної динамічної моделі руху потоку автомобілів, яке розв’язується відносно швидкості з використанням рівняння зв'язку: .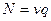

На тісний зв'язок між собою динамічних теорій вказує те, що з рівняння III роду спрощеної динамічної моделі можна отримати одне з рівнянь теорії “слідування за лідером”.

Після диференціювання обох частин рівняння (1) отримаємо:

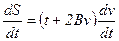(3.4)

або

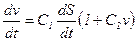. (3.5)

Рівняння (3.5) може бути розглянуте як рівняння теорії “слідування за лідером” з “чутливістю”:

.

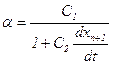Отже, незважаючи на різний підхід до знаходження основного рівняння руху потоку автомобілів, кінцеві результати всіх динамічних теорій (за винятком газової) схожі між собою. Це вказує на можливе існування однієї комплексної динамічної теорії руху потоку автомобілів.

Дослідження динамічних теорій в наш час можливе лише на основі проведення широких натуральних спостережень за рухом потоків автомобілів різних за складом, що рухаються в різних дорожніх умовах.

Незважаючи на детальну розробку окремих теорій, все ж практичне їх застосування дуже обмежене, внаслідок трудомісткості обчислювальних робіт. Використання ПК дозволить розширити практичне використання математичних моделей.

Найбільш важливе практичне застосування моделі руху потоку автомобілів знаходиться при визначенні пропускної здатності автомобільних доріг і їх елементів. В окремих випадках пропускна здатність може бути визначена тільки за допомогою математичних моделей руху потоків автомобілів.

Для оцінки пропускної здатності можуть бути використані як динамічні, так і ймовірнісні моделі.

Ймовірнісні моделі використовуються для оцінки пропускної здатності ділянок автомобільних доріг, де відбувається взаємодія потоків автомобілів, що рухаються по різних смугах: перетинах в одному рівні, ділянках злиття та переплетеннях потоків. У цьому випадку ймовірнісна модель використовується для оцінки кількості граничних інтервалів - інтервалів, які приймаються водіями при перетині потоку автомобілів, при злитті або при зміні смуг руху. Величина граничного інтервалу визначається експериментальним шляхом. По кількості граничних інтервалів і часу, необхідного для здійснення маневру злиття, переплетення або перетинання, визначається пропускна здатність.

Ймовірнісні моделі не можуть бути використані для оцінки пропускної здатності дороги, тому що вони описують тільки рідкі потоки автомобілів. У цьому випадку можуть бути застосовані тільки динамічні моделі руху потоків автомобілів. При цьому або по кривій “інтенсивність-щільність”, або по кривій “інтенсивність-швидкість” визначається максимальна інтенсивність руху, що відповідає пропускній здатності. Потік автомобілів розглядається як неперервний.