ТЕОРІЇ РУХУ ПОТОКІВ АВТОМОБІЛІВ

Першими моделями, які були запропоновані для опису потоку автомобілів, були спрощені динамічні моделі. Ці моделі побудовані на припущенні, що автомобілі рухаються в колоні один за одним з однаковою швидкістю на відстані, достатній для повної зупинки, без наїзду на автомобіль, який йде попереду.

Всі рівняння спрощеної динамічної моделі на різних початкових умовах, можна розділити на наступні групи: І група – рівняння, у яких не враховується гальмівний шлях (рис. 2.1); ІІ група – рівняння, у яких враховується повний гальмівний шлях (рис. 2.2); ІІІ група – рівняння, у яких враховується різниця в гальмівних шляхах заднього та переднього автомобілів (рис. 2.3); ІV група – рівняння, одержані в результаті статистичної обробки даних спостережень за зміною відстані між автомобілями при різних швидкостях руху.

Збільшення швидкості та інтенсивності руху на дорогах, а також збільшення кількості дорожно-транспортних пригод, що стали наслідком зіткнення автомобілів між собою, привели до необхідності більш детального вивчення взаємодії автомобілів, що рухаються один за одним. Була розроблена теорія «руху за лідером», яка є подальшим розвитком спрощених динамічних моделей.

Першим та основним диференціальним рівнянням теорії «руху за лідером» є рівняння наступного вигляду:

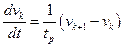(2.1)

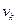де і 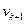- швидкості заднього та переднього автомоділів, м/с;

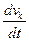- прискорення заднього автомобіля, м/с²;

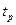- час реакції водія, с

Одержане правило може формулюватись наступним чином: при слідуванні двох автомобілів один за одним на достатньо близькій відстані, коли відбувається їх взаємний вплив, прискорення заднього автомобіля прямо пропорційне різниці швидкостей переднього і заднього автомобілів (відносній швидкості).

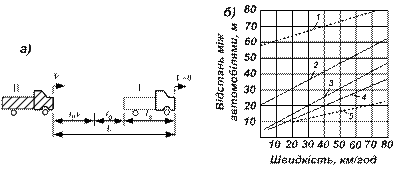
Рис. 2.1. Порівняльна оцінка результатів, які одержані на основі спрощених динамічних рівнянь І групи: а – розрахункова схема руху автомобілів; б – залежність мінімальної відстані між автомобілями від швидкості руху за даними: 1 – Гуревича; 2 – Даденкова; 3 – Швантера; 4 – Йоганнесона; 5 – Гріншильдса.

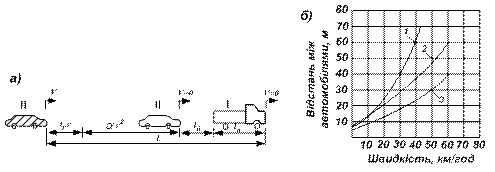
Рис. 2.2. Порівняльна оцінка спрощених динамічних рівнянь ІІ групи: а – розрахункова схема руху автомобілів; б – залежність мінімальної відстані між автомобілями від швидкості руху за даними: 1 – Страментова; 2 – Крилова; 3 – Льюіса

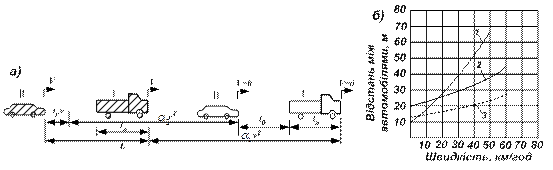
Рис. 2.3. Порівняльна оцінка спрощених динамічних рівнянь ІІІ групи: а - розрахункова схема руху автомобілів; б – залежність мінімальної відстані між автомобілями від швидкості руху за даними: 1 – Веліканова; 2 – Писарєва; 3 – Полякова.

Останні дослідження дозволили одержати рівняння теорії «руху за лідером» у загальному вигляді:

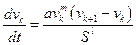, (2.2)

де а – коефіцієнт пропорційності;

S – відстань між автомобілями;

m і l – коефіцієнти.

Це рівняння використано для дослідження «локальної» та «асимптичної» стійкості руху потоку автомобілів після внесення збурення в потік та для оцінки безпеки руху. Локальна стійкість характеризує відносне положення заданої пари автомобілів, а асимптична – затухання або посилення амплітуди збурення при розповсюдженні його вздовж колони автомобілів.

Теоріями, які дозволяють дати загальну оцінку стану потоку автомобілів є: гідродинамічні та газові.

Відомі дві гідродинамічні теорії, побудовані на використанні: перша – рівняння нерозривності та друга – понятті про «потенціал тиску».

Рівняння нерозривності побудоване на принципах закону збереження мас. При розгляді потоку автомобілів приймається до уваги сталість загальної кількості автомобілів на ділянці дороги.

Основне рівняння нерозривності має вигляд:

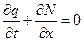(2.3)

Суть цього рівняння наступна: кількість автомобілів, що входять в момент 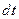на ділянку 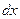, дорівнює кількості автомобілів, що виходять з цієї ділянки.

Гідродинамічна теорія використовується для опису утворення хвилі в потоці автомобілів та оцінки пропускної здатності. Ці характеристики визначаються за основною діаграмою руху потоку автомобілів «інтенсивність-щільність» (рис. 2.4).

Рис. 2.4. Загальний вид кривої «інтенсивність - щільність»: 1 – радіус-вектор середньої швидкості 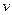; 2 – радіус-вектор швидкості поширення ударної хвилі .

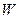Гідродинамічна модель, яка грунтується на використанні «потенціалу тиску» базується на припущенні, що рух автомобіля виражається у вигляді функції деякого «потенціалу тиску», який залежить від дорожніх умов та стану водія. Рух потоку автомобілів моделюється рівнянням руху потоку в’язкої рідини. Дорожні умови оцінюються параметром 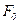, який визначається на основі спостережень за швидкостями руху:

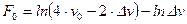, (2.4)

де 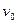- швидкість руху при вільних умовах;

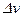- пониження швидкості на окремих геометричних елементах.

Газова теорія дозволяє моделювати рух потоку автомобілів на багатосмугових дорогах при вільних умовах руху.

Основною функцією, яка характеризує рух потоку автомобілів, є функція розподілу швидкостей руху 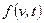. Практичне використання цієї теорії грунтується на визначенні фактичних кривих розподілу швидкостей руху при різних дорожніх умовах.

Для опису руху потоків автомобілів низької інтенсивності використовуються методи теорії ймовірностей. Найпоширеніше застосування набув розподіл Пуассона:

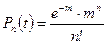, (2.5)

де 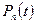- ймовірність прибуття на певний переріз дороги 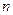автомобілів напротязі часу ;

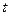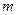- середня кількість автомобілів, що прибувають за час 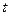, тобто ;

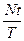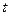- тривалість інтервалу спостереження, с.;

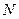- кількість автомобілів, що проходить за час 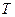. Зазвичай 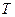приймають рівним 1 година = 3600 с.

Ймовірність того, що за час 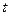не пройде жоден автомобіль, рівна:

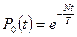(2.6)

Із характеристик потоку, який взято за основу при виведенні рівняння Пуассона, видно, що ця закономірність найповніше описує рух потоків, які складаються з однотипних автомобілів з низькою щільністю руху.

Поява різного роду перешкод руху та зміна складу потоку автомобілів приводить до неможливості застосування розподілу Пуассона. Тому були запропоновані поправки до цього рівняння, де враховується, що потік складається з двох груп автомобілів (зв’язаних і тих, які рухаються вільно), кожна з яких описується рівнянням Пуассона:

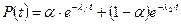(2.7)

де 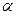- кількість «зв’язаних» автомобілів;

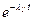і 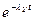- ймовірність появи інтервалів визначеної довжини у зв’язаних і вільних частинах потоку автомобілів.

Для опису руху потоку автомобілів у характерних умовах можуть використовуватись також ланцюги Маркова, гама-розподіли, біноміальні розподіли тощо.