Реализация булевых функций
Пусть логическая функцияот трех переменных: М = f(А, В, С), задана следующей таблицей истинности:
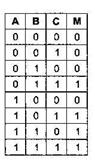
Это функция большинства, которая принимает значение:
· 0, если большинство переменных равны 0,
· 1, если большинство переменных равны 1.
Дизъюнктивная нормальная форма(ДНФ) заданной функции имеет вид:
 |
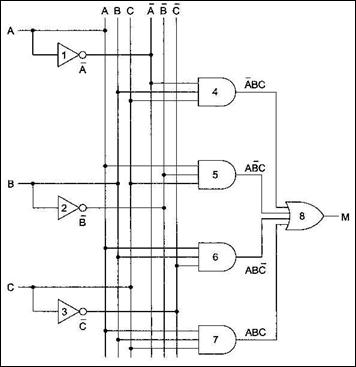Реализация этой функции в виде логической схемы показана на рисунке:
Входные сигналы А, В и С показаны с левой стороны, а функция М, полученная на выходе, — с правой. Поскольку необходимы дополнительные величины (инверсии) входных переменных, для их получения сигнал проходит через инверторы 1, 2 и 3.
Чтобы сделать рисунок понятней, нарисованы 6 вертикальных линий, 3 из которых связаны с входными переменными, 3 другие — с их инверсиями.
Эти линии обеспечивают передачу входного сигнала к вентилям. Например, вентили 5, 6 и 7 на входе получают сигнал А. В реальной схеме эти вентили будут непосредственно соединены проводом с А без каких-либо промежуточных вертикальных проводов.
Схема содержит четыре вентиля И, - по одному по одному для каждой строки в таблице истинности с результатом 1, или по одному для каждого минитерма ДНФ функции М.
Каждый вентиль И вычисляет одну из указанных строк таблицы истинности или один минитерм ДНФ функции М.
Для получения конечного результата выходы каждого вентиля И соединены с входами вентиля ИЛИ.
Общий алгоритм построения логической схемы для любой булевой функции, заданной таблицей истинности, включает следующие шаги:
1. Составить ДНФ для данной функции (дизъюнкция минитермов, каждый из которых является конъюнкцией всех входных переменных (или их отрицаний) и соответствует строке таблицы истинности с единичным результатом).
2. Включить в схему инверторы, для каждой переменной (входного сигнала), входящей в ДНФ с отрицанием.
3. Нарисовать вентиль И для каждого минитерма ДНФ
4. Соединить вентили И с соответствующими входными сигналами.
5. Вывести выходы всех вентилей И и направить их на вход вентиля ИЛИ.
Этот алгоритм позволяет реализовать любую булеву функцию с помощью вентилей НЕ, И и ИЛИ.
 |
Например. Схемная реализация "Сожжения по модулю два" (исключительное ИЛИ)
Однако часто удобнее строить схемы с использованием одного типа вентилей. Для этого можно преобразовать схемы, построенные по рассмотренному алгоритму, в форму НЕ-И или НЕ-ИЛИ.
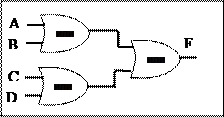
Для этого нужно реализовать вентили НЕ, И и ИЛИ с помощью какого-нибудь одного типа вентилей. Один из способов такого преобразования с использованием вентиля НЕ-И или НЕ-ИЛИ показан на рисунке:
 |
Для того чтобы реализовать булеву функцию только на базе вентиля НЕ-И или НЕ-ИЛИ, можно сначала следовать описанному алгоритму, сконструировав схему с вентилями НЕ, И и ИЛИ. Затем нужно заменить многовходовые вентили эквивалентными схемами на двухвходовых вентилях.
 |
Например.
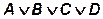можно поменять на 
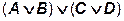, использовав три двухвходовых вентиля.
 |
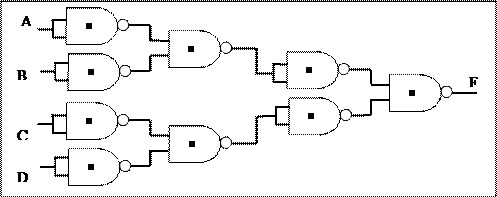Затем каждый двухвходовый вентили НЕ, И иИЛИ заменяется соответствующей схемой, реализованной на базе только одного типа вентилей, например НЕ-И.
Хотя такая процедура и не приводит к схемам с минимальным количеством вентилей, она показывает возможность подобного преобразования.
Вентили НЕ-И и НЕ-ИЛИ считаются функционально полными, потому что каждый из них позволяет вычислить любую булеву функцию.
Ни одни другой вентиль не обладает таким свойством, Поэтому именно эти два типа вентилей предпочтительнее при построении логических схем.
Дата добавления: 2015-07-24; просмотров: 2220;