Разветвленная цепь однофазного переменного тока. Резонанс токов

Рассмотрим разветвленную цепь, параллельно соединённых катушки индуктивности L (с активным сопротивлением R) и конденсатора С (рис. 2.29).

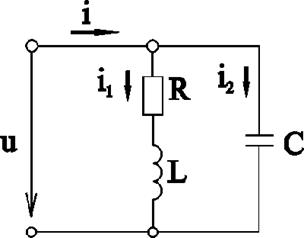
Рис.2.29. Электрическая схема разветвлённой цепи

Пусть мгновенные значения напряжения и тока цепи изменяются по синусоидальному закону 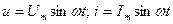. По первому закону Кирхгофа 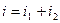, для действующих значений токов 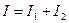. По закону Ома 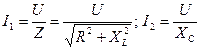. Из треугольника сопротивлений, для последовательно соединённых R и L, 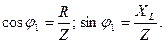Разложим токи в ветвях на активные и реактивные составляющие IR, IL, IC и определим их значения: .

Введем следующие обозначения:

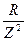=g (2.25)

- активная проводимость первой ветви;

(2.26)

- реактивная индуктивная проводимость первой ветви;

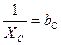(2.27)

- реактивная емкостная проводимость второй ветви.

Для случая IL > IC построим векторную диаграмму (рис. 2.30):

Из векторной диаграммы находим общий ток:

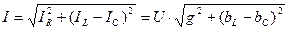, (2.28)

где

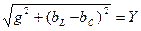(2.29)

- полная проводимость цепи.

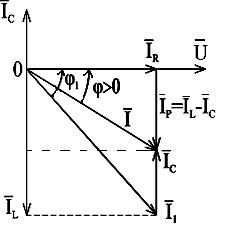
Рис.2.30. Векторная диаграмма разветвлённой цепи переменного тока

Из векторной диаграммы следует, что наличие ёмкости снизило вектор действующего значения тока 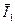до величины 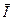, а cosφ при этом увеличился. Резонанс токов можно практически получить изменением ёмкости конденсатора. На рис.2.31 приведены примерные графические зависимости IL, IC, I, cosφ от изменения C, где Cp - резонансная ёмкость.

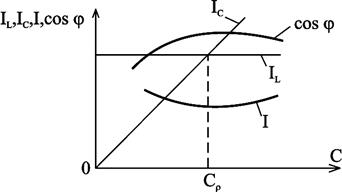
Рис.2.31. Примерное изображение зависимостей IL, IC, 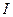, cos 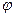от изменения ёмкости конденсатора C

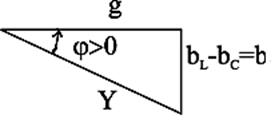
Рис.2.32. Треугольник проводимостей цепи

Выражение (2.29) соответствует треугольнику проводимостей цепи, представленному на рис. 2.32, откуда следует:

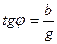; (2.30)

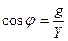. (2.31)

Выражения для мощностей принимают такой вид:

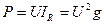(2.32)

- активная мощность,

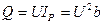(2.33)

- реактивная мощность,

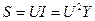(2.34)

- полная мощность.

Резонансом токов для рассматриваемой цепи называют явление, при котором ток IL = IC , тогда общий ток I в неразветвленной части цепи совпадает по фазе с напряжением источника. При резонансе токов 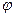= 0; cos 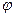= 1; bL = bC; I = IR. Пусть резонансная частота f0 определяется из соотношения 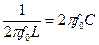, тогда 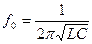, а угловая резонансная частота .

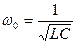Итак, признаками резонанса токов являются:

а) индуктивная и емкостная проводимости равны;

б) ток в неразветвленной части цепи совпадает по фазе с напряжением источника и имеет минимальное значение;

в) коэффициент мощности максимален.