Цепь переменного тока с индуктивностью

Пусть в цепи переменного тока (рис 2.15) с индуктивной катушкой L без ферромагнитного сердечника проходит синусоидальный ток i= 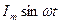(рис.2.16).

В результате, вокруг катушки возникает магнитное поле, и в катушке наводится ЭДС самоиндукции 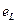. При r = 0 напряжение источника - .

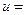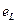Так как 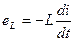, тогда

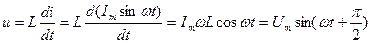. (2.12)

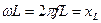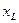Пусть , где - индуктивное сопротивление.

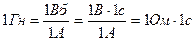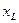
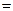
Действительно, если индуктивность в , то индуктивное сопротивление 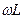измеряется в Омах, если 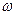измеряется в .

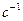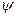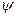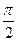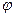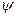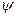Сопоставляя выражения для мгновенных значений тока и напряжения в цепи с индуктивностью, имеем: i = 0; u = , откуда угол сдвига фаз = u - i = .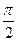

Рис.2.15. Цепь переменного тока с индуктивностью

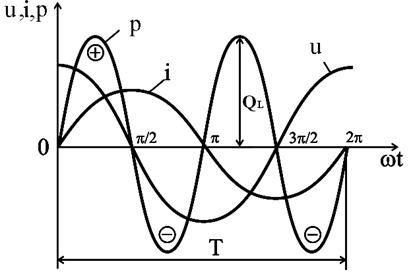
Рис.2.16. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с индуктивностью

Рис.2.16 показывает, что ток в цепи с индуктивностью отстаёт от напряжения на угол 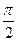. Для действующих значений напряжения и тока 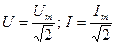, тогда закон Ома для рассматриваемой цепи имеет выражение

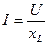, (2.13)

а векторные диаграммы в векторном и комплексном виде представлены на рис. 2.17.

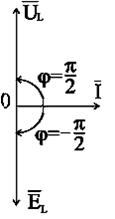
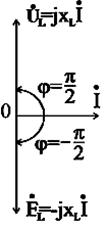
Рис.2.17. Векторные диаграммы действующих значений тока и напряжения цепи переменного тока с индуктивностью в векторном и комплексном виде

Мгновенная мощность цепи переменного тока с индуктивностью 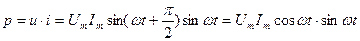. Так как 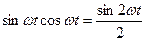и 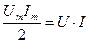, то окончательно имеем:

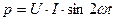(2.14)

Следовательно, p является переменной величиной, изменяющейся синусоидально с частотой вдвое больше частоты переменного тока (рис.2.16). Четверть периода мгновенная мощность положительна, четверть периода отрицательна.

При положительном значении мощности мгновенный ток возрастает и происходит накопление энергии магнитного поля индуктивности. При отрицательном значении мощности мгновенный ток уменьшается и энергия, накопленная в индуктивности, возвращается к источнику. Таким образом, в цепи с индуктивностью происходит обмен энергии между источником и магнитным полем индуктивности без затраты энергии источника, то есть средняя мощность или активная мощность P = Pср = 0.

Для количественной характеристики интенсивности обмена энергией между источником и катушкой служит реактивная индуктивная мощность, равная амплитуде колебаний:

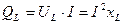. (2.15)

Единицей реактивной индуктивной мощности является вольт-ампер реактивный (вар).

2.5. Цепь переменного тока с ёмкостью

Проанализируем процессы в цепи переменного тока, представленной на рис.2.18. Зададимся напряжением на зажимах источника 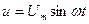, тогда ток в цепи с ёмкостью так же будет меняться по синусоидальному закону. Ток определяется по формуле 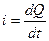. Количество электричества Q конденсатора связано с напряжением на ёмкости и его ёмкостью: 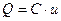. Следовательно,

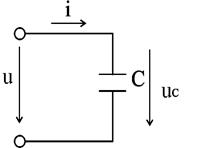
Рис.2.18. Цепь переменного тока с ёмкостью

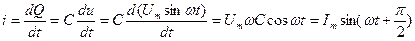(2.16)

Таким образом, ток в цепи с ёмкостью опережает по фазе напряжение на угол 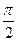(рис. 2.19).

Рис.2.19. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с ёмкостью

Сопоставляя значения для мгновенного тока и напряжения в цепи с ёмкостью, из рис.2.19 имеем: 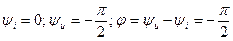. Из формулы (2.16) выведем закон Ома для амплитудных значени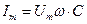й: или

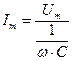. (2.17)

Введем обозначени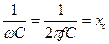е: , где 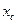- емкостное сопротивление.

Действительно, если ёмкость в , то 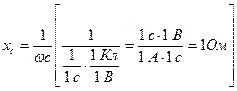измеряется в Омах.

Закон Ома для действующих значений напряжения 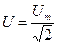и тока 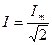имеет выражение:

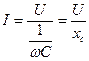. (2.18)

Для комплексных чисел закон Ома записывается в виде

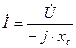. (2.19)

Диаграммы в векторном и комплексном видах представлены на рис. 2.20.

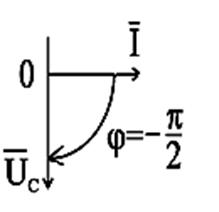
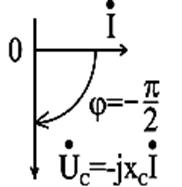
Рис.2.20. Векторные диаграммы действующих значений тока и напряжения цепи переменного тока с ёмкостью в векторном и комплексном виде

Так как напряжение на ёмкости отстает от тока на угол 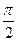, который изменяется по косинусоиде, то мгновенную мощность выразим в виде:

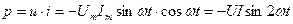, (2.20)

где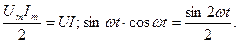

Мгновенная мощность p имеет частоту 2ω, но в отличие от индуктивности, здесь мощность положительна, пока возрастает напряжение на ёмкости. Происходит накопление энергии электрического поля на конденсаторе. Затем конденсатор разряжается на источник, и мощность становится отрицательной.

Из рис. 2.19 видно, что средняя или активная мощность P = Pср= 0. Амплитуда колебаний мощности в цепи с ёмкостью называют реактивной емкостной мощностью:

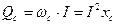. (2.21)

Единицей реактивной емкостной мощности является вольт-ампер реактивный (вар).