Молекулярная физика (№№ 201-230)
Пример 1.Определить число молекул в 1 мм3 воды и массу одной молекулы воды.
Решение. Число N молекул, содержащихся в массе m вещества, имеющего молярную массу 
, равно числу Авогадро NA, умноженному на число молей n = m/ :
.
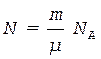Масса вещества определяется как 
, следовательно,
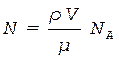, (1)
где 
- плотность воды.
После подстановки числовых значений в формулу (1) имеем
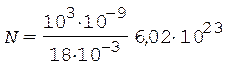= 3,34×1019 молекул.
Массу mо одной молекулы воды можно определить, разделив массу одного моля на число Авогадро:
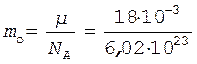= 2,99×10-26 кг.
Пример 2. Найти среднюю кинетическую энергию 
вращательного движения молекулы водорода при температуре t°= 27 °С и кинетическую энергию Евр вращательного движения всех молекул водорода массой m = 2 г.
Решение. В соответствии с теоремой о равномерном распределении энергии по степеням свободы на каждую степень свободы молекулы приходится энергия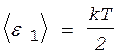 
. Вращательному движению двухатомной молекулы соответствуют две степени свободы. Следовательно, средняя энергия вращательного движения молекулы водорода равна
. (1)
Произведем вычисления:
=1,38×10-23×300=4,14×10-23 Дж.
Кинетическая энергия вращательного движения всех молекул газа вычисляется по формуле
, (2)
где N - число всех молекул газа, равное N = NAn;
NA -число Авогадро;
n - количество вещества.
Учтем, что количество вещества n = m/m, где m - масса газа; m - молярная масса газа. Тогда выражение N = NAn примет вид
.
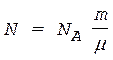Подставим это выражение в формулу (2):
.
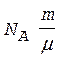Произведем вычисления, учитывая, что молярная масса водорода m = 2×10-3 кг/моль:
= 4,14×10-21×6,02×10-23× 
= 24,9×102 Дж.
Пример 3.Газообразный кислород массой m = 10 г находится под давлением p1= 3×105 Па при темпера-туре 
= 10 °С. После расширения вследствие нагре-вания при постоянном давлении газ занял объем V = 10 л. Найти объем и плотность газа до расшире-ния, температуру и плотность газа после расширения.
Решение. Для нахождения объема кислорода до расширения воспользуемся уравнением состояния газа (уравнением Менделеева-Клапейрона) и учтем, что молярная масса кислорода m = 32×10-3 кг/моль:
.
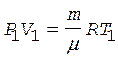Тогда
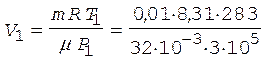= 2,4×10-3 м3.
Плотность кислорода до расширения равна
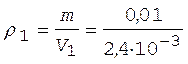= 4,14 кг/м3.
Температуру кислорода после расширения можно найти, применив закон Гей-Люссака:
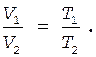(1)
Из выражения (1) следует:
Плотность кислорода после расширения равна
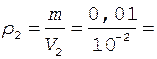1 кг/м3.
Дата добавления: 2015-07-24; просмотров: 790;