Пусть имеем функцию двух переменных
z = f(х, у).
Частные производные 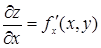 и
и 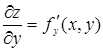 , вообще говоря, являются функциями переменных х и у. Поэтому от них можно снова находить частные производные. Следовательно, частных производных второго порядка от функции двух переменных четыре, так как каждую из функций
, вообще говоря, являются функциями переменных х и у. Поэтому от них можно снова находить частные производные. Следовательно, частных производных второго порядка от функции двух переменных четыре, так как каждую из функций 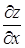 и
и 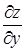 можно дифференцировать как по х, так и по у.
можно дифференцировать как по х, так и по у.
Вторые частные производные обозначаются так:
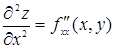 , ,
| здесь f дифференцируется последовательно два раза по х; |
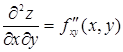
| здесь f сначала дифференцируется по х, а потом результат дифференцируется по у; |
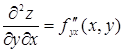
| здесь f сначала дифференцируется по у, а потом результат дифференцируется по х; |
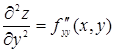
| здесь f дифференцируется последовательно два раза по у. |
Производные второго порядка можно снова дифференцировать как по х, так и по у. Получим частные производные третьего порядка. Их будет, очевидно, уже восемь:
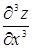 ,
, 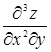 ,
, 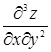 ,
, 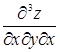 ,
, 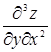 ,
, 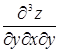 ,
, 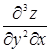 ,
, 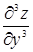 .
.
Вообще, частная производная п-го порядка есть первая производная от производной (п – 1)-го порядка. Например, 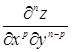 есть производная п-го порядка; здесь функция z сначала р раз дифференцировалась по х, а потом п – р раз по у.
есть производная п-го порядка; здесь функция z сначала р раз дифференцировалась по х, а потом п – р раз по у.
Для функции любого числа переменных частные производные высших порядков определяются аналогично.
Пример 28. Вычислить частные производные второго порядка от функции 
Решение. Последовательно находим
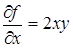 ,
, 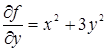 ,
, 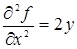 ,
, 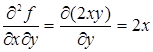 ,
, 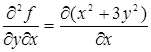 ,
, 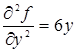 .
.
Пример 29. Вычислить 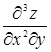 и
и 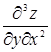 , если
, если 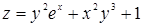 .
.
Решение. Последовательно находим
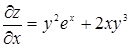 ,
, 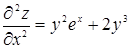 ,
, 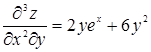 ,
,
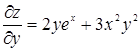 ,
, 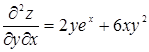 ,
, 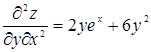 .
.
Пример 30. Вычислить 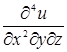 , если
, если 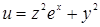 .
.
Решение. 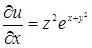 ,
, 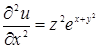 ,
, 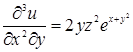 ,
, 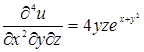 .
.
Естественно поставить вопрос, зависит ли результат дифференцирования функции нескольких переменных от порядка дифференцирования по разным переменным, т.е. будут ли, например, тождественно равны производные
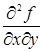 и
и 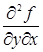
или
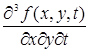 и
и 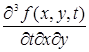 и т.д.
и т.д.
Оказывается, что справедлива следующая теорема.
Теорема. Если функция z = f(х, у) и ее частные производные f¢х, f¢у, f¢¢ху и f¢¢ух определены и непрерывны в точке М(х, у) и в некоторой ее окрестности, то в этой точке
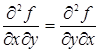 (f¢¢ху = f¢¢ух).
(f¢¢ху = f¢¢ух).
Из данной теоремы как следствие получается, что если частные производные 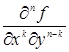 и
и 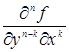 непрерывны, то
непрерывны, то
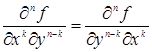 .
.
Аналогичная теорема имеет место и для функции любого числа переменных.
Пример 31. Найти 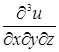 и
и 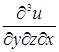 , если
, если 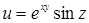 .
.
Решение.
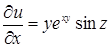 ,
, 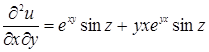 ,
, 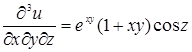 ,
,
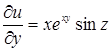 ,
, 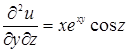 ,
, 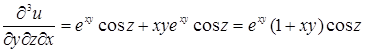 .
.
Следовательно, 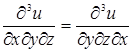 .
.
Дифференциалом второго порядка от функции z = f(х, у) называется дифференциал от его полного дифференциала, т.е. d2z = d(dz).
Аналогично определяются дифференциалы третьего и высших порядков: d3z = d(d2z); вообще dпz = d(dп-1z).
Если х и у – независимые переменные и функция f(х, у) имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам
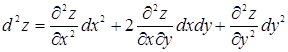 ;
;
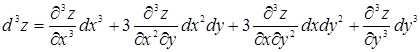 .
.
Вообще, имеет место символическая формула
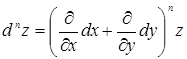 ,
,
которая формально раскрывается по биномиальному закону.
Пример 32. Найти d3z, если z = x2y.
Решение. 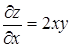 ,
, 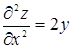 ,
, 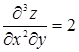 ,
, 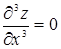 ,
, 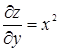 ,
, 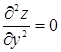 ,
, 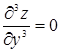 ,
, 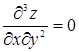 .
.
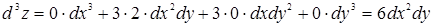 .
.
Дата добавления: 2015-07-24; просмотров: 1151;
