Этапы построения математической модели ЭМ
Построение математической модели ЭМ необходимо выполнить в предлагаемой последовательности.
Этап 1.Используя метод вероятных путей магнитного потока (прил. 1, п. 2), разбить пространство в рабочем воздушном зазоре и прилегающие области на трубки магнитного потока простой геометрической формы так, как условно показано на рис. 1.2.

Рис. 1.2. Схема разбивки рабочего воздушного зазора и прилегающей
области на трубки магнитного потока
На рис. 1.2 условно обозначены стрелками следующие трубки магнитного потока:
А – трубка потока между полюсными торцами магнитопровода а1б1в1г1 и а2б2в2г2 в форме прямой призмы, в основании которой лежит прямоугольник со сторонами аи b, высота призмы – d;
В – трубка потока между ребрами полюсных торцов а1г1 и а2г2 в форме половины прямого кругового цилиндра диаметром d и высотой а;
С – трубка потока между гранями а1г1з1д1 и а2г2з2д2в форме половины прямого кругового полого цилиндра с внутренним диаметром d, толщиной стенки си высотой а;
D – трубка потока между вершинами полюсных торцов а1 и а2 в форме четверти шара диаметром d;
Е – трубка потока между ребрами полюсов а1д1 и а2д2 в форме четверти полой сферической оболочки с внутренним диаметром d и с толщиной оболочки с.
Трубка типа А ограничивает рабочий магнитный поток, остальные (В,С, D и Е) – магнитные потоки рассеяния.
Этап 2. Воспользовавшись формулами для проводимостей трубок магнитного потока, приведенными в прил. 1, п. 3, рассчитать проводимости трубок магнитного потока воздушного зазора ЭМ (рис. 1.2).
Проводимость Ld рабочего воздушного зазора (трубка потока типа А) вычислить по формуле
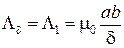 . (1.1)
. (1.1)
Проводимость L2 трубки с основаниями а1г1и а2г2 (трубка потока типа В) вычислить по формуле
L2 = m00,26а. (1.2)
По аналогии проводимость L3 трубки с основаниями а1б1и а2б2вычислить по формуле
L3 = m00,26b. (1.3)
Проводимость L4 трубки с основаниями а1г1з1д1 и а2г2з2д2 (трубка потока типа С) вычислить по формуле
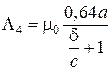 . (1.4)
. (1.4)
По аналогии проводимость L5 трубки с основаниями а1б1е1д1 и а2б2е2д2 вычислить по формуле
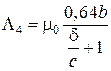 . (1.5)
. (1.5)
Проводимость L6 трубки с основаниями а1 и а2 (трубка потока типа D) вычислить по формуле
L6 = m00,077d. (1.6)
Проводимость L7 трубки с основаниями а1д1 и а2д2 (трубка потока типа Е) вычислить по формуле
L7 = m00,25с. (1.7)
С учетом симметрии формы магнитопровода полную проводимость рассеяния Λрас вычислить по формуле
Lрас = 2(L2 + L3 + L4 + L5) + 4(L6 + L7). (1.8)
Этап 3. Используя методы теории магнитных цепей (прил. 1, п. 1), составить магнитную цепь, моделирующую магнитную систему ЭМ (рис. 1.3).
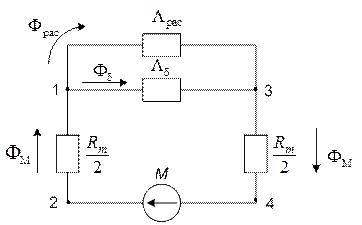
Рис. 1.3. Магнитная цепь, моделирующая магнитную систему ЭМ:
Ld – проводимость воздушного зазора; Lрас – полная проводимость трубок потоков рассеяния воздушного зазора; Rm – магнитное сопротивление магнитопровода;
M – МДС электрической катушки
Используя закон Ома для участка цепи и второй закон Кирхгофа на основании схемы рис. 1.3, можно записать три следующих уравнения:
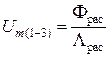 ; (1.9)
; (1.9)
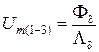 ; (1.10)
; (1.10)
Um(1–2) + Um(1–3) + Um(3–4) = M, (1.11)
где Um(1–2), Um(1–3) и Um(3–4) – магнитные напряжения соответственно на участках 1–2, 1–3, 3–4 магнитной цепи; M – МДС обмотки электрической
катушки.
По определению
M = NI, (1.12)
где I и N – соответственно электрический ток и число витков обмотки электрической катушки ЭМ.
Магнитное сопротивление магнитопровода Rm может быть учтено с помощью кривой намагничивания материала магнитопровода (см. прил. 1, п. 6).
При этом используются следующие соотношения:
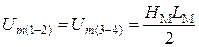 ; (1.13)
; (1.13)
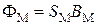 , (1.14)
, (1.14)
где HM и BM – соответственно напряженность магнитного поля и магнитная индукция, являющиеся координатами точки кривой намагничивания, определяющей магнитное состояние материала магнитопровода ЭМ;
LM и SM – соответственно длина и поперечное сечение магнитопровода ЭМ, SM = ab.
С учетом соотношений (1.9), (1.10) и (1.13) уравнение (1.11) можно
записать в виде системы трех уравнений:
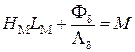 ; (1.15)
; (1.15)
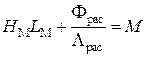 ; (1.16)
; (1.16)
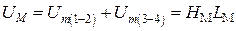 , (1.17)
, (1.17)
где Fd и Fрас – соответственно магнитный поток в рабочем зазоре и магнитный поток рассеяния ЭМ; UM – магнитное напряжение на всем магнитопроводе.
На основании первого закона Кирхгофа для узла 1 (или 3) магнитный поток ΦМ в магнитопроводе равен (см. рис. 1.3):
FМ = Fd + Fрас. (1.18)
Магнитная индукция в рабочем зазоре определяется по формуле
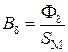 . (1.19)
. (1.19)
Для упрощения математической модели ЭМ примем два следующих допущения:
1) размеры a и b поперечного сечения магнитопровода ЭМ неизменны по всей его длине;
2) окно магнитопровода ЭМ имеет те же размеры, что и поперечное сечение обмотки его электрической катушки.
С учетом сказанного можно записать следующее соотношение для площади окна обмотки электрической катушки ЭМ:
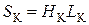 , (1.20)
, (1.20)
где HK и LK – соответственно высота и длина электрической катушки ЭМ.
Минимально допустимая площадь сечения обмотки с учетом наибольшей допустимой плотности тока jдоп должна быть равной:
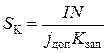 , (1.21)
, (1.21)
где Kзап – коэффициент заполнения сечения катушки обмоточным проводом.
С учетом геометрии магнитопровода (рис. 1.1) можно записать соотношение:
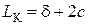 . (1.22)
. (1.22)
Решая совместно систему уравнений (1.20)–(1.22), получим формулу для вычисления высоты катушки:
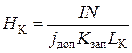 . (1.23)
. (1.23)
Анализ рис. 1.1 позволяет установить, что средняя длина силовой линии магнитопровода равна:
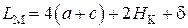 . (1.24)
. (1.24)
Уравнения (1.1)–(1.8), (1.10), (1.12), (1.14)–(1.19), (1.22)–(1.24), а также графики кривой намагничивания материала магнитопровода (прил. 1, п. 6) составляют математическую модель ЭМ.
Полученная математическая модель является нелинейной в связи с нелинейностью кривой намагничивания материала магнитопровода и анализируется графо-аналитическим методом, с применением метода последовательных приближений.
Используя уравнение (1.11) с учетом формул (1.13), (1.14), (1.17) и (1.18), после преобразований получим следующее уравнение:
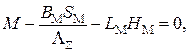 (1.25)
(1.25)
где 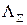 – полная суммарная проводимость трубок потоков рабочего зазора
– полная суммарная проводимость трубок потоков рабочего зазора
с учетом магнитных проводимостей трубок потоков рассеяния.
Значение проводимости 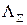 определяется по формуле
определяется по формуле
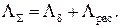 (1.26)
(1.26)
Зависимость между значениями напряженности магнитного потока 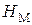 и магнитной индукцией
и магнитной индукцией 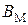 материала магнитопровода обозначим функцией
материала магнитопровода обозначим функцией 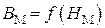 и будем определять по основной кривой намагничивания (прил. 1, п. 6).
и будем определять по основной кривой намагничивания (прил. 1, п. 6).
Полученная нелинейная система уравнений
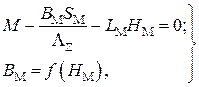 (1.27)
(1.27)
описывает магнитное состояние ЭМ.
Система (2.27) может быть приведена к нелинейному уравнению:
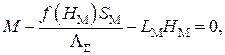 (1.28)
(1.28)
которое решается одним из численных методов, например, методом деления отрезка пополам (прил. 1, п. 7).
Для реализации численного решения указанным методом уравнение (1.28) заменим функцией
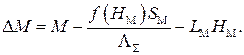 (1.29)
(1.29)
Исследуем функцию (2.29) на монотонность, для чего вычислим ее производную:
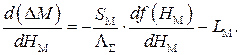 (1.30)
(1.30)
Анализ соотношения (1.30) показывает, что величины 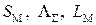 существенно положительные, а производная
существенно положительные, а производная 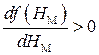 при
при 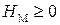 , что следует из анализа основной кривой намагничивания. Поэтому во всей области определения аргумента (
, что следует из анализа основной кривой намагничивания. Поэтому во всей области определения аргумента ( 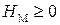 ) производная
) производная 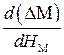 монотонно отрицательна и не имеет особенностей типа «экстремум».
монотонно отрицательна и не имеет особенностей типа «экстремум».
1.2.2. Исследование связи между величиной магнитной индукции Bd
в рабочем зазоре ЭМ и током I в его электрической катушке
при различной степени насыщения материала магнитопровода
Анализ магнитной цепи (рис. 1.3), моделирующей магнитную систему ЭМ, показывает, что магнитная индукция Вd в рабочем воздушном зазоре (магнитный поток Fd) создается за счет электрического тока I в обмотке электрической катушки ЭМ (МДС М). Протекание магнитного потока Fd через рабочий воздушный зазор обусловливает в нем магнитное напряжение Um(1–3), определяемое по формуле (1.10). Через магнитопровод протекает магнитный поток FМ, который обусловливает в нем магнитное напряжение UM, определяемое по формуле (1.17). Магнитное напряжение Um(1–3) является полезной составляющей, так как затрачивается на проведение магнитного потока Fd через рабочий воздушный зазор, а магнитное напряжение UМ характеризует непродуктивные потери МДС на проведение магнитного потока FМ в магнитопроводе.
Для исследования связи между магнитной индукцией Вd и током I с учетом свойств магнитного материала магнитопровода построим алгоритм анализа магнитной системы ЭМ с использованием разработанной математической модели.
Схема такого алгоритма представлена на рис. 1.4. При построении схемы алгоритма использовались сведения, приведенные в прил. 2.
Исходными данными для исследования являются следующие параметры:
1) геометрические размеры ЭМ, м ...................................... а; в; с; d;
2) максимально допустимая по условиям нагрева обмотки электри-ческой катушки плотность тока, А/м 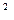 ................................................................. j
................................................................. j 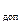 ;
;
3) число витков обмотки электрической катушки, витков ........... N;
4) коэффициент заполнения токопроводящим проводником (как правило, медный или алюминиевый изолированный обмоточный провод) обмоточного окна катушки ,о.е .............................................................................................. K 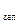 ;
;
5) ток (рекомендованные преподавателем значения) в электрической обмотке катушки, А ................................................................................................ I;
6) основная кривая намагничивания магнитного материала магнитопровода (1 квадрант) ................................................................. графики, прил. 1, п. 6;
7) значение магнитной индукции на выбранной основной кривой намагничивания при напряженности магнитного поля 10 кА/м,Тл ........................ В 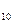 ;
;
8) заданное значение максимальной относительной погрешности определения координат рабочей точки на основной кривой намагничивания материала магнитопровода, о. е. ............................................................................................. g;
9) магнитная постоянная m 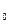 = 4p10
= 4p10 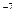 Гн/м.
Гн/м.
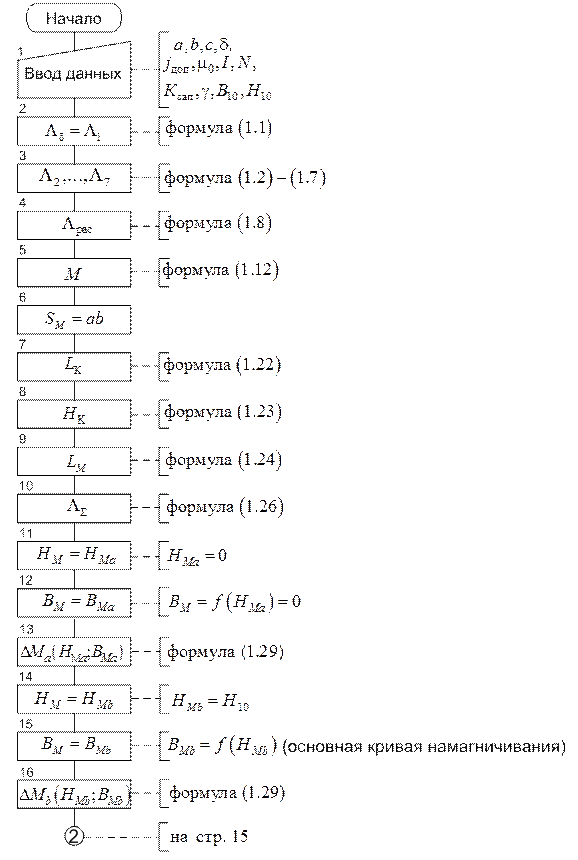
Рис. 1.4. Схема алгоритма анализа ЭМ (см. также с. 15-16)
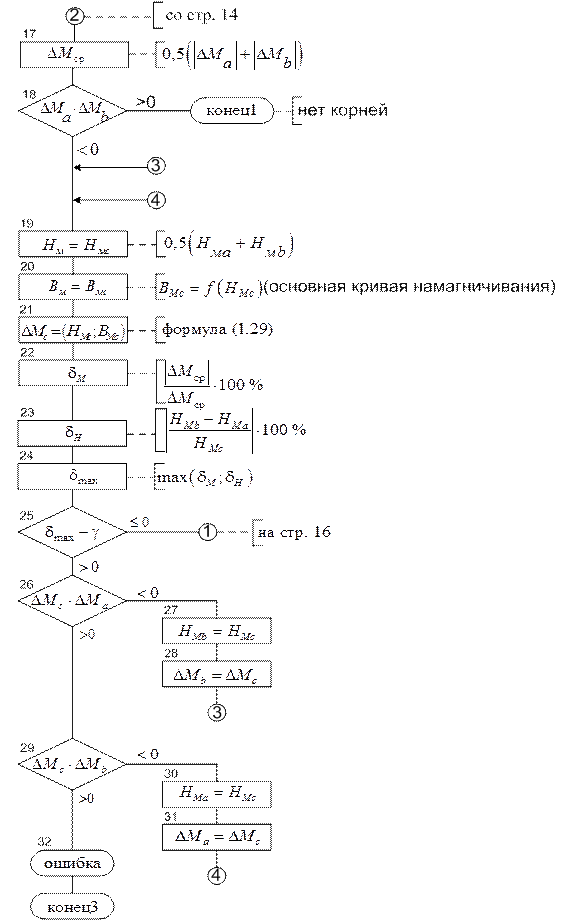
Рис. 1.4. Схема алгоритма анализа ЭМ (продолжение)
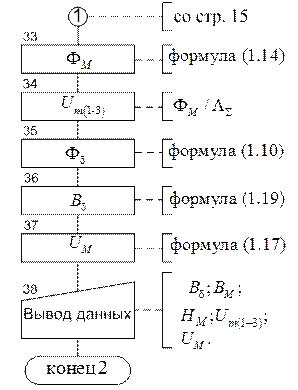
Рис. 1.4. Схема алгоритма анализа ЭМ (окончание)
Задаваясь значением тока I, по алгоритму рис. 1.4 найти соответствующие значения следующих выходных параметров магнитной системы ЭМ:
1) магнитную индукцию в магнитном зазоре ........................ Bd, Тл;
2) координаты, характеризующие положение рабочей точки на основной кривой намагничивания материала магнитопровода ..... НМi, А/м и ВМi, Тл;
3) магнитное напряжение в воздушном зазоре ................. U 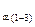 , А;
, А;
4) магнитное напряжение в магнитопроводе ......................... UМ, А.
Расчеты произвести для нескольких значений тока I, указанных преподавателем. Результаты свести в таблицу (форма 1.1).
Форма 1.1
Результаты анализа характеристик ЭМ с помощью его
математической модели
| № п/п | I, А | M, А | Bd, Тл | Hм, А/м | Bм, Тл | Uм(1–3), А | Uм, А |
Эффективность использования материала магнитопровода в некоторой рабочей точке i основной кривой намагничивания можно характеризовать относительной дифференциальной магнитной проницаемостью mri в этой точке, определяемой по формуле
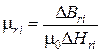 , (1.31)
, (1.31)
где 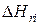 и
и 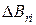 – соответственно приращение координаты H основной кривой намагничивания в i-й точке и соответствующее ему приращение координаты В.
– соответственно приращение координаты H основной кривой намагничивания в i-й точке и соответствующее ему приращение координаты В.
Результаты расчета по формуле (1.31) представлены в виде графиков mr = f(Н) (прил. 1, п. 6).
По данным табл. 1.1 (форма 1.1) построить графики зависимостей:
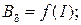 (1.32)
(1.32)
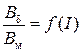 ; (1.33)
; (1.33)
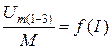 ; (1.34)
; (1.34)
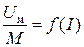 ; (1.35)
; (1.35)
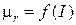 . (1.36)
. (1.36)
ПРИМЕЧАНИЕ. При построении графика зависимости (1.36) использовать связь (табл. 1.1) между напряженностью магнитного поля Н 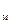 и током I.
и током I.
По результатам анализа сделать вывод.
Дата добавления: 2015-07-22; просмотров: 1315;
