Дифференцирование под знаком интеграла
Вставка
(дифференцирование по параметру)
В предположении существования частной производной 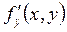 , для вычисления производной
, для вычисления производной 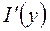 , Лейбниц дал правило, которое в обозначениях Лагранжа записывается как:
, Лейбниц дал правило, которое в обозначениях Лагранжа записывается как:

или, если воспользоваться обозначениями Коши
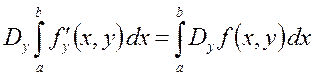
Если такая перестановка под знаком производной допустима, то говорят, что функцию можно дифференцировать по параметру под знаком интеграла. Это вычисление производной под знаком интеграла и получило название правило Лейбница.
Если мы возьмём в (34) функцию 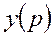 и продифференцируем под интегралом, получим подынтегральную функцию (справа) в (35). Продифференцировав это выражение (под интегралом в (35) - получим подынтегральное выражение в (36). Затем находим вторую производную от левой части (34) . Интегрируя (36) и дважды дифференцируя получим выражение (37).
и продифференцируем под интегралом, получим подынтегральную функцию (справа) в (35). Продифференцировав это выражение (под интегралом в (35) - получим подынтегральное выражение в (36). Затем находим вторую производную от левой части (34) . Интегрируя (36) и дважды дифференцируя получим выражение (37).
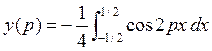 (34)
(34)
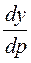 =
= 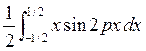 (35)
(35)

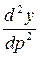 =
= 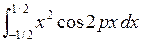 (36)
(36)
В нашем случае 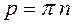 . Интегрируем (34):
. Интегрируем (34):
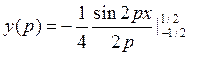 =
= 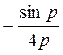 ,
,
более подробно:
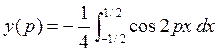 =
= 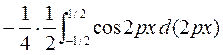 =
= 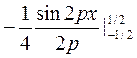 =
=
= 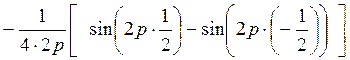 =
= 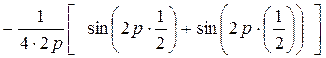 =
=
= 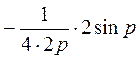 =
= 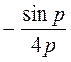 . (37)
. (37)
Дифференцируем (37):
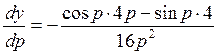 =
= 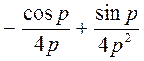 .
.

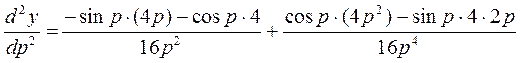 =
=
= 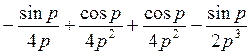 =
= 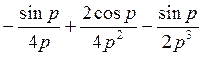 .
.
Подставим 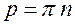

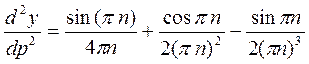 =
= 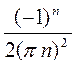 ,
,
т.е. получили, что
 =
= 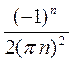 .
.
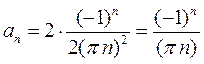 ;
; 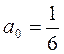 .
.
Найдем 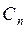
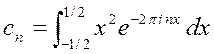 = … или проще
= … или проще 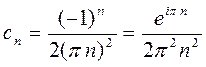 .
.
Откуда имеем:
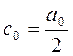
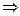
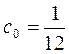 (
( 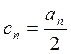 )
)
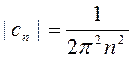 ,
, 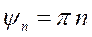 ,
, 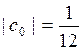 ,
, 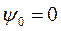 , |
, | 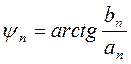 |
|
Нужно обратить внимание, что появилась постоянная составляющая 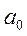 , т.е. площадь под кривой
, т.е. площадь под кривой 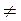 0.
0.
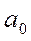 - площадь под кривой!
- площадь под кривой!
По сравнению с «пилой» более быстрое спадание гармоник ( 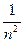 )
)
n = 1 1
n = 2 1/4 = 0.25
n = 3 1/9 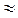 0.11
0.11
n = 4 1/16 = 0.08 ,
т.е. уже не 10 гармоник хватит, а 4. Это связано с большей гладкостью кривой. У функции имеем разрыв производной.
Общее свойство. Чем глаже кривая, тем скорее спадает спектр.
Проверим влияние гладкости кривой на поведение спектра. Рассмотрим функцию f(t) следующего вида, заданную на таком же интервале 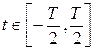 :
:
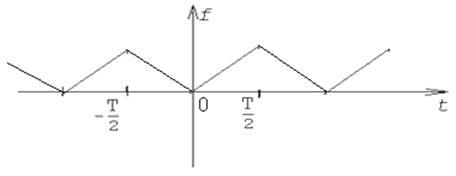 |
Функция – четная, поэтому раскладываем по косинусам
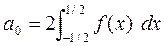 =
= 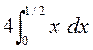 =
= 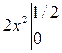 =
= 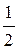 .
.
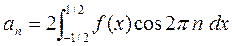 =
= 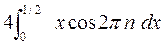 =
= 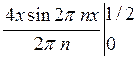 -
-
- 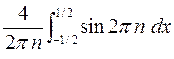 =
= 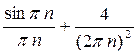 =
=  =
= 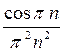 =
= 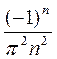 . Т.е. получили, что
. Т.е. получили, что
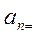
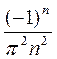
Мы видим, что, по сравнению с предыдущим случаем, меняется только 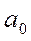 , действительно, площадь изменилась, а спектральные гармоники не меняются.
, действительно, площадь изменилась, а спектральные гармоники не меняются.
В то же время, по сравнению с «пилой», существенное изменение
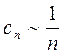 - разрыв f(t)
- разрыв f(t)
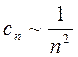 - разрыв f’(t)
- разрыв f’(t)
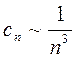 - разрыв f’’(t) , и т.д.
- разрыв f’’(t) , и т.д.
| <== предыдущая лекция | | | следующая лекция ==> |
| НЕКОТОРЫЕ ПАРАМЕТАБОЛИЧЕСКИЕ ПРОЦЕССЫ | | | ПОДГОТОВКА ГОРНЫХ ПОРОД К ВЫЕМКЕ |
Дата добавления: 2015-07-22; просмотров: 1303;
