ТЕМА 2.I МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Методы решения систем линейных алгебраических уравнений разделяются на точные и итерационные. Точные методы представляют собой конечные алгоритмы для вычисления корней системы. Это - метод обратной матрицы, метод Крамера, метод Гаусса, метод Жордана-Гаусса, метод главных элементов, метод квадратных корней и др. Несмотря на то, что методы называются точными, результаты вычислений имеют погрешности вследствие неизбежных округлений при выполнении действий.

Итерационные методы позволяют получать корни системы с заданной точностью путем сходящихся бесконечных процессов. К их числу относятся: метод простой итерации, метод Зейделя, метод релаксации и др. Эффективность применения итерационных методов существенно зависят от удачного выбора начального приближения и быстроты сходимости процесса.

Все вышеперечисленные методы (точные и приближенные) имеют свои преимущества и недостатки и поэтому для выбора оптимального (лучшего) метода для решения конкретной системы линейных уравнений требуются знания пользователя.

А. Пусть дана система n линейных уравнений с n неизвестными

Запишем эту систему в матричном виде

х =

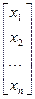или в общем матричном виде

А∙Х=В,

где: А - матрица коэффициентов;

Х – вектор искомых параметров;

В – вектор свободных членов.

Рассмотрим решение линейной системы уравнений различными методами.