Метод Гаусса
Рассмотрим на простейшем примере известный со школы способ исключения неизвестных при решении систем уравнений. Пусть дана система:
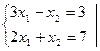

Умножим первое уравнение на такой коэффициент 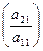 , чтобы в обоих уравнениях коэффициент при х1 стал бы одинаковым
, чтобы в обоих уравнениях коэффициент при х1 стал бы одинаковым
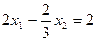
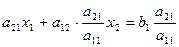
Теперь вычтем его из второго уравнения, т.е.
-2х1+х2=7
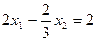
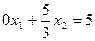
Мы выполнили операцию исключения неизвестной х1 из второго уравнения. Запишем систему уравнения после этого исключения в следующем виде. Первое уравнение записываем в исходном виде.
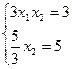
Второе уравнение содержит лишь одно неизвестное, которое легко вычисляется х2=3. Подставив полученное значение х2 в первое уравнение, можем вычислить и первое неизвестное х1.
Проведенные действия и составляют сущность метода Гаусса. Рассмотрим преобразования по методу Гаусса для системы уравнений n-го порядка.
| а11х1+ а12х2+ … +а1nхn=b1 |
| 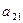
| 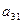
| 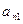
| |||
| а21х1+ а22х2+ … +а2nхn=b2 | 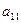
| 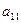
| 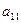
| ||||
| а31х1+ а32х2+ … +а3nхn=b3 | |||||||
| … … … … | |||||||
| аn1х1+ аn2х2+ … +аnnхn=bn |
Вычтем из второго уравнения первое, умноженное на 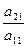 .
.
При этом во втором уравнении будет уничтожен коэффициент при х1.
Затем из третьего уравнения также вычтем первое, умноженное на  .
.
Проделав аналогичные преобразования с остальными уравнениями системы, превратим в нуль все коэффициенты первого столбца, кроме элемента а11. Получим следующую систему:
| а11х1+ а12х2+ а13х3+… +а1nхn=b1 | 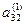
| … | 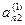
|
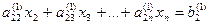
| 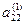
| 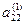
| |
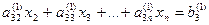
| |||
| … … … … | |||
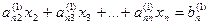
|
Затем при помощи второго уравнения преображенной системы исключим из третьего, четвертого и т.д. уравнений коэффициенты второго столбца лежащие ниже 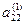
а11х1+ а12х2+ а13х3+… +а1nхn=b1
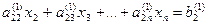
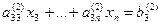
… … …

Последовательно продолжая этот процесс, исключим из системы все коэффициенты, лежащие ниже главной диагонали. В результате получим треугольную систему уравнений.
а11х1+ а12х2+ а13х3+… +а1nхn=b1
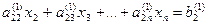
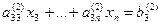
… … …
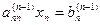
Процесс получения треугольной системы называется “прямым ходом” по методу Гаусса. Треугольная система легко решается “обратным ходом”. Из последнего уравнения определяется последнее неизвестное 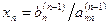 . Затем из предпоследнего уравнения постановкой найденного значения хn определяется хn-1. После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных хi (i= 1, …, n).
. Затем из предпоследнего уравнения постановкой найденного значения хn определяется хn-1. После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных хi (i= 1, …, n).
При решении системы линейных уравнений методом Гаусса все вычисления можно поместить в следующую таблицу. Рассмотрим таблицу на примере решения системы уравнений третьего порядка.
| № шага преобразований | х х1 | х х2 | х х3 | ||
| 1) |  а11 а11
| а12 | а13 | b1 |  : а11 : а11
|
| а21 | а22 | а23 | b2 | ||
| а31 | а32 | а33 | b3 | ||
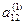
| 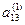
| 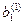
| |||
| 1 2) |  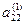
| 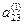
| 
| 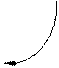 : : 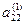
| |
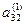
| 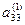
| 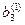
| |||
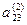
| 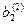
| ||||
| 2 3) | 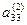
| 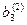
|  : : 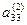
| ||
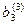
|
Уравнения 1), 2) и 3) составляют искомую треугольную матрицу после “прямого хода”. Число шагов преобразований в “прямом ходе” методом Гаусса равно n-1.
Коэффициенты а11, 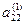 ,
, 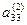 - называются “ведущими” элементами.
- называются “ведущими” элементами.
При “обратном ходе” можно использовать строки таблицы, содержащие единицы, т.е. вспомогательные уравнения. Имеем 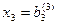 далее
далее
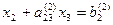
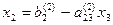
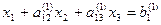
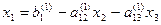
ПРИМЕР:
| № шага | х1 | х2 | х3 | B | ||
| : 4 | ||||||
| 0,25 | 0,5 | х 2 | х 1 | |||
| 7,5 | ||||||
| 1,75 | 3,5 | |||||
| 0,4 | 3,2 | х 1,75 | ||||
| 2,8 | 8,4 | |||||
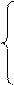 Треугольная система
Треугольная система
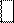 4 х1+х2+2х3=12
4 х1+х2+2х3=12
 7,5 х2+3х3=24
7,5 х2+3х3=24
 2,8 х3=8,4
2,8 х3=8,4
или
 х1+0,25х2+0,5х3=3
х1+0,25х2+0,5х3=3
х2+0,4х3=3,2
х3=3
Обратный ход
х2=3,2-0,4∙3=2
х1=3-0,25∙2-0,5∙3=1
Вычисление определителя методом Гаусса
(третий способ, без вывода)
Определитель матицы А равен произведению всех “ведущих” элементов при преобразовании ее по методу Гаусса.
Для вычисления определителя матрицы А выполняется только “прямой” ход методом Гаусса, причем столбец свободных членов В становится излишним.
ПРИМЕР: дана матрица
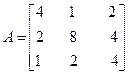 detА=4∙7,5∙2,8=84
detА=4∙7,5∙2,8=84
 Вычисление обратной матрицы методом Гаусса
Вычисление обратной матрицы методом Гаусса
А∙А-1 = Е
Матрицы А и Е известны, требуется определить А-1. Обозначим столбцы матрицы А-1 через х1, х2, …, хn т.е.
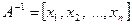
Столбцы для матрицы Е обозначим через Е1, Е2, …, Еn
Тогда можем записать n систем уравнений
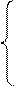 Ах1=Е1
Ах1=Е1
Ах2=Е2
Ахn=Еn
Развернем первое матричное уравнение Ах1=Е1
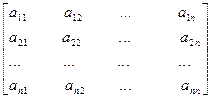 х
х 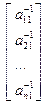 =
= 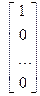
Другие матричные уравнения аналогичны.
Следовательно, для получения обратной матрицы А-1 достаточно выполнить n решений методом Гаусса систем линейных уравнений с разными правыми частями - y столбцами матрицы Е.
Полученные решения х1, х2, …, хn будут столбцами искомой обратной матрицы А-1.
Трангуляции матрицы
Квадратную матрицу А можно представить как произведение двух треугольных матриц А=LW, где
L – нижняя треугольная матрица,
W – верхняя треугольная матрица.
Матрица W вычисляется при прямом ходе Гаусса
а11 а12 а13 … а1n
0 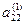
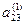 …
… 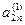
0 0 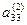 …
… 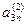
… … … … …
0 0 0 … 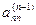
У матрицы L наоборот все элементы выше главной диагонали нулевые. Остальные элементы матрицы L вычисляются в результате деления элементов по столбцам, полученных при том же прямом ходе Гаусса, на ведущие элементы. Сначала вычисляются элементы первого столбца матрицы L делением на ведущий элемент а11, затем после первого шага “прямым ходом” метода Гаусса вычисляются элементы второго столбца, начиная с диагонального, делением на ведущий элемент а11 и т.д.
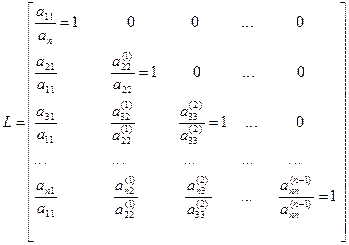
Требуется решить системы уравнений
Ах=В
Так как А=LW то LWх=В
Обозначим Wх=Z
Тогда вместо системы Ах=В можем записать ей эквивалентную
 LZ=В
LZ=В
Wx=Z (5)
Решение эквивалентной системы с треугольными матрицами L и W занимает гораздо меньше времени, чем решение исходной системы Ах=В. Это обстоятельство очень важно при необходимости решать систему уравнений многократно при одной и той же матрице А и разных векторах свободных членов В, что обычно имеет место при расчетах режимов работы электрических систем. Триангуляция же матрицы А проводится только один раз.
 То есть элементы матрицы А – это, как правило, параметры схемы замещения эл. системы, В – вектор узловых токов или мощностей. Часто ставится задача определения параметров большего числа режимов при изменении токов или мощностей потребителей в узлах при неизменной схеме замещения. Если триангуляция матрицы А осуществлена, то можно быстро пользуясь системой (5) посчитать необходимые режимы, меняя в этой системе вектор В. Для каждого режима сначала решается треугольная подсистема LZ=В относительно Z последовательной подстановкой в уравнения подсистемы найденных значений неизвестных из предыдущих уравнений, начиная с Z1
То есть элементы матрицы А – это, как правило, параметры схемы замещения эл. системы, В – вектор узловых токов или мощностей. Часто ставится задача определения параметров большего числа режимов при изменении токов или мощностей потребителей в узлах при неизменной схеме замещения. Если триангуляция матрицы А осуществлена, то можно быстро пользуясь системой (5) посчитать необходимые режимы, меняя в этой системе вектор В. Для каждого режима сначала решается треугольная подсистема LZ=В относительно Z последовательной подстановкой в уравнения подсистемы найденных значений неизвестных из предыдущих уравнений, начиная с Z1
Z1 =b1
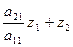 =b2
=b2
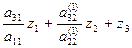 =b3
=b3
… … … … …
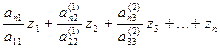 =bn
=bn
Значение Z1 уже известно из первого уравнения, Z2 определяется из второго уравнения подстановкой в него значения Z1 и т.д. Определяются все Z. Затем аналогично решается вторая треугольная подсистема Wx=Z путем обратной подстановки, начиная с хn (аналогично обратному ходу методом Гаусса).
Метод Жордана-Гаусса
Метод Жордана-Гаусса называют еще методом Гаусса без обратного хода. Сущность его состоит в том, что на втором шаге переменная исключается из всех уравнений, кроме второго, на третьем шаге исключается также из всех уравнений, кроме третьего и т.д. После шагов в каждом уравнении остается одна неизвестная, т.е. получим решение системы таким образом, исключение переменных по методу Жордана-Гаусса эквивалентно преобразованию матрицы коэффициентов в единичную. Рассмотрим таблицу вычислений по методу Жордана-Гауса.
| № шага преобразований | A | C | B | ||
| а11 | a12 | … | a1n | b1 | |
| а21 | a22 | … | a2n | b2 | |
| а31 | a32 | … | a3n | b3 | |
| … | … | … | … | … | |
| аn1 | an2 | … | ann | bn | |
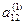
| … | 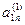
| 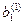
| ||
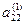
| … | 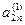
| 
| ||
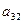
| … | 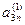
| 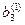
| ||
| … | … | … | … | … | |
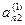
| … | 
| 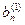
| ||
| … | … | … | … | … | … |
| n | … | 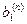
| |||
| … | 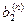
| ||||
| .. | .. | … | … | ||
| … | 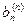
|
Нахождение обратной матрицы методом Жордана-Гаусса
 Рассмотрим вычислительную процедуру определителя А-1 на конкретном примере.
Рассмотрим вычислительную процедуру определителя А-1 на конкретном примере.
А∙А-1=Е
Пусть
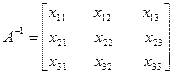
А х1 х2 х3 Е1 Е2 Е3
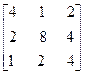 х
х 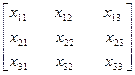 =
= 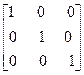
| № шага преобразования | х х1 | х х2 | х х3 | Е1 | Е2 | Е3 |
| 0,25 | 0,5 | 0,25 | ||||
| 7,5 | -0,5 | |||||
| 1,75 | 3,5 | -0,25 | ||||
| 0,4 | 0,2667 | -0,0333 | ||||
| 0,4 | -0,0667 | 0,1333 | ||||
| 2,8 | -0,1333 | -0,2333 | ||||
| 0,2857 | -0,1428 | |||||
| -0,0477 | 0,1666 | -0,1428 | ||||
| -0,0476 | -0,0833 | 0,357 |
Проверка:
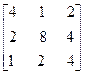 х
х 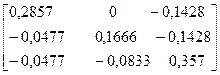 =
= 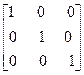
По такой же вычислительной схеме можно вычислять значения переменных х1, х2, х3, …, х при одной матрице коэффициента А и разных столбцах свободных членов В1, В2, В3, …, Вn.
Недостатки метода Гаусса (его недостатки и способы их устранения)
1. Если определитель матрицы А мал, то из-за ошибок округлений сильно снижается точность получения искомых корней.
2. Метод Гаусса требует, чтобы диагональные элементы в процессе исключения переменных не были равны нулю (т.к. строки делятся на них). Поэтому часть применяют метод Гаусса с выбором главного элемента, который заключается в следующем. При обращении в нуль элементов первого столбца из всей матрицы выбирается наибольший элемент и затем в нуль элементы второго столбца, рассматривается сокращенная матрица (путем вычеркивания в уже полученной системе первого уравнения) и в ней наибольший элемент переставляется на ее первое место и т.д.
3. Метод Гаусса требует большего объема памяти ЭВМ по сравнению с итерационными методами. Существуют различные приемы по сокращению занимаемой памяти ЭВМ при решении методом Гаусса электроэнергетических задач.
Например, необходимо решить систему
Yy ∙Uy=Iy
при использовании метода узловых напряжений.

Перенумерация
- Экономичность памяти
- Сокращение времени счета
| Y= | → | |||||||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | ||||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | |||||||||||||||||||||
| + | + | + | + | + | + | + | + | |||||||||||||||||
| + | + | + | + | + | + | + | ||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | + | + | + | |||||||||||||||||
| + | + | + | + | + |
(30 х 70)
Я=10 х 10=100 Я=52 (26)
В ряде случаев для нахождения корней системы линейных уравнений удобнее пользоваться приближенными итерационными методами (или методами последовательных приближений).
Дата добавления: 2015-07-06; просмотров: 2309;
