Сходимости итерационного процесса
Итерационный процесс будет сходящимся, если модуль коэффициента на главной диагонали больше суммы (или равен сумме) модулей остальных элементов строки (свободные члены при этом не учитываются)
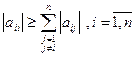
Это достаточное условие сходимости, но не необходимое, т.е. данное условие гарантирует сходимость итерационного процесса. Условие не является чрезмерным в электрических системах оно часто выполняется, в том числе для матриц узловых проводимостей Yу при решении систем узловых уравнений YiUу=Iу и контурных сопротивлений Zк при решении системы контурных уравнений ZкIк= .
Итерационный процесс сходится значительно быстрее, если диагональные элементы матрицы А значительно больше недиагональных элементов. Этого можно добиться меняя строки и столбцы местами, при этом оставляя систему линейных уравнений неизменной относительно значений корней.
Пример:  Условие сходимости не выполняется
Условие сходимости не выполняется
Поменяем строки местами
|
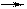

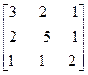 , т.е.
, т.е. 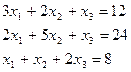
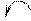
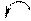 Или поменяем столбцы местами
Или поменяем столбцы местами
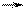

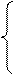
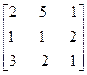
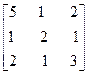 , т.е.
, т.е. 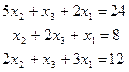
Условие сходимости также выполняется.
Метод итерации обладает таким важным свойством, как самоисправление арифметических ошибок. Можно доказать, что если вычислительный процесс сходится при х(0), то он будет сходится и при другом приближении, которое вычислено с ошибкой. При ошибке у нас только изменится число итераций.
Дата добавления: 2015-07-06; просмотров: 733;
