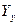Метод узловых напряжений для расчета токораспределения
В этом методе токи в ветвях определяются через разность напряжений в узлах. Число узлов в схемах обычно меньше числа ветвей, поэтому порядок решаемой системы будет меньше, чем при определении токов “прямым” способом.

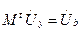
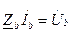
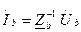

 (1)
(1)
|
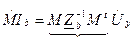

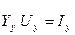 - система узловых уравнений (2)
- система узловых уравнений (2)
Обратная матрица 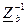
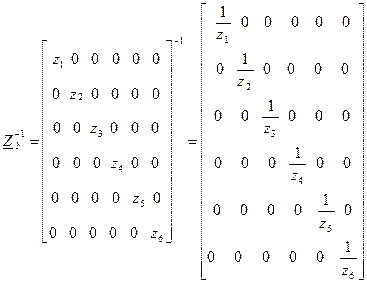
Мt – транспонированная матрица М в случае, когда базисный узел системы совпадает с балансирующим.
Базисный узел – это узел, для которого напряжение задается перед расчетом.
Балансирующий узел – это узел, мощность которого равна алгебраической сумме мощностей всех остальных узлов в системе, т.е. он является балансирующим по мощности (здесь проявляется закон единства производства и потребления электроэнергии, сколько выработано, столько и должно быть потреблено).
В случае, если базисный узел не совпадает с балансирующим, то вместо Мt в формуле (1) ставится 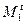 , которая может быть получена из избыточной первой матрицы инциденций М, т.е. содержащей строку для балансирующего узла, путем вычеркивания строки, отвечающей базисному узлу.
, которая может быть получена из избыточной первой матрицы инциденций М, т.е. содержащей строку для балансирующего узла, путем вычеркивания строки, отвечающей базисному узлу.
Для определения падений напряжений в ветвях необходимо решить систему узловых уравнений
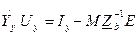 при наличии ЭДС в ветвях
при наличии ЭДС в ветвях
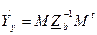 - матрица узловых проводимостей, может быть определена без расчетов непосредственно из схемы
- матрица узловых проводимостей, может быть определена без расчетов непосредственно из схемы
| Yу= | у з л ы | 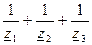
| 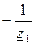
| 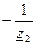
|  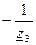
| 
| |
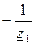
| 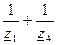
|  
| |||||
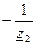
| 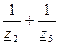
|  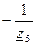
| |||||
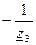
|  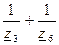
| ||||||

| 4 х 4 |
Элементы из главной диагонали равна сумме проводимостей ветвей, подходящих к соответствующему узлу, а недиагональные элементы равны проводимостям ветвей между соответствующими узлами со знаком минус (-).
Матрица Yу – симметричная.
Итак, по методу узловых напряжений, вначале составляется и решается система уравнений (2) относительно узловых напряжений Uу, затем найденные значения Uу подставляются в выражение (1) и вычисляются искомые токи в ветвях.
2.6. Метод контурных токов [Л-4, с.25-228]
Введем новые переменные – контурные токи II и III.
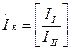 - вектор-столбец контурных токов.
- вектор-столбец контурных токов.
Через контурные токи определяются токи в ветвях
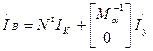 (3)
(3)
Мα – первая матрица инциденций, составленная для дерева схемы (дерево выделено на схеме).
Обратная матрица Мα может быть легко определена по схеме (без процедуры обращения матрицы Мα). Столбцы матрицы 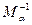 содержат пути по ветвям дерева от каждого узла к балансирующему. Если направление движения от узла к балансирующему не совпадает с выбранным направлением в ветви, то ставится +1, иначе -1. Можно говорить наоборот – от балансирующего к каждому, тогда если направление движения совпадает, то +1 иначе -1.
содержат пути по ветвям дерева от каждого узла к балансирующему. Если направление движения от узла к балансирующему не совпадает с выбранным направлением в ветви, то ставится +1, иначе -1. Можно говорить наоборот – от балансирующего к каждому, тогда если направление движения совпадает, то +1 иначе -1.
| Мα= | у з л ы | ветви | Мα= | в е т в и | Узлы | ||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 |
Можно проверить 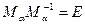
Матрица контурных сопротивлений Zк также может легко определена по схеме. Матрица Zк – квадратная, порядок равен числу контуров. Диагональные элементы равны суммам сопротивлений ветвей входящих в соответствующие контуры, а подиагональные элементы равны сопротивлениям ветвей, общих для двух соседних контуров. Матрица Zк – симметричная, недиагональные элементы берутся со знаком “-”.
 = =
| I | z1+z2+z4+z5 | -z1-z4 |
| II | -z1-z4 | z1+z2+z4+z6 |
Итак, по методу контурных токов сначала составляется и решается система уравнений относительно контурных токов Iк, порядок равен количеству независимых контуров.
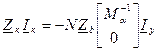 (4)
(4)
Найденные значения контурных токов Iк подставляются в выражение (3) и вычисляются искомые токи в ветвях Ib.
Целесообразность применения метода узловых напряжений или метода контурных токов определяется в зависимости от физических условий задачи, от принятых допущений, которые сейчас мы не рассматриваем. В одних случаях удобен первый метод, в других – второй. Наибольшее же распространение получил метод узловых напряжений, он реализован в большинстве промышленных программ для расчетов режимов электрических систем.
Отметим также следующее.
Элементами ряда матриц в наших задачах являются комплексные числа (а+jb) или (а-jb), что значительно увеличивает расчеты. Основное расчетное время идет на решение систем уравнений (2) и (4). Если уравнения линейны, то они решаются проще известными методами. На самом деле процессы, происходящие в электрической системе имеют нелинейный характер. Приведение уравнений к линейному виду является упрощением задач и используется, когда не требуется точного решения задач.
Далее в разделе 2 мы познакомимся с наиболее известными в широком применении методами решения систем линейных и нелинейных уравнений.
Инженерные методы узловых напряжений (УН) и контурных токов (КТ) позволяют сформировать уравнения (модель) состояния электрической системы, которые затем решаются известными в математике численными методами. Вообще решение многих задач заключается в формировании систем уравнений и вычислении их корней. Поэтому инженеру необходимо знать и уметь применять численные методы решения систем уравнений.
Раздел 2. МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Дата добавления: 2015-07-06; просмотров: 977;