Второй способ вычисления определителя

Определитель матрицы любого порядка равен сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения:

по i-й строке 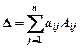i =1, 2, …, n

по j-му столбцу 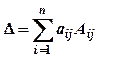j =1, 2, …, n

Пример:

Дана матрица 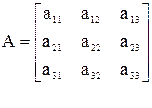. Надо вычислить Δ.

По строке:

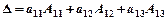
или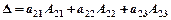

или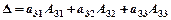

По столбцу:

или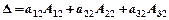

или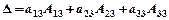

Обычно для вычисления Δ по 2-му способу выбирается строка или столбец, которые содержат больше нулевых элементов, чтобы уменьшить число слагаемых произведений. Согласно схеме вычислений определителя матрицы n-го порядка по 2-му способу необходимо найти определители для матрицы (n-1)-го порядка. Очевидно, что для их нахождения в свою очередь можно использовать ту же схему вычислений и перейти к нахождению определителей матрицы (n-2)-го порядка. И так далее до тех пор, пока не дойдет до матрицы 3-го или 2-го порядка, для которых мы уже умеем вычислять определители.