Определитель

Определитель (или детерминант) является важной числовой характеристикой квадратной матрицы, обозначается через 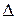или det A и вычисляется по известным правилам. Классический способ вычисления 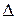(первый способ)

,

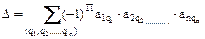где q₁,q₂,…,q_n – произвольная перестановка вторых индексов;

П – число беспорядков в перестановке вторых индексов.

Число слагаемых произведений равно числу возможных перестановок вторых индексов, т.е. равно n!, где n - порядок квадратной матрицы.

Пример:

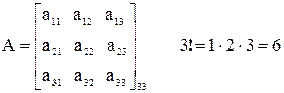
	Возможные перестановки вторых индексов	Число беспорядков
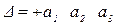
	1) 1 2 3	П=0
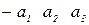
	2) 1 3 2	П=1
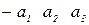
	3) 2 1 3	П=1
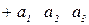
	4) 2 3 1	П=2
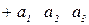
	5) 3 1 2	П=2
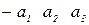
	6) 3 2 1	П=3

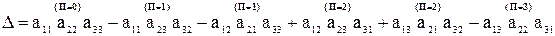
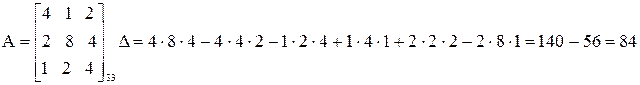
Число слагаемых произведений при вычислении Δ возрастает стремительно с увеличением n:

n = 2 2! = 2

n = 3 3! = 6

n = 4 4! = 24

n = 5 5! = 120

n = 6 6! = 720

Вычислять Δ классическим способом сложно и поэтому применяют другие способы.

Вычисление Δ для матрицы второго порядка (n = 2).

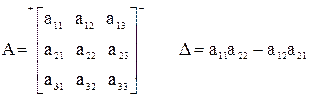
Два частных способа вычисления Δ для матриц только третьего порядка (n = 3).

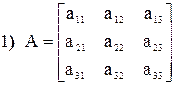
	Слагаемые произведения со знаком +
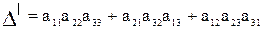
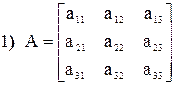
	Слагаемые произведения со знаком -

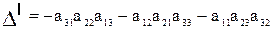
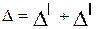
2)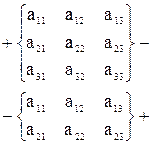

Указанные схемы вычисления Δ для матриц второго и третьего порядков основаны на использовании геометрического расположения элементов в матрицах, что неприменимо для матриц более высокого порядка.