Тема 1.1. Некоторые сведения из теории матричной алгебры
Применение матричной алгебры и теории графов
В электроэнергетике
Тема 1.1. Некоторые сведения из теории матричной алгебры
Классификация матриц
Система m n чисел, действительных или комплексных, расположенных в прямоугольной таблице из m строк и n столбцов называется матрицей
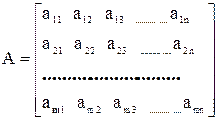 .
.
где aij – элементы матрицы;
i = 1, 2, 3,…., m – номера строк;
m – число строк в матрице;
j = 1, 2, 3,…., n – номера столбцов;
n – число столбцов.
Для матрицы часто используется сокращенная запись 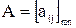 , где m·n – размерность матрицы.
, где m·n – размерность матрицы.
Если m = n (m ≠ 1, n ≠ 1), то матрица называется квадратной.
Если m ≠ n (m ≠ 1, n ≠ 1), то матрица называется прямоугольной.
Если m = n = 1, то матрица - скаляр.
Если m = 1, а n ≠ 1, то матрица называется вектор-строкой
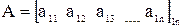 .
.
Если n = 1, а m ≠ 1, то матрица называется вектор-столбцом
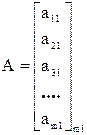 .
.
Матрица нулевого порядка смысла не имеет.
Квадратная матрица, у которой диагональные элементы не равны нулю, а все недиагональные элементы равны нулю, называются диагональной
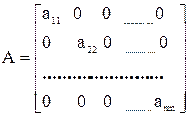
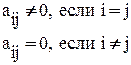
Диагональная матрица, у которой все ненулевые элементы равны единице, называется единичной и обозначается Е
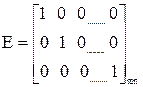 .
.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О
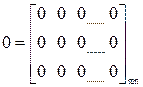 .
.
Дата добавления: 2015-07-06; просмотров: 1003;
