Теории электродной поляризации

Первая теория электродной поляризации была разработана Нернстом в конце XIX - начале XX вв.

В соответствии с теорией Нернста электродный потенциал электрода как находящегося в равновесных условиях, так и под током, выражается одним и тем же уравнением. Например, потенциал электрода 1-го рода выражается уравнением:

.

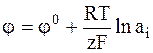Термодинамическую активность иона а_i можно выразить через молярную концентрацию С_i и коэффициент активности f_i:

a_i = f_iC_i

и уравнению для электродного потенциала можно придать следующий вид:

.

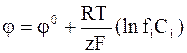Для сравнительно невысоких концентраций коэффициент активности можно принять постоянным и включить 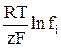вместе со стандартным электродным потенциалом в общую константу:

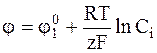. (6 - 9)

Так как для электрода, находящегося в равновесных условиях и под током, используется одно и то же уравнение, то из условий (6 - 7) и (6 - 8) следует, что вблизи поверхности электрода должны также выполняться следующие условия:

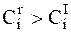для катода; (6 - 10)

для анода, (6 - 11)

где 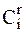- концентрация ионов вблизи электрода при равновесных условиях, 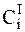- концентрация ионов вблизи электрода, находящегося под током.

Соотношения (6 - 10) и (6 - 11) непосредственно вытекают из основного уравнения электродной поляризации:

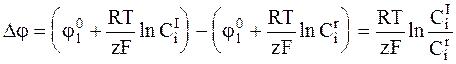. (6 - 12)

Нернст предложил метод расчета концентрации ионов вблизи электрода, находящегося под током ( 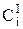). Суть этого метода можно продемонстрировать на примере процессов, протекающих в следующей электрохимической системе:

M½M^z+, A^x−½M.

Если через раствор за время t проходит количество электричества, равное 1 фарадею, то на катоде разряжается 1 моль эквивалентов, а сила тока составит:

.

При числе переноса ионов M^z+, равном t₊, в этих условиях электрический ток доставит к катоду t₊ моль эквивалентов катионов. Скорости разряжения ионов на катоде и их доставки окажутся равными соответственно:

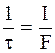- скорость разряжения ионов на катоде;

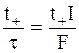- скорость доставки ионов к катоду.

Так как скорость доставки ионов электрическим током меньше скорости, с которой они разряжаются на катоде, то в прикатодном пространстве возникает дефицит катионов. Скорость возрастания дефицита равна .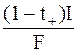

В стационарных условиях дефицитообразование, вызванное различиями скоростей выделения и доставки ионов, должно компенсироваться каким-либо другим процессом. Нернст предположил, что таким процессом является диффузия. В связи с этим его теория получила название диффузионной теории поляризации.

Диффузионный поток ионов определяется законом Фика. В предположении, что в прикатодном пространстве (оно рассматривается как имеющее толщину d порядка молекулярных размеров) концентрация ионов с расстоянием от катода изменяется линейно, а градиент концентрации можно представить следующим образом:

,

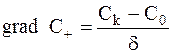где С_k - молярная концентрация катионов вблизи катода, C₀ - молярная концентрация ионов в объеме раствора (вне прикатодного пространства).

Диффузионный поток ионов, коэффициент диффузии которых равен D₊, к катоду, имеющему площадь S, в соответствии с законом Фика равен:

.

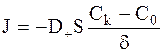Для потока, выражаемого числом моль эквивалентов, определяющих переносимый заряд, можно записать:

.

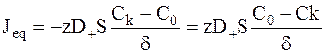Следовательно, для стационарных условий выполняется равенство:

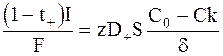. (6 - 13)

Концентрация ионов M^z+ вблизи катода равна:

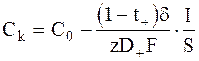. (6 - 14)

Объединив все постоянные, включая число переноса, коэффициент диффузии и толщину приэлектродного слоя, в одну константу k и принимая во внимание, что отношение силы тока к площади электрода представляет собой плотность тока i, получим:

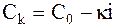. (6 - 15)

С учетом выражения (6 - 15) запишем уравнение для катодной поляризации:

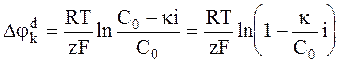. (6 - 16)

В отличие от катодной поляризации анодная поляризация сопровождается избыточным (по сравнению с транспортируемым током) переходом ионов в раствор. В связи с этим диффузионный поток приводит к отводу ионов от анода, то есть имеет противоположное направление. В связи с этим для анодной поляризации должно выполняться уравнение:

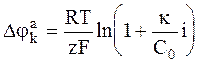. (6 - 17)

Из уравнения (6 - 16) следует, что для катодной поляризации должен существовать предел плотности тока, который равен:

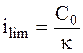. (6 - 18)

С учетом равенства (6 - 18) уравнение для катодной поляризации принимает следующий вид:

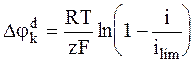. (6 - 19)

Если процесс растворения анода не сопровождается другими явлениями, анодная поляризация не должна иметь предельного тока.

Уравнения (6 - 16) - (6 - 19) позволяют понять, каким образом можно экспериментально изучать поляризацию отдельных электродов. Действительно, если площадь одного из двух электродов во много раз больше площади другого, то на электроде с большей площадью плотность тока будет настолько мала, что поляризацией его можно пренебречь. В этом случае ЭДС поляризации окажется равной поляризации электрода с меньшей площадью.

Явление поляризации лежит в основе важного электрохимического метода анализа - полярографии.

В заключение отметим, что еще одной причиной поляризации электродов может служить замедление присоединения электронов к ионам или отрыва электронов от атомов.