Диффузионный потенциал

Скачок потенциала, вызываемый различиями коэффициентов диффузии ионов и возникающий между двумя растворами, называется диффузионным потенциалом.

Для расчета диффузионного потенциала можно воспользоваться уравнением, получаемым интегрированием уравнения (5 ‑ 14). Действительно, из уравнения (5 - 14) следует для одномерного движения частиц (движения вдоль одного координатного направления):

;

;

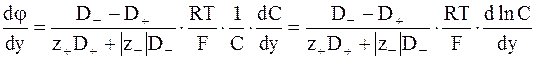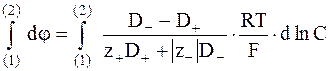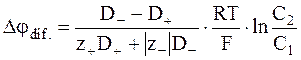. (5 - 19)

Кроме уравнения (5 - 19), для расчета диффузионного потенциала на границе двух растворов можно воспользоваться уравнением, в котором вместо коэффициента диффузии отдельных ионов используются их абсолютные подвижности. Такое уравнение можно получить, используя равенства типа (5 - 11):

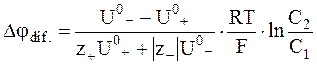. (5 - 20)

Для достаточно концентрированного бинарного электролита вместо концентрации используется активность электролита:

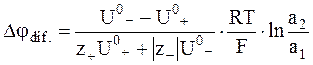. (5 - 21)

Уравнение (5 - 21) является частным случаем более общего уравнения, полученного М. Планком.

Планк разработал квазитермодинамическую теорию диффузионного потенциала.

Основная идея этой теории заключается в предположении, что пространственное разделение зарядов в результате неодинаковой диффузии ионов сопровождается электрической работой.

Если между граничащими растворами взять предельно узкую часть пространства, ограниченную двумя плоскостями, то ей должна соответствовать разность потенциалов, равная dj. Выбрав такую границу, чтобы через плоскости проходил заряд, равный постоянной Фарадея F, найдем, что электрическая работа равна

.

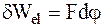В предположении, что разделение зарядов в диффузионном процессе происходит квазистатически (это предположение не соответствует полностью термодинамическим представлениям о квазистатическом процессе и по этой причине теория называется квазитермодинамической), можно принять, что при постоянных Р и Т работа происходит за счет убыли энергии Гиббса:

dW_el = −dG.

Если при переходе от одной плоскости к другой термодинамическая активность i-го вещества изменяется на da_i, то перенос одного моля этого вещества приводит к изменению энергии Гиббса на величину, равную

dG_i⁽¹⁾ = RTdlna_i.

Перенос n_i молей этого вещества приводит к изменению энергии Гиббса на следующую величину:

dG_i = n_iRTdlna_i.

Перенос всех веществ через эти плоскости приводит к полному изменению энергии Гиббса:

.

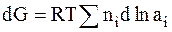Таким образом, скачок потенциала между выбранными плоскостями окажется равным

,

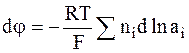а скачок потенциала между двумя растворами, то есть на протяжении всей границы, можно получить как результат интегрирования:

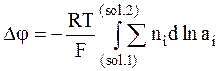. (5 - 22)

Заряд, переносимый данным сортом ионов i, при условии, что заряд одного иона в а.е.з. равен z_i, а число моль ионов равно n_i, будет выражен z_in_i.

Введем новое понятие – число переноса, которое представляет собой переносимую данным сортом ионов долю общего заряда, проходящего по цепи.

В соответствии с этим определением число переноса t_i может быть выражено равенством

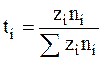. (5 - 23)

Так как было условлено, что суммарный заряд, переносимый по цепи, равен постоянной Фарадея, то в этом случае Sz_in_i = 1, t_i =z_in_i и n_i =t_i/z_i. Следовательно, уравнению (5 - 22) можно придать следующий вид:

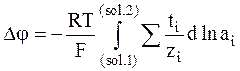. (5 - 24)

Для бинарного электролита число переноса равно отношению абсолютной подвижности данного сорта ионов к сумме абсолютных подвижностей обоих сортов ионов и мы вновь приходим к уравнению (5 - 21).

Экспериментальные данные показывают, что диффузионный потенциал может достигать нескольких десятков милливольт. Таким образом, при расчете стандартных электродных потенциалов может вкрасться серьезная ошибка.

Уравнение (5 - 21) позволяет понять, каким образом можно устранить влияние диффузионного потенциала.

Диффузионный потенциал окажется минимальным, если растворы соединяют солевым мостиком, содержащим концентрированный раствор электролита, образующего ионы с близкими абсолютными подвижностями.