Понятие множества

Понятие множества является фундаментальным неопределяемым понятием.

Интуитивное определение множества – множество есть совокупность определенных и различных объектов (элементов).

Ведем некоторые соглашения об обозначениях элементов теории множеств и логики.

Множество мы будем задавать явным перечислением, и заключать в фигурные скобки. Например: D - множество дней недели: D = {Пн, Вт, Ср, Чт, Пт, Сб, Вс}, D₁ = {Вт, Ср, Чт, Пн, Сб, Пт, Вс}. D и D₁ эквивалентны, т.е. порядок элементов не важен.

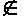Будем использовать обозначения: x A - x есть элемент, и принадлежит множеству A; x A - x не является элементом множества А.

Для бесконечных множеств метод перечисления элементов множества не применим, для этого используется характеристическое свойство А = {x | p(x)}, где х – переменная, значениями которой являются некоторые объекты, а р – свойство тех и только тех значений х, которые являются элементами задаваемого множества.

Пустое множество - множество, которое не содержит ни одного элемента, обозначается Ø или { }.

Если каждый элемент множества А является элементом множества В, то множество А является подмножеством множества В, будем писать A 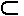B.

Если хотя бы один элемент множества А не является элементом множества В, то множество Ане является подмножеством множества Ви это записывается А В.

Два множества А и В считают равными, если они состоят из одних и тех же элементов. Запись А = В, а А 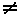В означает неравенство множеств.