ИЗМЕРЕНИЕ ИНВЕСТИЦИОННЫХ РИСКОВ
Риск — это феномен, который проявляется в обстоятельствах, ког-
да представляется реальным идентифицировать возможные исходы
и вероятность их осуществления, не будучи уверенным, какой имен-
но исход будет иметь место в действительности. Неопределенность
характерна для ситуации, когда оценка вероятностей не представля-
ется возможной.
Так как не существует адекватных инструментов, которые могли
бы использоваться для принятия решения в случае неопределенно-
сти. необходимо:
—пытаться идентифицировать как можно большее число воз-
можных вариантов реализации инвестиционного проекта;
—стремиться оценить вероятность появления каждого исхода.
При оценке эффективности инвестиционного проекта с учетом
фактора неопределенности каждый его параметр рассчитывается как
случайная величина. Случайная величина характеризуется матема-
тическим ожиданием (ожидаемая величина дохода, чистого дискон-
тированного дохода и т.д.) и средним квадратическим отклонением
(степень отклонения случайной величины от ожидаемого значения).
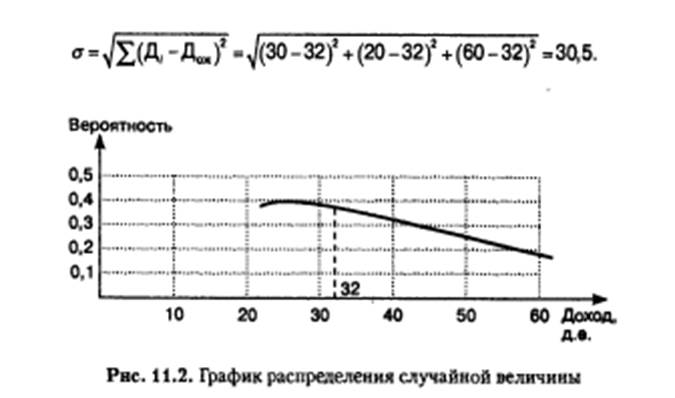
Пример 11.1. По мнению экспертов, вероятность получить доход
по проекту 30 д.е. составляет 40%, 20 д. е. — 40%, 60 д. е. — 20%
(рис. 11.2).
Ожидаемая величина дохода составит:
Дож. = ∑Дi ×Pi = 30 ×0.4 + 20 × 0.4 + 60 ×0,2 =32 д.е.
Так как инвестиционный риск характеризует вероятность возник-
новения непредваденных финансовых потерь, его уровень определя-
ется как отклонение ожидаемых доходов от средней или расчет-
ной величины. Поэтому оценка инвестиционных рисков всегда связана
с оценкой ожидаемых доходов и вероятности их потерь.
При оценке возможного размера финансовых потерь используются
абсолютные и относительные показатели. Абсолютный размер
финансовых потерь представляет собой сумму убытка (ущерба), при-
чиненного инвестору (или потенциально возможного) в связи с на-
ступлением неблагоприятного обстоятельства, характерного для
данного риска. Относительный размер финансовых потерь пред-
ставляет собой отношение суммы убытка (ущерба) к избранному ба-
зовому показателю (например, к сумме ожидаемого дохода от инве-
стиций, к сумме инвестируемого капитала и др.).
Чтобы количественно определить величину риска, необходимо
знать все возможные последствия какого-либо действия и вероят-
ность каждого из этих последствий.
Вероятность означает возможность получения определенно-
го результата:
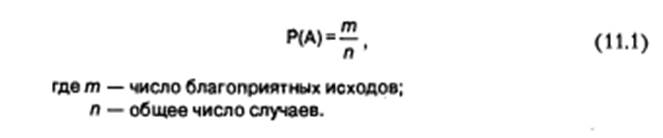
Вероятность наступления события может быть определена тремя способами.
1. Объективный (статистический) базируется на анализе подобных ситуаций в прошлом. Он основан на вычислении частоты наступления событий. Изучается статистика имевших место потерь и прибылей, полученных в результате осуществления аналогичных проектов, устанавливаются величина и частотность получения некоторого показателя и на этой основе составляется прогноз на будущее. Требует значительного массива данных.
2.Субъективный (экспертный) — представляет собой мнение экспертов. Применяется при отсутствии большого количества данных, базируется нв использовании субъективных критериев. Субъективная вероятность является предположением относительно определенного результата. Это предположение основывается на суждении или личном опыте оценивающего (эксперта, консультанта и т.п.).
3.Комбинированный способ.
Как субъективная, так и объективная вероятность используются при определении показателей, которыми можно измерить степень риска.
Методы измерения инвестиционных рисков
1. Расчет среднеквадратического отклонения.
Смысл метода заключается в оценке степени отклонения потока денежных средств для данного инвестиционного проекта от ожидаемого.
Чем больше отклонение, тем более рискованным считается проект.
Пример 11.3. Допустим, мы рассматриваем два инвестиционных проекта I и II, по которым оценены возможные денежные потоки при разных состояниях экономики (табл. 11.1).
Таблица 11.1
| Денежные потоки инвестиционных проектов |
| Состояние | Денежные потоки, д.е. | |||
| экономики | I | Вероятность | II | Вероятность |
| Глубокий спад | 0,1 | од | ||
| Средний спад | 0,2 | 0,2 | ||
| Нормальное | 0,4 | 0,4 | ||
| Небольшой подъем | 0,2 | 0,2 | ||
| Рост | 0,1 | ОД | ||
| Ожидаемое значение |
Вероятность

Рис.11.3.График дисперсии для результатов с неодинакофой вероятностью.
Таким образом, из рис. 11.3 видно, что отклонение величины денежного потока от наиболее вероятного значения больше по варианту II, т.е. для него больше и риск. Математически это отклонение (разброс, дисперсия) оценивается средним квадратическимотклонением.
Проекты I и II (рис. 11.4) характеризуются примерно одинаковым среднеквадратическим отклонением, т.е. степень риска у них
одинаковая, но величина ожидаемого дохода у проекта II выше
<Дож11 > Дож1), значит, он эффективнее.
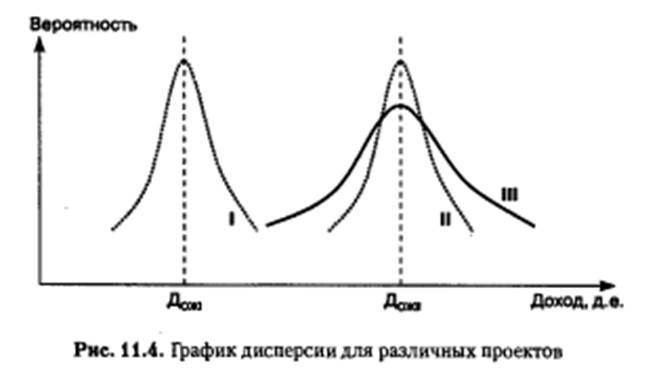
Проекты II и III характеризуются одинаковой величиной ожида-
емого дохода. Однако вероятность его получения у проекта III ниже,
кроме того, он и более рискован, так как величина отклонения от ожи-
даемого дохода у него выше. Поэтому следует выбрать проект II как
менее рискованный, но приводящий к такому же ожидаемому резуль-
тату, что и проект III.
Среднеквадратическое отклонение (Õ) является наиболее рас-
пространенных» показателем оценки уровня инвестиционных рисков.
Расчет этого показателя позволяет учесть возможные колебания ожи-
даемого показателя.
Последовательность расчетов такова.
1.Расчет среднего ожидаемого значения показателя.
Среднее ожидаемое значение - то значение показателя, которое
связано с неопределенной ситуацией. Оно является средневзвешен-
ным всех возможных результатов реализации инвестиционного про-
екта, где вероятность каждого результата используется в качестве веса
соответствующего значения, т.е. это как бы средневзвешенное значе-
ние всех возможных результатов:
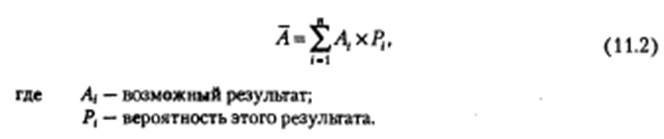
2. Расчет показателя вариации (разброса).
Этот показатель меряет дисперсию (разбросанность) значений
всех возможных вариантов реализации инвестиционного проекта вок-
руг величины ожидаемого результата. Чем больше вариация. т*м боль-
ше дисперсия (разбросанность) по сравнению с ожидаемым результа-
том, тем больше риск проекта: -
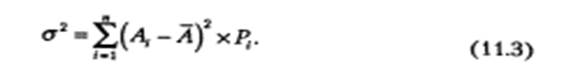
3 Расчет среднего квадратического отклонения (стандартной девиации):
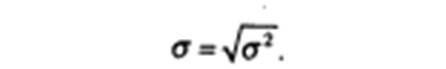
Среднее квадратическое отклонение показывает, на сколько веред-
нем в абсолютном выражении каждый возможный вариант р^лиза-
и"всст"Цио""Ого проекта отклоняется от средней величины. Этот
показатель характеризует абсолютную величину риска. Чем выше
среднее квадратическое отклонение о. тем выше риск
Пример 11.4. Сравнить два инвестиционных проекта по уровню рис-
ка на основе расчета среднеквадратического отклонения. Основные
параметры возможных вариантов реализации проектов приведены
в тэол. 11.2, 11.3.
Таблица 11.2
Распределение вероятностей ожидаемых доходов по вариантам сравниваемых инвестиционных проектов
|
Так как Õ= 288 > Õ1= 134, проект II характеризуется большим уровнем риска.
2. Расчет коэффициента вариации.
Недостатком среднего квадратического отклонения является его абсолютная величина, что делает неудобным сравнение инвестиций с различными значениями ожидаемого результата.
Коэффициент вариации позволяет определить уровень риска, если, средние ожидаемые значения показателей различаются между собой.
Коэффициент вариации (у) — относительный показатель риска, который представляет собой риск на единицу ожидаемого результата:

Пример 11.5. Рассчитаем коэффициент вариации для проектов I и II из примера 11.4.
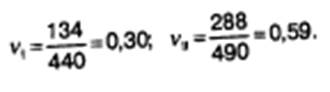

ß-коэффициент (бета-коэффициент)
Для измерения величины систематического риска существует спе-
циальный показатель - р-коэффициент, который позволяет оценить
риск индивидуального инвестиционного проекта по отношению к уров-
ню риска инвестиционного рынка в целом. Этот показатель в основ-
ном используется для анализа рискованности вложений в отдельные
ценные бумаги, ß-коэффнцнент определяет влияние общей ситуации
на рынке на судьбу каждой ценной бумаги с использованием следу-
ющего критерия:
ß=1-средний уровень риска;
ß>1-высокий уровень риска;
ß<1-низкий уровень риска.
3. Экспертный метод
Экспертный метод используется, когда отсутствует информация
или статистические данные для расчетов (например, инвестиционный
проект не имеет аналогов). Этот метод базируется на опросе квалифи-
цированных специалистов и соответствующей математической обра-
ботке результатов этого опроса.
Дата добавления: 2015-07-18; просмотров: 2472;
