Плоские линейные антенны поверхностных волн.

1. Антенны с диэлектрическим направителем. Рассмотрим антенну, изображенную на рис. 14.2. Будем считать, что длина выступающей за пределами направителя части экрана. Пусть относительная диэлектрическая проницаемость направителя равна e_Г.

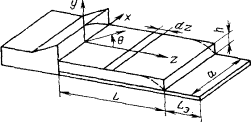
Рис. 14.2. Плоская линейная антенна поверхностных волн.

Волны типа Е, как известно из теории электромагнитного поля [1], могут распространяться вдоль направителя, если в раскрыве возбуждающего рупора электрический вектор параллелен оси у. Если толщина направителя h< 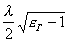, то будет распространяться только волна типа Е₀(рис.14.3, а), не имеющая критической длины волны. Амплитуда поля будет убывать по экспоненциальному закону в направлении оси Oy (рис.14.3, б). Волна типа Ео имеет две составляющие: Еу и Еz. Поверхностная волна будет распространяться вдоль оси Оz с фазовой скоростью v_ф, которая может быть определена из трансцендентного уравнения:

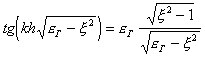,(14.1)

где коэффициент замедления x=с/v_Ф. Если kh>0, то x<1 и v_Ф>c. Если kh растет, то x< 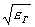и v_Ф=c/ 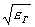. Таким образом, фазовая скорость находится в пределах:c/ 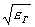>v_{Ф <} с.

Пренебрегая излучением с боковых и торцевой стенок направителя, можно в первом приближении считать, что антенна имеет излучающий раскрыв с размерами L и а. Амплитудно-фазовое распределение в этом раскрыве можно приближенно считать разделяющимся. Вдоль оси Oz фаза изменяется по закону бегущей волны, а амплитуду в первом приближении можно считать неизменной (если потери в диэлектрике и в подложке малы). Вдоль оси Ох распределение поля такое же, как в возбудителе.

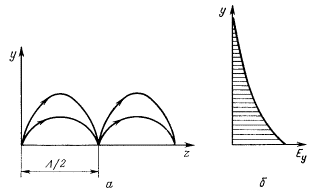
Рис. 14.3. Структура поля волны типа Е₀ (а);

убывание составляющей Еу вдоль координаты у (б).

Из сказанного следует, что ДН антенны в плоскости yOz (Е-плоскости) зависит только от продольного размера L и по теореме умножения диаграмм может быть представлена в виде:

f(q)=fо(q)f_С(q).(14.2)

Здесь fо(q) - ДН элементарного излучателя, в качестве которого можно принять полоску длиной dz (см. рис.14.2). Так как у поверхности направителя касательная составляющая электрического поля ориентирована вдоль оси Oz (перпендикулярно краям полоски), то такую полоску можно рассматривать как прямолинейную щель, для которой в Е-плоскости fo(q)=1 (см. §10.3); f_С(q) - ДН непрерывной прямолинейной равноамплитудной системы осевого излучения. Как было показано ранее (см. §3.4),

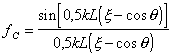,(14.3)

Так как x>1, то главный лепесток ДН ориентирован вдоль оси Oz. ДН имеет вид, типичный для антенн осевого излучения. Для оценки формы ДН можно обратиться к рис.3.12, в котором, однако, из-за бесконечной длины металлического экрана имеет смысл только верхняя половина ДН.

Формула (14.3) получена в предположении, что толщина направителя не меняется по длине антенны, т.е. x=const. В действительности для согласования антенны со свободным пространством ее толщину уменьшают к концу (пунктирные линии на рис.14.2). В этом случае в формулу (14.3) нужно подставлять среднее значение x по длине антенны.

Оптимальная длина антенны (при которой КНД максимален) определяется по формуле (3.63)

L_ОПТ = l/2(x-1).(14.4)

Диаграмма направленности антенны в плоскости хОz (H-плоскости) определяется также по формуле (14.2), в которой под fo(q) следует понимать ДН полоски шириной а и длиной dz, но теперь уже в плоскости Н, т. е. fo(q) есть ДН возбудителя в плоскости Н, так как размер и амплитудно-фазовое распределение вдоль оси Ох у полоски и возбудителя одинаковы.

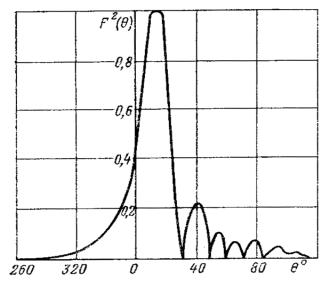
Рис. 14.4. ДН антенны поверхностных волн в плоскости,

перпендикулярной экрану.

У реальных антенн длина экрана не бесконечна. У края экрана происходит дифракция волн, что влияет на форму ДН. Если La=0, то для расчета ДН в освещенном полупространстве формула (14.2) применима, но хорошее совпадение расчетных и экспериментальных ДН получается в том случае, если в формуле (14.2) под fo(q) понимать ДН излучателя Гюйгенса, расположенного в раскрыве антенны. Можно показать [2], что

.(14.5)

Так как максимумы функций fо(q) и fс(q) имеют место соответственно при углах q = 90° н q = 0, то главный лепесток ДН отклонен от экрана на некоторый угол, который тем меньше, чем больше длина антенны и чем больше замедление x. Типичная ДН приведена на рис. 14.4. Некоторое излучение наблюдается и в затененное полупространство (ниже экрана).

Если L = 0, то для определения поля излучения нужно учитывать еще излучение токов, обтекающих выступающую часть экрана, что значительно усложняет расчет [2].

Волны типа Н будут распространяться вдоль направителя в том случае, если электрический вектор поля в раскрыве возбудителя (см. рис.14.2) параллелен оси Ох. Для того чтобы распространялась только основная магнитная волна типа Но, необходимо выполнить условие: .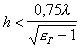

В отличие от волны типа Еo волна типа Нo имеет критическую длину волны, поэтому для того чтобы волна Но могла существовать, необходимо выполнить условие: .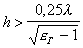

Расчет поля излучения антенны в случае волны типа Но производится так же, как и в случае волны типа Ео. Различие между двумя антеннами состоит в том, что в случае волны типа Но не только при конечной длине экрана, но и при бесконечной его длине главный лепесток отклонен от плоскости экрана. Это объясняется тем, что касательная составляющая электрического вектора в раскрыве антенны параллельна оси Ох (см. рис.14.2), а следовательно, ДН элементарного излучателя в плоскости yOz должна рассчитываться как для элементарной щели в H-плоскости по формуле fо(q)=sinq.

Таким образом, излучения вдоль экрана (при q = 0) нет в случае волны типа Но.

2.Антенны с ребристым направителем. Из теории электромагнитного поля известно [1], что вдоль ребристой структуры могут распространяться поверхностные волны типа Е. Наибольший интерес представляет основная волна типа Ео, структура которой подобна структуре волны типа Ео, распространяющейся над диэлектрическим замедлителем (см. рис.14.3).

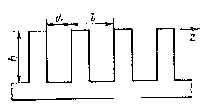
Рис. 14.5. Ребристая структура.

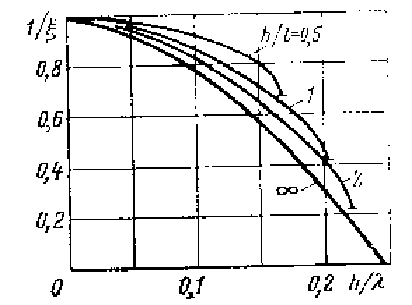
Рис. 14.6. Зависимость обратной величины коэффициента замедления (1/x=v_ф/с) от параметров ребристой структуры.

Условие существования поверхностной волны имеет вид: l<l/2x, где l - период ребристой структуры (рис.14.5). Поверхностная волна типа Ео распространяется в направлении оси z, перпендикулярной ребрам, с фазовой скоростью, которая может быть приближенно определена по формуле:

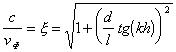,(14.6)

где h и d - соответственно глубина и ширина канавок.

Из формулы (14.6) видно, что с увеличением глубины канавки фазовая скорость убывает и при h=l/4 она равна нулю, что соответствует срыву распространения поверхностной волны. Детальный анализ показывает [1], что отношениеh/l, при котором происходит срыв, зависит от «густоты» структуры, т. е. отношения h/l.

Результаты расчета фазовой скорости волны типа Ео, распространяющейся вдоль ребристой структуры, приведены на рис.14.6. Обрывы кривых соответствуют срыву поверхностной волны.

При известной фазовой скорости расчет направленных свойств ребристых антенн ничем не отличается от расчета антенн с диэлектрическим направителем.