Сигналы непрерывные и дискретные. Преобразование сигналов.

Информация (сообщения и сигналы) может существовать в двух формах: непрерывной и дискретной.

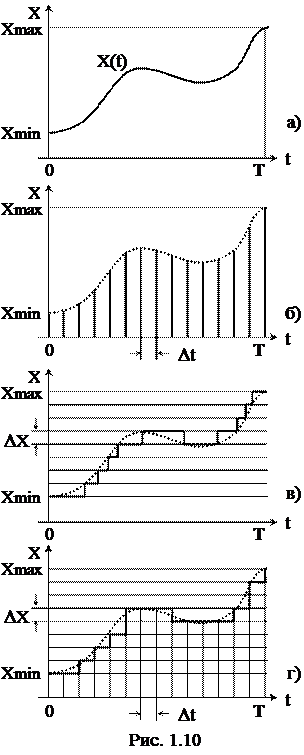
В большинстве случаев информация о протекании того или иного физического процесса вырабатывается соответствующими датчиками в виде сигналов, непрерывно изменяющихся во времени. Такой сигнал можно представить в виде непрерывной функции Х(t) непрерывного аргумента t – функции, которая может принимать любые вещественные значения в интервале (X_min, X_max) для любых значений аргумента t в интервале (0, Т) (рис. 1.10а). Множество значений непрерывной функции бесконечно.

Дискретные сообщения и сигналы состоят из конечного множества элементов, поступающих последовательно во времени. Набор элементов (символов) составляет алфавит источника дискретной информации. Обычно элементами дискретных сигналов являются последовательности чисел.

Для передачи информации по каналу связи и ее дальнейшей обработки средствами вычислительной техники непрерывный сигнал преобразуют в дискретный. Это преобразование осуществляется с помощью специальных устройств – преобразователей непрерывных сигналов и может быть выполнено дискретизацией во времени, квантованием по уровню или одновременно дискретизацией во времени и квантованием по уровню. При этом соответственно возможны три разновидности сигналов.

Дискретизация во времени состоит в преобразовании непрерывного сигнала Х(t) непрерывного аргумента t (рис. 1.10а) в непрерывный сигнал Х(t_i) дискретного аргумента t_i с шагом дискретизации ∆t (рис. 1.10б). Сигнала Х(t_i) может принимать любые значения в интервале (X_min, X_max), но лишь на дискретном множестве значений аргумента t_i (t₁, t₂, …,t_к) в интервале (0, Т). Какой бы малый шаг дискретизации не выбирался, множество значений дискретной функции будет конечно (ограничено). Примером такого сигнала может быть последовательность импульсов, модулированных по амплитуде. Рассмотренная дискретизации является равномерной, т.к. длительность шага дискретизации ∆t_i=const на всем интервале (0, Т). Дискретизация может быть и неравномерной, если длительность шага ∆t_i различна (∆t_i=var). Методы изменения шага ∆t_i могут быть адаптивными, когда он изменяется в зависимости от текущего изменения параметров сигнала, и программируемыми, когда он изменяется в соответствии с заранее установленной программой или оператором, на основе анализа поступающей информации. Очевидно, что каждый вид дискретизации имеет свои преимущества и недостатки. Все же в основном, применяется равномерная дискретизация, так как алгоритмы и аппаратура для ее реализации существенно проще. Однако очевидно, что при этом в случае медленно изменяющихся сигналов возможны «лишние» отсчеты, т.е. избыточность информации.

Квантование по уровню состоит в преобразовании непрерывных значений сигнала Х(t_i) в дискретные значения. При этом образуется дискретный сигнал непрерывного аргумента; соседние значения сигнала различаются на элементарную величину ∆Х – квант (рис. 1.10в). Значения, которые может принимать сигнал Х(t), образуют дискретный ряд заранее заданных чисел Х₁, Х₂,…Х_к или уровней 1, 2, 3, 4 и т.д.; значение аргумента t может быть любым в интервале (0,Т). Примером такого сигнала может быть сигнал на выходе проволочного потенциометра, выходное напряжение которого квантуется за счет скачков сопротивления при перемещении движка с витка на виток. Можно отметить, что квантование по уровню может быть и неравномерным, если ∆Х=var. В основном, используется равномерное квантование - ∆Х=const.

Первые две из рассмотренных разновидностей принадлежат дискретно-непрерывным сигналам, а третья – дискретному сигналу. Последний называется также цифровым, так как дискретные значения сигнала обычно представляются в цифровой форме.

Рассмотрим некоторые вопросы, связанные с точностью представления непрерывных сигналов Х(t) в результате дискретизации во времени и квантования по уровню.

В результате дискретизации во времени исходный непрерывный сигнал Х(t) представляется конечной последовательностью отдельных значений Х(t_i), измеренных с шагом дискретизации ∆t=t_i-t_i-1. По значениям Х(t_i) можно восстановить исходный сигнал Х(t) с некоторой погрешностью. Функцию Х(t), полученную в результате восстановления (интерполяции) по значениям Х(t_i), называют воспроизводящей. При дискретизации возникает вопрос о точности преобразования, которая очевидно зависит от частоты отсчетов функции f_k=1/∆t_i, т.е. от выбранного шага дискретизации ∆t_i. С одной стороны, очевидно, что с уменьшением (увеличением) ∆t_i точность преобразования будет расти (уменьшаться) за счет увеличения (уменьшения) количества отсчетов. С другой стороны, очевидно, что нет смысла стремиться всегда брать отсчеты как можно чаще, независимо от вида сигнала Х(t), так как в случае медленно изменяющегося сигнала Х(t) два соседних значения Х(t_i) и Х(t_i+1) могут быть настолько связаны (коррелированны) между собой, что по одному из них Х(t_i) можно прогнозировать другое Х(t_i+1), т.е. никакой новой информации о сигнале при его последующем восстановлении по отсчетам это не дает. Проблема обеспечении точности дискретизации может быть сформулирована следующим образом: с каким максимальным интервалом необходимо брать отсчеты значений сигнала Х(t_i), чтобы не пропустить существенных его изменений или, другими словами, какое минимальное количество отсчетов необходимо брать для обеспечения заданной точности воспроизведения сигнала Х(t). От этого, в конечном счете, зависит количество информации, которую надо хранить и преобразовывать в вычислительном устройстве.

Возможны различные пути решения указанной проблемы.

В общем виде задача о представлении некоторого сигнала, являющегося непрерывной функцией времени, в виде конечного числа значений, взятых для дискретных значений времени, решена В.А. Котельниковым. В двух теоремах В.А. Котельников применительно к системе передачи сообщений по линии связи определил, как следует выбрать частоту дискретизации, обеспечивающую по полученным дискретным данным последующее воспроизведение исходного сигнала с заданной точностью.

Теорема 1. Любую функцию Х(t), имеющую спектр частот от 0 до f_m, можно представить суммой функции sinx/x, т.е. рядом:

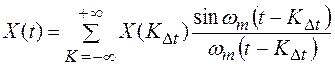, (1.51)

где K – целое число,

C 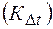– отсчеты мгновенных значений функции Х(t) с шагом дискретизации ∆t,

ω_m = 2πf_m, f_m – максимальная частота в спектре частот сигнала Х(t), Гц

ω_m – круговая частота.

Из этой теоремы может быть сделан и обратный вывод: любая функция, представленная рядом Котельникова (1.51), имеет спектр, состоящий из частот от 0 до f_m.

Теорема 2. Любая функция Х(t), содержащая частоты от 0 до f_m, полностью определяется дискретными значениями этой функции, следующими друг за другом с частотой 2f_m, т.е. через интервал 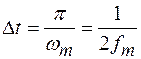сек. Таким образом, передачу непрерывного сигнала Х(t) с ограниченным спектром частот, поступающего от какого-либо датчика, можно свести к передаче последовательности дискретных чисел – значений этого сигнала, взятых через интервал времени 1/2f_m; число этих значений равно 2f_m. Через полученные значения ординат, при обработке результатов измерений, можно провести единственным способом воспроизводящую непрерывную функцию. Поэтому, проще говоря, нет смысла брать отсчеты чаще, чем интервал 1/2f_m, так как никакой новой информации о функции при ее последующем восстановлении по отсчетам это не дает. Следует подчеркнуть, что сказанное справедливо только в том случае, если в получаемой информации действительно отсутствует частоты выше f_m.

Теоремы В.А. Котельникова, являющиеся основой современной теории передачи сообщений, очень удобны для исследования всевозможных линий связи, вследствие того, что для этих линий известны частотные характеристики, а спектр передаваемых сигналов ограничен. Другое дело – реальные сигналы, имеющие конечную длительность Т. Для их точного представления, в отличие от моделей сигналов с ограниченным спектром (1.51), необходим спектр, который простирался бы от нуля до бесконечности. Теоретически, чтобы избежать погрешности дискретизации, для такого спектра требуется бесконечно большая частота взятия отсчетов. Практически выбирают такую частоту дискретизации, при которой погрешность не превышает заданной величины В этой связи теорему 2 В.А. Котельникова можно рассматривать как приближенную для функций с неограниченным спектром. На практике частоту отсчетов часто определяют как 2f_mk, т.е. интервал между отсчетами

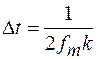(1.52)

где f_m – максимальная допустимая частота в спектре сигнала Х(t)

k – коэффициент запаса (обычно 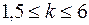). Так как безграничный частотный спектр заменяется ограниченным, вне которого спектральная плотность принимается равной нулю, то погрешность дискретизации будет определяться соотношением составляющих, лежащих внутри спектра и вне его.

Другой, практически легко реализуемый путь определения оптимального интервала дискретизации ∆t непрерывного сигнала Х(t) заключается в построении автокорреляционной функции сигнала и нахождении интервала корреляции τ_к .Дискретные отсчеты, взятые через интервал ∆t=τ_к, будут независимыми и информативными; для их обработки могут быть использованы методы математической статистики.

В случае, когда непрерывный сигнал Х(t) представлен своими дискретными значениями, полученными при равномерной или неравномерной дискретизации, он может быть заменен некоторой приближающей (аппроксимирующей) зависимостью. В общем случае исходный сигнал может быть аппроксимирован специальной функцией или полиномом, график которого проходит через известные дискретные значения. Наиболее часто используются степенные алгебраические полиномы, но так как обычно исходный сигнал задается в графическом или табличном, а не в аналитическом виде, то проведение аппроксимации полиномами с порядком выше первого затруднительно. При аппроксимации полиномом первого порядка все точки кривой, соответствующие дискретным моментам времени, соединяются отрезками прямых (кусочно-линейная аппроксимация). Алгебраические полиномы удобны для программирования и обработки с помощью вычислительной техники

При квантовании исходного сигнала по уровню возникает погрешность квантования. Так как в процессе преобразования значение сигнала Х(t) обычно отображается ближайшим уровнем квантования Х_m, то все значения, кроме кратных Х, представляются с некоторой погрешностью, максимальное значение которой равно 0,5 .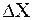

В заключение этого параграфа отметим, что дискретизация и квантование находят широкое применение в преобразователях информации, используемых для связи вычислительных устройств с реальными объектами.