Сигналы детерминированные и случайные.

Детерминированным называется сигнал, значения которого в любые моменты времени являются известными величинами. В противном случае сигнал называют случайным или стохастическим (от греческого слова stochastic – догадка). Каждый конкретный вид случайного сигнала Х(t), представляющего собой функцию времени, называют реализацией. Каждую реализацию можно представить бесконечной совокупностью зависимых или независимых случайных величин.

Случайный сигнал описывается статистически с помощью различных вероятностных характеристик.

Предположим, что имеется N реализаций случайного сигнала. Зафиксировав аргумент t (t = t_i) получим N значений случайной величины ξ.

Задание вероятностей ее возможных значений эквивалентно заданию так называемой функции распределения (интегрального закона) F_ξ(x,t_i). Значение функции распределения F_ξ(x,t_i) в точке х есть вероятность того, что случайная величина ξ примет значение меньшее или равное х, т.е.

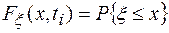(1.1)

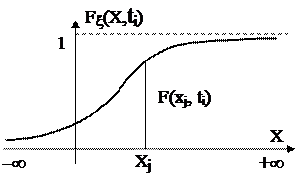Рис. 1.1. Функция распределения случайной величины (интегральный закон)

Для получения одной ординаты функции распределения, например F(x_j, t_i) для x=x_j (рис. 1.1) нужно подсчитать отношение числа раз n, когда значение ξ во всех N реализациях оказывались меньше или равными заданной величины x_j, к общему числу N значений ξ, т.е. n/N. Это отношение называется частотой, а предел этого отношения при N®∞ называется вероятностью того, что случайная величина ξ будет меньше или равной величины x_j, т.е. 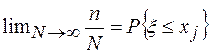. Очевидно, что если менять значения х, то и частота (вероятность) будет меняться, причем при х® -∞ F_ξ(-∞,t_i)=0, а при х®∞ F_ξ(∞,t_i) =1 (n=N), т.е. 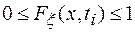. Функция распределения является полным статистическим описанием случайной величины в том смысле, что по ней можно определить все возможные значения случайной величины и соответствующие им вероятности. Например, вероятность того, что случайная величина ξ находится в интервале {x₁,x₂}

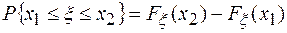
Случайная величина ξ описывается также плотностью распределения (дифференциальным законом)

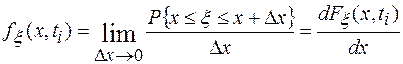(1.2)

В качестве примера на рис. 1.2 показана функция f_ξ(x,t_i). Имея N значений случайной величины можно построить ступенчатую функцию – гистограмму распределения случайной величины (ступенчатая функция на рис. 1.2). Для этого область изменения х разделяют на определенное число интервалов ∆х и каждому интервалу ставят в соответствие отношение n/N для этого интервала. При уменьшении интервала ∆х функция будет приближаться к непрерывной.

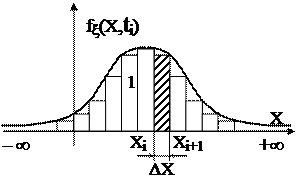
Рис. 1.2. Плотность распределения случайной

величины (дифференциальный закон)

Из (1.2) следует, что

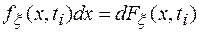или

,

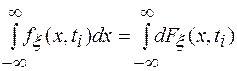
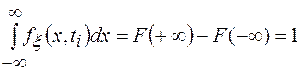т.е. площадь, ограниченная функцией f_ξ(x,t_i) и осью х равна 1. С помощью функции f_ξ(x,t_i) можно приближенно подсчитать вероятность того, что в момент времени t_i случайная величина ξ находится в интервале {x,x+∆x}:

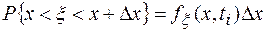
(заштрихованная площадь на рис. 1.2).

Отметим, что случайные величины, функции распределения которых дифференцируемы по х при любых х, называются непрерывными.

В ряде случаев нет необходимости полного описания случайной величины ее функцией распределения. Большинство практических задач можно решать с помощью немногих усредненных характеристик распределения m_n, образующихся из моментов ν порядка случайной величины ξ относительно числа а – т.е. математического ожидания случайной величины (ξ-а)^ν.

m_n=M(ξ-а)^ν, (1.3)

где М – обозначает операцию математического ожидания. Начальный момент первого порядка (ν=1) определяется относительно а = 0 и называется математическим ожиданием случайной величины ξ, т.е. m₁=M(ξ)=a.

Центральный момент второго порядка (ν=2) определяется относительно центра распределения и называется дисперсией случайной величины ξ, т.е. D_ξ=M(ξ-a)².

Математическое ожидание и дисперсия дискретной случайной величины ξ определяются по формулам:

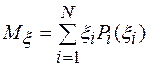(1.4)

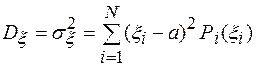(1.5)

В случае непрерывной величины ξ:

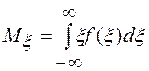(1.6)

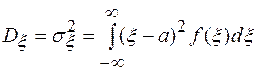, (1.7)

где 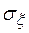обозначает среднеквадратичное отклонение случайной величины.

Математическое ожидание M_ξ и дисперсия D_ξ являются функционалами, описывающими свойства распределения случайной величины ξ : M_ξ характеризует «средневзвешенное» положение величины ξ, а D_ξ – ее рассеяние относительно математического ожидания.

Рассмотренные характеристики F_ξ(x,t_i) и f_ξ(x,t_i) являются одномерными, т.к. они получены при фиксированном значении аргумента t=t_i. Более полной характеристикой случайного сигнала х(t) является двумерный закон распределения f_ξ(x,t₁;x,t₂), заключающий в себе связь между значениями функции в два момента времени. Очевидно, что наиболее полной характеристикой случайного процесса мог бы служить только «бесконечномерный» (n-мерный) закон распределения (в силу непрерывности аргумента – времени) f(x,t₁;x,t₂;…x,t_n). Однако на практике существуют и лучше изучены некоторые типы случайных сигналов, свойства которых полностью определяются законом распределения при малом числе n (обычно для n < 3). К такому классу случайных сигналов относятся чисто случайные сигналы, характеризующиеся независимостью значений х(t) в различные моменты времени (для таких сигналов f_ξ(x,t₁;x,t₂,…,x,t_n)= f_ξ(x,t₁)· f_x(x,t₂)·…f_ξ(x,t_n). Чисто случайный процесс является идеализацией, т.к. в реальных процессах всегда существует статистическая связь между значениями х(t) в достаточно близкие моменты времени. Другим примером являются марковские (по имени математика А.А. Маркова) случайные сигналы, для которых, в силу их безынерционности, любая n – мерная плотность вероятности их значений может быть получена из двумерной плотности вероятности.

Получение многомерной плотности вероятности в общем случае представляет собой весьма трудную задачу. Поэтому для многих практических областей применения при определении статистических характеристик случайного сигнала, как и случайной величины, вполне достаточно знания некоторых интегральных (усредненных) характеристик, но вместо моментов порядка ν в случае случайных величин, моментных функций различных порядков ν

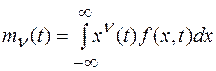(1.8)

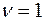
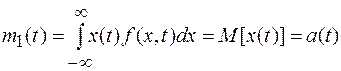При (1.9)

Эта функция времени называется математическим ожиданием случайного сигнала х(t). Очевидно, что математическое ожидание случайного сигнала представляет собой некоторую среднюю кривую, около которой располагаются его возможные реализации.

Сигналы вида 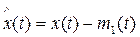обычно называют центрированными. Начальная моментная функция второго порядка (ν=2) характеризует математическое ожидание квадрата процесса, т.е. M[x²(t)], а центральная моментная функция второго порядка (ν=2)

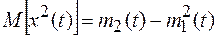(1.10)

носит название дисперсии

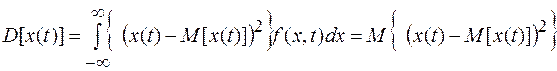. (1.11)

Корреляционной (автокорреляционной, автоковариационной) функцией называют математическое ожидание произведения

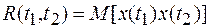. (1.12)

Случайные сигналы принято разделять на нестационарные (статистические характеристики зависят от начала отсчета времени) и стационарные. Строго говоря, стационарные случайные сигналы, как и стационарные физические системы, не существуют. Однако, стационарные случайные сигналы являются очень «удобной» идеализацией и в практических задачах играют чрезвычайно большую роль. Стационарными случайные сигналы могут быть в «большей или меньшей степени»: в узком и широком смысле. Стационарность в узком смысле – полная стационарность; в этом случае все плотности вероятности значений случайного сигнала не зависят от положения начала отсчета, т.е. не зависят от одинакового временного сдвига t₀ всех точек t₁, t₂…t_n вдоль оси времени:

.

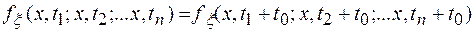Стационарность в широком смысле предполагает, что на случайный сигнал накладывается наименьшие ограничения. Это сигнал, статистические характеристики которого не зависят от времени, – математическое ожидание постоянно, а корреляционная функция зависит только от аргумента 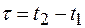, т.е.

.

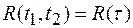В дальнейшем изложении, если не будет сделано специальных оговорок, речь будет идти о стационарных, в широком смысле, сигналах.

Среди стационарных случайных сигналов выделяют особую группу эргодических сигналов, которые подчиняются эргодическое теореме. Эта теорема гласит о том, что для эргодических сигналов результаты усреднения по множеству реализаций совпадают с их средними значениями на бесконечно большом интервале времени одной единственной реализации. Отсюда следует вывод о том, что для эргодических сигналов всегда можно выбрать такую конечную длину реализации, результаты усреднения по которой, совпадут с выборочной средней оценкой, полученной по заданному числу реализаций. Последнее положение особенно важно в области измерений статистических характеристик случайных сигналов, поскольку измерительная процедура и аппаратурная реализация различных алгоритмов в этом случае значительно упрощаются.

Для эргодических сигналов (далее, при отсутствии специальных оговорок, речь будет идти только о них) справедливы следующие определения.

Математическое ожидание определяется как среднее по времени

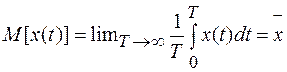. (1.13)

Дисперсия (мощность)

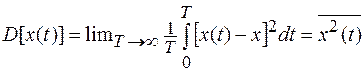(1.14)

Корреляционная функция

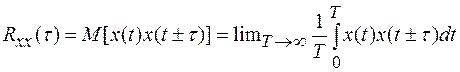(1.15)

Для центрированных сигналов корреляционная функция:

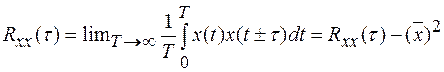(1.16)

При аппаратурном определении числовых характеристик случайных сигналов часто пользуются приближенным значением – оценкой (здесь и далее для обозначения оценок используется знак «звездочка»):

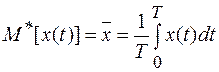(1.17)

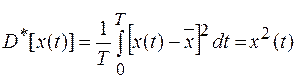(1.18)

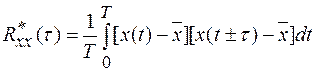(1.19)

или для центрированного сигнала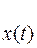

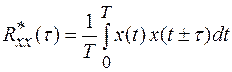(1.20)

Выражение (1.17) определяет оценку математического ожидания – среднего значения случайного сигнала. Наиболее близким к нему, в случае сигнала, заданного N значениями х_i, является среднее арифметическое N значений случайного сигнала или выборочное среднее (рис. 1.3)

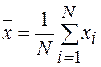(1.21)

Рис 1.3. Оценка математического ожидания случайного сигнала

Выражение (1.18) дает оценку дисперсии 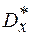, которая характеризует разброс значений х_i от математического ожидания. Наиболее близким к нему в случае сигнала, заданного N значениями x_i, является среднее арифметическое квадратов N центрированных значений случайного сигнала или выборочная дисперсия

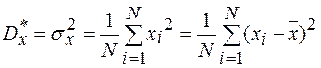(1.22)

где 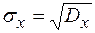- среднеквадратическое отклонение.

Выражение (1.19) дает оценку корреляционной функции. Практически, для нахождения одного ее значения например, 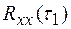для 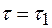, по одной реализации случайного сигнала х(t) (рис. 1.4а) нужно взять определенное количество произведений значений х(t), отстоящих друг от друга на величину 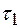, и найти их среднее арифметическое, т.е.

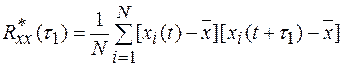
а) б)

Рис. 1.4. Построение корреляционной функции R_XX (τ), для значения τ=τ₁

Величина 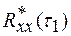(рис. 1.4б) показывает среднюю силу статистической связи случайных значений сигналов х₂ и х₁, х₄ и х₃, х₆ и х₅ и т.д., отстоящих друг от друга на интервал 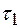. Если величина 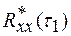большая – то и сила связи большая (зная одно значение сигнала можно предсказать другое), если величина 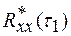мала – то и статистическая связь этих значений мала (зная одно значение сигнала, например х₁, трудно прогнозировать другое – х₂). Аналогичным образом могут быть определены значения корреляционной функции для других значений 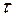. Для автоматического измерения множества ординат автокорреляционной функций используются специальные приборы – коррелометры.

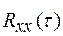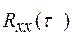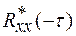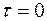
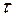Из (1.19), (1.20) следует, что является четной функцией, т.е. = При максимальна и равна оценке дисперсии, т.е. . С увеличением статистическая связь между двумя значениями случайного сигнала ослабевает и при .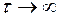

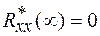Размерность корреляционной функции, как следует из (1.19) (1.20) равна квадрату размерности случайного сигнала. Практически это не всегда удобно (например, при сравнении корреляционных функций двух различных сигналов). Поэтому пользуются понятием нормированной (безразмерной) корреляционной функции 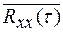, получаемой делением корреляционной функции на дисперсию:

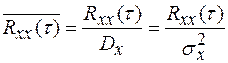(1.23)

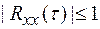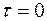
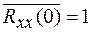Очевидно, что . При ; при 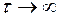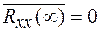. Примерный вид нормированной корреляционной функции показан на рис. 1.5.

Рис. 1.5. Нормированная корреляционная функция

Для случайных сигналов можно найти такой интервал времени 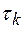, что при 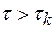значения сигналов x(t) и x(t+τ) можно считать независимыми. Интервал времени 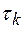, называемый интервалом корреляции, - это значение аргумента τ нормированной корреляционной функции, для которого (и всех больших значений) выполняется неравенство

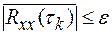
где ε - любая, сколь угодно малая положительная величина. Практически значение τ_k определяют, задавая ε значение, равное 0,05.

Интервал корреляции используется при определении шага дискретизации по времени при аналого-цифровом преобразовании и передаче сигналов, при оценке энтропии сигнала, при прогнозировании сигналов, при анализе и синтезе автоматизированных информационных систем.

Эквивалентное число N практически независимых отсчетов, обработанных за время T наблюдения за сигналом (например, при оценке математических ожиданий, корреляционных функций и др.) определяется частным от деления времени наблюдения Т на интервал корреляции 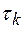, т.е.

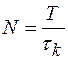(1.24)

Среди различных случайных процессов выделяют нормальный или гауссов процесс, полностью определяемый заданием математического ожидания и корреляционной функции. Такой процесс имеет место при действии большого числа независимых и непревалирующих факторов. Одномерная плотность вероятностей значений центрированного сигнала имеет вид

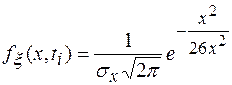
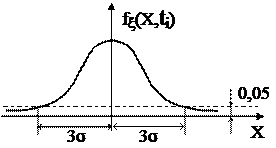Вероятность непопадания случайной величины в зону 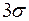составляет менее 0,05 (рис. 1.6).

Рис. 1.6. Плотность вероятностей нормального процесса

Практически часто встречаются случаи, когда исследуется не один случайный сигнал x(t), а система, состоящая из двух случайных сигналов x(t) и y(t). Одномерная функция распределения такой системы случайных величин

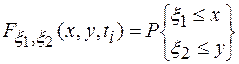(1.25)

Одномерная плотность вероятностей

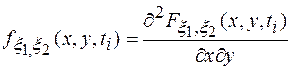(1.26)

При этом в общем случае

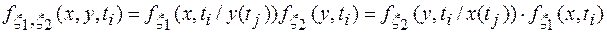
(1.27)

где 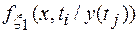- одномерная плотность вероятностей 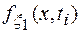при условии, что значение сигнала y(t) равно y(t_j);

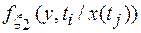- одномерная плотность вероятностей 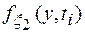при условии, что значение сигнала х(t) равно х(t_j).

В частном случае – независимых случайных сигналов х(t) и y(t) одномерная плотность вероятности 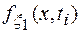не зависит от значения y(t_j) и

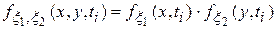(1.28)

Нахождение одномерной плотностей вероятности (1.27) представляет собой достаточно сложную задачу. Еще более сложную задачу – нахождение двумерной и более плотности вероятности системы двух случайных сигналов. Поэтому на практике используются более простые, хотя и менее информативные, рассмотренные выше числовые характеристики случайных сигналов. Для оценки взаимной корреляции двух случайных сигналов x(t) и y(t) пользуются понятием взаимной корреляционной (кросскорреляционной) функции R_xy(τ), которая характеризует силу статистической связи случайных значений этих сигналов, отстоящих друг от друга на интервал τ.

По аналогии с (1.19), (1.20):

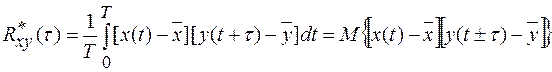(1.29)

Или для центрированных сигналов x(t) и y(t)

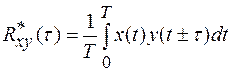(1.30)

При t=0 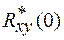максимальна и равна оценке взаимной дисперсии 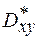, т.е. 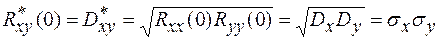.При 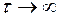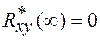, что означает независимость значений сигналов x(t) и y(t).

Размерность 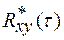равна произведению размерностей x(t) и y(t), что неудобно при сравнении взаимных корреляционных функций двух пар случайных сигналов. Кроме того 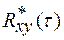характеризует не только статистическую связь x(t) и y(t) но и разброс значений этих сигналов относительно их математических ожиданий. Поэтому практически пользуются нормированной (безразмерной) взаимной корреляционной функцией:

(1.31)

Очевидно, что 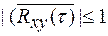(при τ=0 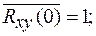при )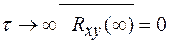

Отметим, что корреляционная функция R_z(t) случайного сигнала 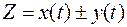, являющегося суммой (разностью) двух стационарных сигналов x(t) и y(t)

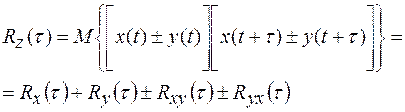(1.32)

При этом математическое ожидание суммы (разности) случайных сигналов равно сумме (разности) их математических ожиданий. В случае независимых сигналов (взаимная корреляционная функция равна нулю) корреляционная функция

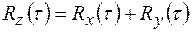(1.33)

При анализе информационных систем часто ставится задача определения периода измерения (дискретизации) Т входного x(t) и выходного y(t) случайного сигналов и определения времени сдвига δ_t^* измерений значений выходного сигнала по отношению к значениям входного сигнала.

Первая часть задачи решается путем нахождения интервалов корреляции 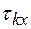(для x(t)) и 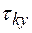(для y(t)), и выбору из них наибольшего, т.е. 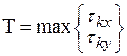(1.34)

Вторая часть задачи решается путем построения взаимной корреляционной функции .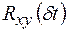

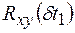Определение величины для одного значения временного сдвига, например для 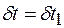(рис. 1.7а,б) практически осуществляется в соответствии с (1.29) путем вычисления среднего арифметического произведений

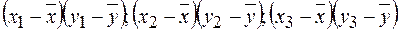и т.д.

а) б)

Рис. 1.7. Построение взаимной корреляционной функции R_XY (δt)

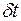Аналогичным образом могут быть получены величины для других значений и в конечном счете – взаимная корреляционная функция 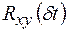(рис. 1.7б)) Максимуму этой функции соответствует интересующий нас временной сдвиг 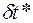, при котором действие значений x(t) (на входе системы) на значения y(t) (на выходе системы) проявляется с наибольшей статистической силой.

Значение 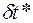дает сдвиг по времени измерения значений y(t) по отношению к измерению значений x(t).

На рис. 1.8 показаны входной x(t) и выходной y(t) случайные сигналы, период дискретизации Т и сдвиг 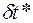между измерениями значений выходного и входного сигналов. Измеряемыми (дискретизируемыми) будут значения х₁, y₁; x₂, y₂; x₃, y₃ и т.д. .

При анализе случайных процессов наряду с корреляционными функциями широко применяются спектральные функции, которые характеризуют распределение энергии по частотным составляющим случайного сигнала. Наиболее широкое распространение среди таких функций получила спектральная плотность мощности 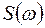, которая определяется, как производная по частоте от средней мощности (дисперсии) случайного процесса, определяемой выражением (1.14),

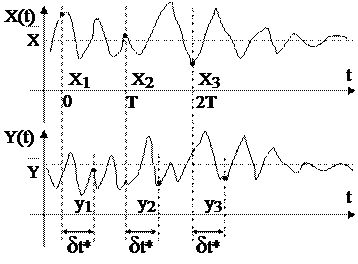
Рис 1.8. К определению измеряемых значений входного и выходного сигналов

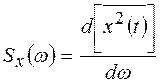(1.35)

Очевидно, что средней мощностью (средней интенсивностью, средним квадратом) процесса будет интеграл от спектральной плотности 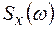, т.е.

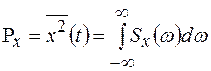(1.36)

Из определения (1.35) ясно, что функция 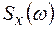характеризует плотность, с которой дисперсии отдельных гармонии (частотных составляющих) случайного процесса распределяются по спектру частот. Например, теоретически возможен случайный сигнал с постоянной спектральной плотностью 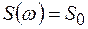в неограниченной полосе частот. Такой случайный сигнал называется белым или функциональным шумом. Реально такой сигнал создать нельзя. Поэтому практически ограничивают полосу частот, в пределах которых спектральную плотность можно считать постоянной. Практически считают, что если ширина частотного диапазона, в пределах которого спектральная плотность постоянна, по крайней мере на порядок больше полосы пропускания исследуемой системы, то этот источник для данной системы можно считать эквивалентом источника белого шума.

Спектральная плотность мощности 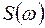и корреляционная функция 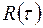для стационарного процесса, принимающего только действительные значения, связаны между собой прямым и обратным преобразованием Фурье

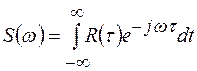(1.37)

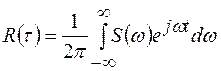(1.38)

Спектральная плотность представляет собой четную неотрицательную функцию частоты. Это обстоятельство дает возможность использовать на практике видоизмененные зависимости

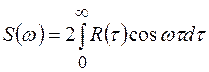(1.39)

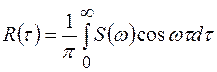(1.40)

Из приведенных выше взаимных преобразований Фурье следует:

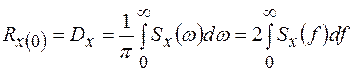(1.41)

где f - частота, Гц

Аналогично значение спектральной плотности на нулевой частоте определяется как

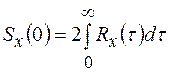(1.42)

Из приведенных формул следует, что для стационарных случайных процессов имеет место равенство

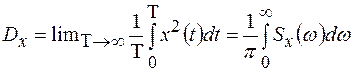(1.43)

Одной из общих характеристик случайных сигналов является ширина их энергетического спектра, определяемая отношением

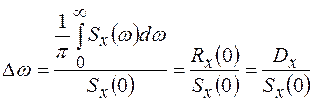(1.44)

Практически при моделировании различных стохастических систем средствами вычислительной техники часто возникает необходимость в специальных приборах - генераторах для получения реальных моделей случайных сигналов, имеющих заданные статистические характеристики – одномерную плотность вероятности и спектральную плотность (корреляционную функцию).

В связи с трудностями создания «специализированных» генераторов, воспроизводящих случайные сигналы с заданными статистическими характеристиками, обычно создают генераторы, воспроизводящие «типовые» случайные сигналы, а с помощью линейных и нелинейных преобразований обеспечивают получение случайных сигналов с заданными статистическими характеристиками.

Типовым принято считать случайный сигнал с одномерной плотностью вероятностей, подчиняющейся нормальному закону и со спектральной плотностью, постоянной в некотором диапазоне частот.

Выбор для типового случайного сигнала нормального закона распределения обусловлен тем, что этот закон наиболее широко встречается при анализе реальных систем, его проще всего воспроизводить и преобразовывать. Одномерная плотность вероятностей случайного сигнала и его спектральная плотность взаимосвязаны. При преобразовании одной из этих характеристик обычно изменяется и другая. Одним из наиболее важных исключений из этого правила является прохождение сигнала, имеющего нормальное распределение, через линейный фильтр. При этом закон распределения остается нормальным, а его спектральная плотность изменяется. Это свойство сигнала, имеющего нормальное распределение и используется в случае необходимости изменения его спектральной плотности.

Выбор для типового случайного сигнала характеристики спектральной плотности, постоянной в заданном диапазоне частот (белый шум) также обусловлен тем, что такой случайный сигнал может быть использован при анализе многих реальных систем, удобен при математическом описании стохастических задач; в то же время из такого сигнала могут быть получены случайные сигналы с различными спектральными характеристиками

Таким образом задача получения случайного сигнала Z(t), имеющего заданную спектральную плотность и одномерную плотность вероятности практически сводится к последовательному преобразованию типового сигнала x(t) генератора белого шума в 2 этапа:

1. получение на выходе линейного фильтра случайного сигнала y(t) с заданной спектральной плотностью и нормальным законам распределения;

2. получение на выходе нелинейного преобразователя случайного сигнала Z(t) с заданной одномерной плотностью вероятностей и полученной на 1-м этапе спектральной плотностью (рис.1.9).

Рис. 1.9. Блок-схема формирования случайного сигнала Z(t) с заданными спектральной плотностью и одномерной плотностью вероятностей

1. Для получения случайного сигнала с заданной спектральной плотностью используется зависимость спектральной плотности стационарного случайного сигнала S_вых(ω) на выходе линейной системы от спектральной плотности входного сигнала S_вх(ω) и частотной характеристики Ф(jω) линейной системы

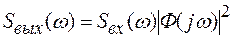(1.45)

Отсюда частотная характеристика Ф(jω) фильтра, обеспечивающего требуемую спектральную плотность на выходе S_вых(ω) при известной спектральной плотности S_вх(ω) сигнала на входе фильтра

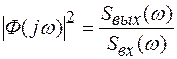(1.46)

Для входного сигнала, представляющего собой белый шум

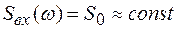
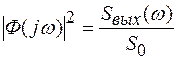(1.47)

Используя соотношения (1.39),(1.40), характеризующие функциональную связь корреляционной функции и спектральной плотности, можно однозначно связать параметры формирующего фильтра с параметрами корреляционной функции. После определения требуемой частотной характеристики Ф(jω) графическим или аналитическим методом и построения по ней передаточной функции фильтра он может быть реализован на различной элементной базе.

2. Преобразование непрерывного стационарного сигнала х(t) с одномерной плотностью вероятностей f(x) в сигнал y(t) с заданной плотностью вероятностей может быть осуществлено с помощью нелинейного преобразования

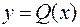(1.48)

где y – однозначная функция х.

Вероятности преобразования обоих сигналов в интервалах dx и dy одинаковы, поэтому

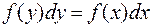(1.49)

или

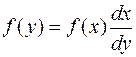(1.50)

Чтобы определить зависимость (1.48) необходимо найти такие значения у, которые при каждом значении х будут удовлетворять уравнениям (1.49) или (1.50). Определение зависимости (1.48) может быть выполнено аналитическим и графическим способами.

Корреляционные функции и спектральные плотности широко применяются в информатике при преобразовании, анализе, прогнозировании, идентификации и различении случайных сигналов, а также при анализе и синтезе автоматизированных информационных систем.