Правила відбору

Знаючи кількісне співвідношення для енергії електрона на енергетичному рівні в атомі водню, можна розрахувати весь його спектр. Нехай енергія більш високого збудженого енергетичного рівня дорівнює

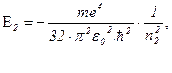(1.4.20)

а енергія нижчого рівня

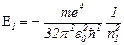. (1.4.21)

Частоти, які відносяться до різних спектральних серій, можна записати у вигляді

,

або врахувавши, що 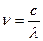, одержимо

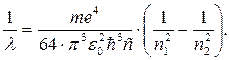(1.4.22)

Серія спектральних ліній, для якої n₁=1, називається серією Лаймана. Усі лінії цієї серії розміщені в ультрафіолетовій областей спектра електромагнетного випромінювання. У випадку, коли n₁=2, виникає друга серія випромінювання, яка називається серією Бальмера. Перші чотири лінії цієї серії знаходяться у видимій області спектра. Інші спектральні лінії цієї серії перебувають на межі видимої й ультрафіолетової областей спектра.

Формула (1.4.22) називається формулою Бальмера. У цій формулі вираз перед дужками є сталою величиною, яку називають сталою Рідберга. Стала Рідберга R розрахована з великою точністю. Її величина дорівнює

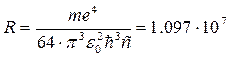м^-1.

Число знаків, до яких визначена стала Ридберга, показує рівень точності сучасної спектроскопії й ілюструє повний збіг розрахунків за формулою Бальмера з результатами спостережень.

Якщо n₁=3, то за формулою (1.4.22) можна розрахувати наступну серію випромінювання ─ серію Пашена. Усі лінії цієї серії перебувають у інфрачервоній області спектра.

Наступна серія випромінювання для n₁=4 носить назву серії Бреккета. Лінії цієї серії теж перебувають у інфрачервоній області спектра.

Кожному значенню енергії електрона в атомі водню E_n (за винятком Е₁) відповідає декілька значень хвильової функції 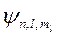. Вони відрізняються значеннями квантових чисел l i m_l. Це означає, що атом водню може мати однакове значення енергії і перебувати в кількох різних квантових станах.

Стани з однаковою енергією називаються виродженими, а число таких станів з одним значенням енергії, називається порядком виродження.

Порядок виродження легко обчислити виходячи з числа можливих значень l i m_l. Кожному значенню числа n відповідає 2l+1 значень квантового числа m_l. Тому число різних станів для даного значення n, дорівнює

. (1.4.23)

Таким чином кожен рівень енергії атома водню має порядок виродження 2n².

У квантовій механіці доводиться, що можливі лише такі переходи електронів між енергетичними рівнями, для яких виконується умова зміни орбітального квантового числа l на одиницю:

Dl=±1 . (1.4.24)

Умова, яка виражена співвідношенням (1.4.24) називається правилом відбору. Існування цього правила обумовлено тим, що фотон має власний момент імпульсу, який називають спіном, рівним наближено 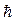. При випромінюванні фотон забирає від атома цей момент, а при поглинанні віддає атому. Тому правило відбору є відповідним наслідком закону збереження моменту імпульсу.

Переходи електронів в атомі водню, які дозволені правилом відбору показані на рис. 1.14.

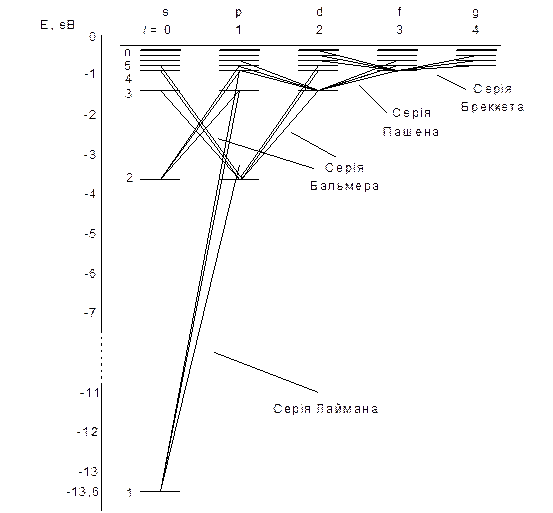
Рис. 1.14

Серії Лаймана відповідають переходи np®1s, (n=2,3,4,...).

Серії Бальмера відповідають переходи np®2s, ns®2p і nd®2p, (n=3,4,5,...).

Стан 1s є основним станом атома водню. У цьому стані атом має найменшу енергію. Для виведення атома з основного стану йому слід надати необхідну енергію за рахунок зовнішнього джерела. Таким джерелом енергії може бути нагрівання, електричний розряд або опромінення.

При опромінені водню фотонами від зовнішнього джерела їх енергія поглинається повністю лише у випадку коли енергія фотонів у точності збігається з різницею енергії двох енергетичних рівнів. У цьому випадку фотон зникає повністю, передаючи атому всю свою енергію. Атом не може поглинути частину фотона, оскільки фотон є неподільним.

1.4.3. Механічний і магнетний моменти атома водню

Орбітальне квантове число l визначає стан електрона в атомі. Якщо рух електрона характеризується значенням квантового числа l=0, то електрон перебуває в s-стані, а сам електрон називається s-електроном. Квантовому числу l=1 відповідає р-стан електрона, l=2 ― d-стан, l=3 ― f-стан і т. д.

Для електрона, що знаходиться в атомі водню на n-му

енергетичному рівні, можливі одна колова орбіта при l=n-1 i n-1

еліптичних орбіт. Із зменшенням l збільшується ступінь витягнутості орбіти. Отже, при заданому головному квантовому числі орбітальне квантове число l визначає форму орбіти.

У квантовій механіці орбітальний момент імпульсу електрона визначається таким співвідношенням:

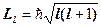, де (l=0,1,2,...n-1). (1.4.25)

Цей вираз свідчить про можливість таких рухів електрона, для яких (при l=0) орбітальний момент імпульсу електрона дорівнює нулю.

Третє квантове число m_l, яке називається магнетним квантовим числом, визначає просторовий розподіл траєкторії руху електрона, а також проекцію вектора механічного моменту або моменту імпульсу орбіти на заданий напрям.

Орбіту, по якій рухається електрон, можна розглядати як контур струму. Такий контур характеризується певним значенням орбітального магнетного моменту електрона 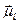, векторною величиною, що направлена вздовж осі орбіти в той бік, куди направлена індукція магнетного поля, створюваного цим контуром. Між вектором 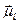і 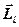існує такий зв’язок

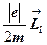= - =-g , (1.4.26)

де е ― заряд електрона; m ― маса електрона; g 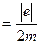― гіромагнетне відношення.

Враховуючи значення L_l із (1.4.25) одержимо:

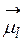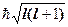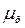
=-g = - 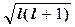, (1.4.27)

де 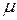_{б =} g 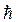― магнетон Бора.

Як видно з (1.4.26) вектори 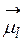і 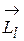мають протилежні напрямки.

Вектор 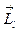може мати 2l+1 просторових орієнтацій, а це означає, що при даному l електрони в атомі, у зовнішньому магнетному полі, можуть рухатися по 2l+1 орбітах, які відрізняються своєю орієнтацією щодо напрямку магнетного поля

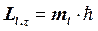, (1.4.3.4)

де m_l ― магнетне квантове число.

На рис. 1.15 зображено можливі значення проекції орбітального механічного моменту на напрям осі z зовнішнього магнетного поля для випадків l=1 i l=2.

Рис.1.15

Таким чином просторове квантування приводить до розчеплення в магнетному полі енергетичного рівня електрона на ряд підрівнів, а отже, і до розчеплення спектральних ліній. Таке явище спостерігав Зеєман. Розчеплення спектральних ліній також можливе в електричному полі ─ ефект Штарка.

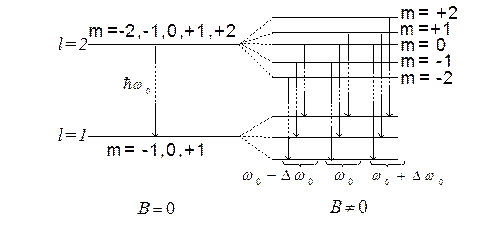
Рис. 1.16

Між розщепленими рівнями можливі переходи електронів у відповідності з правилами відбору (рис. 1.16)

Dl=±1 i Dm_l=0 ; ±1.