Розв’язком рівняння (1.3.55) може бути функція

, (1.3.56)

де А і В ─ деякі константи.

Експонента з додатним знаком фізичного змісту не має й може бути відкинута, тому що не повинно бути зростання імовірності в області потенціального бар’єра. Тому в області потенціального бар’єра (х>0), хвильова функція частинки Y_x визначається рівністю

Y_x = Аe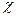^{- x} . (1.3.57)

Коефіцієнт А у виразі (1.3.57) пов’язаний з інтенсивністю променя частинок, які рухаються у напрямі бар’єра, а тому задається довільно. Як правило для х>0 координати частинок розподіляються з густиною імовірності

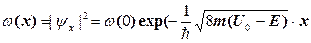, (1.3.58)

де w(0) дорівнює значенню |Y_x|² при х=0.

Рівняння (1.3.58) показує, що із збільшенням глибини проникнення в область потенціального бар’єра, густина імовірності w(х) зменшується експоненційно. Це зменшення буде тим швидше, чим більша різниця енергій U₀ - E.

Знайдемо глибину проникнення елементарної частинки в область потенціального бар’єра при умові, що m= 9,1 10^-31 кг (електрон), U₀ - E = 10^-4 eB, а густина імовірності w(х) на цій відстані зменшується в е разів

.

Ця відстань перевищує на два порядки діаметр атома водню. Глибина проникнення зменшується на порядок, якщо різниця енергій U₀ - E зросте до 10^-2 еВ.

Здатність квантових частинок проникати в область потенціального бар’єра приводить до тунельного ефекту. Його суть полягає в проникненні частинки з однієї області в іншу область, які поділені потенціальним бар’єром навіть в тих випадках, коли енергія частинки Е менша висоти потенціального бар’єра U₀.

Таке проходження частинки виявляється можливим дякуючи існуванню під бар’єром хвильової функції, яка «прокладає» шлях частинці на будь-яку відстань. Тунельний ефект є головною причиною a-розпаду радіоактивних ядер.