Потенціальна енергія класичного осцилятора знаходиться за формулою

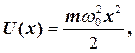(1.3.34)

де m ― маса частинки; 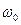― циклічна частота осцилятора.

Графічна залежність потенціальної енергії класичного осцилятора показана на рис. 1.8.

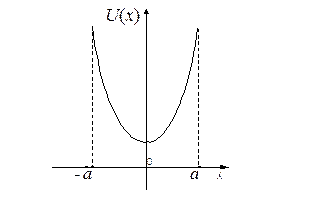
Рис. 1.8

.

З рисунка видно, що осцилятор може мати практично довільну енергію, навіть рівну нулю. В точках -а і +а кінетична енергія осцилятора дорівнює нулю, а потенціальна енергія досягає свого максимуму. За межі області (-а, +а) класичний осцилятор вийти не може.

Квантовим осцилятором може бути лише елементарна частинка, яка поряд із корпускулярними властивостями проявляє і хвильові властивості. Прикладом квантового осцилятора може бути коливний рух атомів і молекул у вузлах кристалічної гратки. Потенціальна енергія квантового осцилятора має ту ж математичну залежність, що і класичний осцилятор (1.3.34).

Стаціонарне рівняння Шредінгера для лінійного гармонічного осцилятора має вигляд:

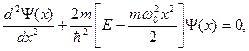(1.3.35)

де m ― маса квантової частинки; 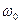― власна циклічна частота; Е ― повна енергія частинки.

Знаходження хвильових функцій квантового осцилятора є досить складною математичною задачею. Тому, опускаючи такі розв’язки, наводимо енергетичний спектр квантового осцилятора. Він має вигляд

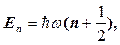(1.3.36)

де n= 0,1,2,3,... ― будь-яке ціле число, починаючи з нуля; 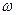― власна циклічна частота осцилятора; 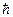― стала Дірака.

Аналіз рівняння (1.3.36) показує, що енергетичний спектр квантового осцилятора є дискретним і що власні значення енергії дорівнюють:

, ,

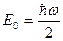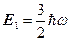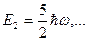
В енергетичному спектрі (1.3.36) проміжки між енергетичними рівнями не залежать від квантового числа n, а є однаковими

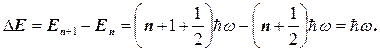(1.3.37)

Як показано на рис. 1.9, де енергетичний спектр квантового осцилятора суміщається з аналогічним спектром класичного осцилятора, квантовий осцилятор не має значень енергії рівних нулю.

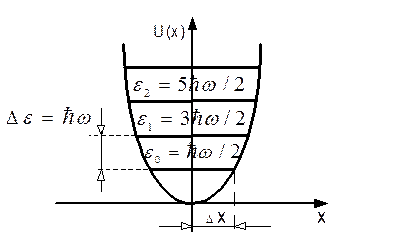
Рис.1.9

Найменше значення енергії квантового осцилятора дорівнює

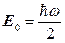. (1.3.38)

Меншої енергії квантовий осцилятор не може мати навіть при абсолютному нулі температур.

Покажемо наближеним способом, що енергія квантового осцилятора квантується. З рис 1.10 видно, що на відрізку l=2х₀ вкладається ціле число півхвиль де Бройля, тобто

(1.3.39)

де 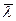― середнє значення довжини хвилі де Бройля.

Звідки

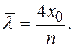(1.3.40)

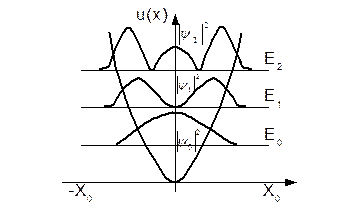
Рис. 1.10

Середнє значення імпульсу кванта хвилі де Бройля

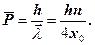(1.3.41)

Середня кінетична енергія такого осцилятора

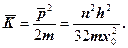(1.3.42)

Відомо, що повна енергія Е перевищує середнє значення кінетичної енергії у два рази, тобто

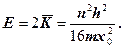(1.3.43)

З іншої точки зору повна енергія квантового осцилятора дорівнюватиме максимальній потенціальній енергії

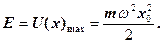(1.3.44)

Перемножимо рівності (1.3.43) і (1.3.44), одержимо

(1.3.45)

або

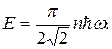(1.3.46)

В межах точності наших міркувань 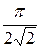»1, тому

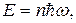(1.3.47)

де n =1,2,3,... ― цілі числа.

Наближений розрахунок показує, що енергія квантового осцилятора набуває ряду дискретних значень, тобто квантується.

Точне значення енергії для не збудженого квантового осцилятора нульового рівня можна одержати з рівняння Шредінгера (1.3.35), якщо згідно з рис. 1.10 скористатись функцією Гаусса, яка дорівнює

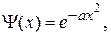(1.3.48)

де а ― стала величина, яку слід визначити.

Другу похідну від (1.3.48) підставимо в (1.3.35)

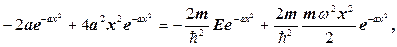
звідки

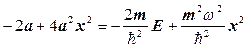. (1.3.49)

Тотожність (1.3.49) має місце у випадку рівності коефіцієнтів при х² і вільних членів, тобто

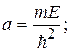
(1.3.50)

Система рівнянь (1.3.50) дає можливість одержати значення енергії Е і сталої величини а

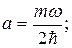
. (1.3.51)

Таким чином функція Гаусса є розв’язком рівняння Шредінгера (1.3.35) лише за умови коли .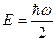

В цьому випадку

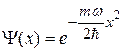. (1.3.52)

Слід відмітити, що оскільки відстань між суміжними рівнями енергії квантового осцилятора дорівнює то з урахуванням одержуємо енергетичний спектр квантового осцилятора у вигляді

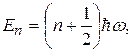(1.3.53)

де n = 0,1,2,3,...

1.3.4.Проходження частинки крізь потенціальний бар’єр.Тунельний ефект

Класична частинка не може перебувати в тих місцях, де її потенціальна енергія U(x) перевищувала б повну енергію частинки E. Щодо квантової частинки, то вона має таку властивість через те, що існує відмінна від нуля імовірність проникнення її крізь потенціальний бар’єр, тобто в область, де U(x) > E.

Проведемо оцінку цієї імовірності шляхом розв’язування такої задачі. Нехай квантова частинка з масою m, рухаючись в напрямі осі х, вдаряється в потенціальний бар’єр кінцевої висоти U₀, тобто

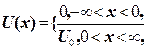
причому енергія частинки Е менша висоти бар’єра U₀, (рис. 1.11).

Рис. 1.11

В області потенціального бар’єра рівняння Шредінгера для стаціонарних станів набуде вигляду

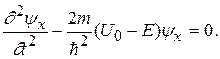(1.3.54)

Якщо позначити вира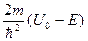з через , то рівняння (1.3.54) перепишеться

. (1.3.55)