Паралельна схема контролера нейромережевого керування
На рис. 5.6 наведена схема паралельного вмикання ШНМ як контролера для послідовної схеми керування.
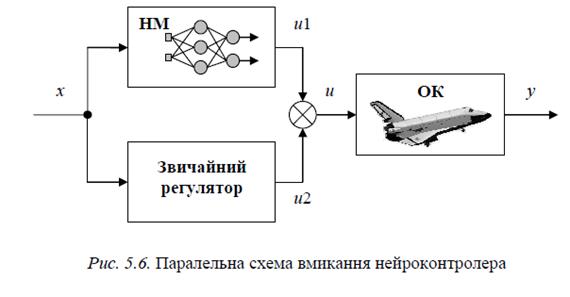
Навчання ШНМ полягає в тому, щоб скоригувати сигнал звичайного контролера u2, якщо він не забезпечує належної якості керування. Один із способів реалізації такого підходу зображено на рис. 5.7.
Такий підхід називають «навчанням із похибкою зворотного зв’язку».

У цій схемі ШНМ після завершення навчання приймає на себе керування об’єктом, усуваючи дію контролера зворотного зв’язку. Зазначимо, що зразковим регулятором у цьому випадку може виступати і людина-оператор.
5.4. Нейромережеве керування із зворотним зв’язком
Найпростіша схема нейромережевого керування із зворотним зв’язком подана на рис. 5.8.
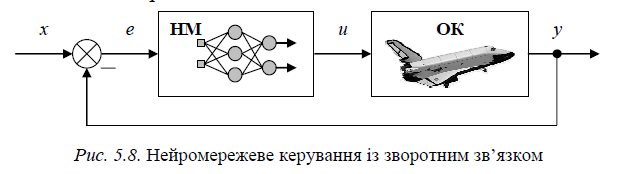
Нейронна мережа виконує функції регулятора замкненої системи.
Перевагою такої схеми є здатність забезпечувати високу якість керу-
вання за наявності неконтрольованих збурень, а також нестаціонарності і нестійкості ОК.
За такого підходу задача навчання ШНМ стає складнішою. Якщо для послідовної схеми керування відомо, що ШНМ має реалізовувати зворотну динаміку об’єкта, то в схемі зі зворотним зв’язком перетворення, яке має реалізовувати ШНМ, невідоме. Крім цього, ні зв’язок,ні якобіан зв’язку між показником якості регулювання і параметрами ШНМ невідомі. Система на рис. 5.8 не може навчатися в оперативному режимі.
Розглянемо більш складну схему керування. У схемі на рис. 5.9 використано контролер зворотного зв’язку, побудований з використанням мережі НМ1, що навчається через ідентифікатор НМ2.

Навчання через ідентифікатор, а не безпосередньо на об’єкті, потрібне для того, щоб не заважати нормальному функціонуванню об’єкта пробними впливами, які використовують у процесі навчання. До недоліків схеми можна віднести високі вимоги до обчислювальних ресурсів і можливі проблеми із стійкістю системи.
5.5. Схема із звичайним контролером, що керується нейронною мережею
У деяких системах використовують ідею настроювання параметрів звичайних регуляторів (наприклад, широковідомого ПІД-регулятора) для підвищення якості керування.
У системі, наведеній на рис. 5.10, ШНМ застосовують для настроювання параметрів ПІД-регулятора.
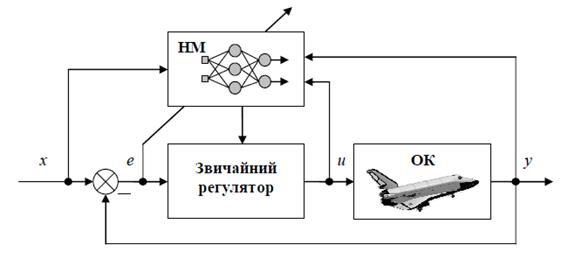
Рис. 5.10. Схема нейромережевого керування із самонастроюванням
5.6. Недоліки систем керування з нейромережами
Попри численні достоїнства, СК на основі ШНМ мають багато недоліків:
– під час оптимізації ваг ШНМ алгоритм навчання може зупинитись у локальному мінімумі, що зумовлює застосування алгоритмів глобальної оптимізації, які працюють досить повільно;
– немає строгої теорії щодо вибору типу і архітектури ШНМ, що спонукає до застосовування алгоритмів самоорганізації, які також працюють повільно;
– всю інформацію ШНМ отримує в процесі навчання і ніяку апріорну інформацію ввести в ШНМ неможливо.
6. НЕЧІТКІ МНОЖИНИ
6.1. Нечітка логіка. Історія виникнення
Теорія нечіткої логіки (fuzzy logic) була розроблена порівняно недавно. Лотфі Заде (Lotfi A. Zadeh), професор Університету Каліфорнії в Берклі і відомий тепер як засновник нечіткої логіки, зауважив, що традиційна двійкова комп’ютерна логіка не була здатна маніпулювати даними, котрі являють собою суб’єктивні або такі суто людські поняття, як «приваблива особистість» або «досить гаряче». І тому нечітка логіка була розроблена так, щоб дати змогу обчислювальним системам визначати розбіжності між даними «з відтінками сірого», аналогічно процесам людського мислення. У 1965 році Л. Заде опублікував свою фундаментальну роботу «Нечіткі множини», де описав математичну теорію нечітких множин і, як наслідок, нечітку логіку. Згідно з цією теорією, функції належності (або значення істина і неправда)відтепер визначались у діапазоні дійсних чисел від0до1.
Хоча сама технологія і з’явилась у Сполучених Штатах, тамтешні вчені й дослідники проігнорували її здебільшого через «незручну» назву. Вони відмовлялися прийняти те, що звучало настільки «по-дитячому», несерйозно. Деякі математики доводили, що нечітка логіка була ні чим іншим, як замаскованим поняттям імовірності.
І тільки останнім часом нечітка логіка стала однією з найбільш успішних сучасних технологій розроблення досконалих систем керування. Нечітка логіка ідеально підходить для розв’язання таких задач з тієї простої причини, що об’єднує досвід людини у вирішенні проблем із здатністю обчислюваних засобів подавати їх у вигляді точних розв’язків на основі повної або часткової інформації. Вона займає важливе місце серед методів проектування технічних систем, які не обмежуються
суто математичним підходом чи підходами, заснованими на чистій логіці (експертними системами).
Що ж являє собою «нечітка логіка»? Нечітка логіка – це надмножина традиційної (булевої) логіки, яка була розширена для того, щоб оперувати над частково істинними значеннями, розміщеними між «повна істина» і «повна неправда». Висновки в нечікій логіці швидше наближені, ніж точні. Важливість нечіткої логіки випливає з того, що більшість висновків, які робить людина, особливо ґрунтуючись на здоровому глузді, – неточні за своєю природою.
Найбільш суттєві такі характеристики нечіткої логіки:
– точний висновок є граничним випадком наближеного;
– все визначено лише в тій чи іншій мірі;
– будь-яку логічну систему можна розглядати у «нечіткому» сенсі, іншими словами, нечітка логіка є надмножиною традиційної логіки;
– знання інтерпретують як множину не жорстких або, що те ж саме, нечітких обмежень набору змінних;
– висновок розглядають як процес поширення нежорстких обмежень.
6.2. Класична теорія множин
Перед тим, як зайнятися детальним вивченням нечіткої логіки і нечітких множин, згадаємо, що являє собою класична «двозначна» теорія множин.
Множина – це набір об’єктів із спільними властивостями у певному контексті.
Наведемо декілька прикладів класичних множин:
– множина натуральних чисел, менших за 5: А = {1, 2, 3, 4};
– коло одиничного радіуса у комплексній площині: А = {z | z∈ C, | z |≤1};
– пряма на площині:
А = {(x, y) | ax + by + c = 0, (x, y, a, b, c) ∈ ℜ}.
Множина може бути задана (визначена) такими способами:
– переліком її елементів: A = {x1, x2, …, xn};
– заданням її властивостей: A = {x ∈ℜ| x ← P};
– функцією належності µА(х), яка за умови Х → [0, 1] має такий вигляд:
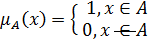
Множина дійсних чисел в діапазоні від 5 до 10: A = {x ∈ ℜ 5 ≤ x ≤ 10}. Графік функції належності такої множини подано на рис. 6.1.

µA
1 
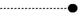
| x | ||||
Рис. 6.1. Множина дійсних чисел в діапазоні[5, 10]
У останньому прикладі числа, для яких функція належності набуває значення 1, ми інтерпретуємо як елементи, що належать множині, а числа, для яких значення функції дорівнює 0, як такі, що не належать множині.Такої концепції задання та інтерпретації множинзазвичай достатньо для більшості застосувань. Проте, не важко знай-ти ситуації, в яких такому підходові вже не вистачає «гнучкості». Наприклад, розглянемо множину «молодих людей». Задавши верхню вікову межу поняття «молодий» у 20 років (нижня, природно, 0), маємо таку функцію належності (рис. 6.2).
цьому випадку, додержуючись традиційної логіки, якщо вік індивідуума без одного дня 20 років, то він молодий, а наступного дня – вже ні. Бачимо, що в наведеному прикладі традиційна логіка не здатна адекватно відобразити реальної ситуації.
µA

1 
0 10 20 30 t
Рис. 6.2. Функція належності множини«молоді люди»
6.3. Елементи нечітких множин
Природним вирішенням подібної проблеми може бути послаблення жорсткості верхнього обмеження на належність множині. Задамо функції належності таким чином:
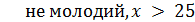
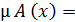
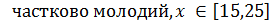
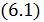
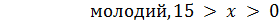
Графік функції належності (6.1) наведено на рис. 6.3.
µA

1 
0 10 20 30 t
Рис. 6.3. «Нечітка»функція належності
У цьому випадку можна сказати, що коли вік людини 15 років, то ступінь належності до множини «молодий» дорівнює 1, якщо 20 років, то ступінь належності 0,5, а якщо вік більший за 25, то 0.
Таким чином, нечіткій множині можна дати таке визначення: Нечіткою множиною A в деякому (непорожньому) просторі X, що
позначається як A ⊆ X , називається множина пар A = {(x,µA (x)); x ∈ X }, де µ A : X →[0, 1] – функція належності нечіткої множини А.
Ця функція приписує кожному елементу x ∈ X міру його належності до нечіткої множини А. При цьому можна виділити три випадки:
1) µA (x) =1 означає повну належність елемента x до нечіткої множини А, тобто x ∈ A ;
2) µA (x) = 0 означає, що елемент х не належить до нечіткої множини А, тобто x ∉ A ;
3) 0 < µA (x) <1 означає часткову належність елемента х до нечіткої множини А.
6.4. Види функцій належності та їх побудова
Для визначення вигляду функції належності розроблено різні експертні методи. У деяких випадках використовують типові форми функцій належності. Тоді методом експертних оцінок визначають тип функцій належності і їх параметри. Наведемо деякі типові функції належності.
Кусково-лінійні (трапецієподібні і трикутні)

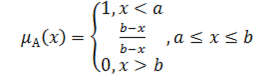
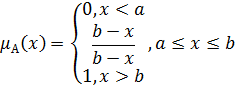

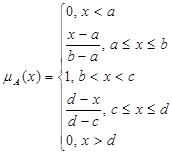 (6.2)
(6.2)
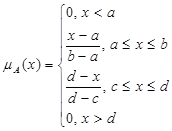 (6.3)
(6.3)
Бачимо, що трикутна функція належності (6.3) є частинним випадком узагальненої трапецієподібної (6.2).
S-подібні та дзвоноподібні

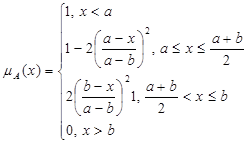
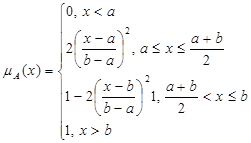

 (6.4)
(6.4)
Слід зазначити, що дзвоноподібна функція належності (6.4) не обов’язково повинна бути симетричною.
Розглянемо приклад побудови нечітких функцій належності, виходячи з інформації, поданої у лінгвістичній формі.
Візьмемо, наприклад, таке словосполучення, як температура повітря.З погляду суб’єктивного сприйняття температури людиною,вона може відповідати трьом рівням (множинам): холодно, тепло і гаряче.Процес переходу до нечітких множин схематично подано нарис. 6.4.

Дата добавления: 2015-08-26; просмотров: 1101;
