Навчання без вчителя (unsupervised training)

Розглянуті вище алгоритми навчання ШНМ за допомогою процедур зворотного поширення похибки, випадкового пошуку або генетичних алгоритмів припускають наявність деякої зовнішньої ланки, що надає мережі крім вхідних образів також і цільові вихідні образи. Алгоритми, що використовують подібну концепцію, називають алгоритмами навчання з вчителем. Для їх успішного функціонування потрібні експерти, які створюють на попередньому етапі для кожного вхідного образу еталонний вихідний. Оскільки створення штучного інтелекту розвивається шляхом копіювання природних прообразів, вчені не припиняють сперечатись щодо того, чи можна вважати алгоритми навчання з вчителем натуральними, чи вони повністю штучні. Наприклад, навчання людського мозку, на перший погляд, відбувається без вчителя: на зорові, слухові, тактильні та інші рецептори надходить інформація ззовні, і всередині нервової системи відбувається певна самоорганізація. Однак не можна заперечувати й того, що в житті людини немало вчителів – і в буквальному, і в переносному сенсі, – тих, що координують зовнішні впливи. Проте, чим би не закінчилася су

перечка прихильник і цих двох концепцій навчання, вони обидві мають право на існування.

Головна перевага навчання без вчителя – це його «самостійність». Процес навчання без вчителя, як і навчання з вчителем, полягає у підстроюванні ваг синапсів. Деякі алгоритми, однак, змінюють і структуру мережі, тобто кількість нейронів і їх взаємозв’язки, але такі перетворення правильніше назвати більш широким терміном «самоорганізація», та в межах цього матеріалу ми їх не розглядатимемо. Очевидно, що підстроювати синапси можна тільки на основі інформації, доступної в нейроні, тобто його стану і вже наявних вагових коефіцієнтів. Виходячи із цієї думки і, що більш важливо, за аналогією з відомими принципами самоорганізації нервових клітин, побудовані алгоритми навчання Хебба.

Сигнальний метод навчання Хебба полягає в зміні ваг за таким правилом обчислень:

, (4.9)

де - вихідне значення i-го нейрона (n-1) шару; - ви хідне значення j-го нейрона шару n; 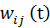та 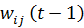- ваговий коефіцієнт сина пса, що з’єднує ці нейрони на ітераціях t і t-1 відповідно; a - коефіцієнт швидкості навчання. Тут і надалі, для загальності, літерою n позначають довільний шар мережі. Під час навчання за цим методом підсилюються зв’язки між збудженими нейронами.

Є також і диференціальний метод навчання Хебба:

, (4.10)

де y_i^{( n−1)} ( t ) і y_i^{( n−1)} ( t −1) – вихідне значення нейрона i шару n – 1 відповідно на ітераціях t і t – 1; 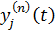і 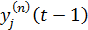- те ж саме для ней-

рона j шару n. Як видно з формули (4.10), найбільше навчаються синапси, що з’єднують ті нейрони, виходи яких динамічно збільшаться.

Повний алгоритм навчання у цьому випадку буде виглядати так:

Крок 1. Привласнення малих випадкових значень на стадії ініціалізації всім ваговим коефіцієнтам.

Крок 2. Подача вхідних образів на входи мережі і поширення сигналів збудження по всіх шарах відповідно до принципів класичних прямопоточних (feedforward) мереж, тобто для кожного нейрона розраховується зважена сума його входів, до якої потім застосовується активаційна (передатна) функція нейрона, в результаті чого отримується його вихідне значення.

Крок 3. Зміна вагових коефіцієнтів на основі отриманих вихідних значень нейронів за формулою (4.9) або (4.10).

Крок 4. Повторення, починаючи з кроку 2, доки вихідні значення мережі не установляться із заданою точністю.

Завершення навчання за новим способом, відмінним від використовуваного для мережі зворотного поширення, зумовлене тим, що підстроювані значення синапсів фактично не обмежені. На другому кроці циклу поперемінно подаються всі образи із вхідного набору.

Слід зазначити, що відгук на кожен з класів вхідних образів не відомий заздалегідь і являтиме собою довільне сполучення станів нейронів вихідного шару, зумовлене випадковим розподілом ваг на стадії ініціалізації. Разом з тим, мережа здатна узагальнювати схожі образи, визначаючи їх приналежність до одного класу.

5. НЕЙРОННІ МЕРЕЖІ В СИСТЕМАХ КЕРУВАННЯ