Поняття про критерії подібності. Кількість лінійно незалежних критеріїв подібності

В теорії подібності велике значення мають безрозмірні комплекси величин, які є добутком різних степенів цих величин. Їх називають критеріями подібності і позначають 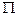. Критерії подібності використовуються як параметри, так і змінні досліджуваної системи. Скільки незалежних між собою критеріїв можна утворити з 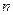розмірних величин? Незалежність 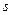величин означає, що

.

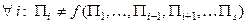Будемо розглядати електромеханічні системи з їх основними одиницями 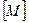, , 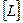, 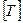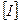. Нехай задано 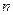величин 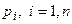. Тоді

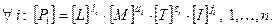
Будь-який критерій подібності – це деяка комбінація величин :

.

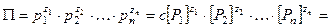
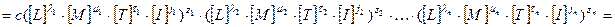
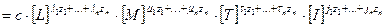Оскільки критерії подібності – величини нульової розмірності, то всі степені повинні бути рівні нулю, тобто:

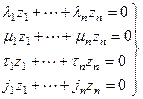. (3.1)

Таким чином, отримано систему з 4-х рівнянь, які містять 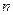невідомих 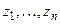. Як відомо, така система має 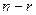лінійно незалежних розв’язків, де 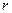- ранг матриці системи (5.1). Кожний розв'язок дає змогу отримати один критерій подібності

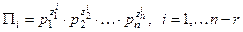. (3.2)

Ці 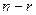незалежних критеріїв називають фундаментальними. Будь-який інший розв’язок системи (3.1) буде лінійно залежним та буде породжувати відповідний критерій подібності, який також буде залежним від фундаментальних критеріїв (3.2).

Отже, з заданих 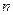величин можна побудувати 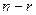незалежних критеріїв подібності, де 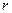- ранг матриці системи (3.1). Причому ранг матриці не може бути більшим від кількості основних одиниць. Загальне правило визначення рангу 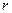можна сформулювати так: якщо серед заданих 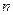величин вибрано 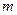первинних з незалежними розмірностями, то 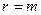, у протилежному випадку 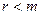. Кількість незалежних критеріїв подібності можна зменшити шляхом збільшення числа основних одиниць вимірювання, але лише при умові, розмірний коефіцієнт, що з’являється при цьому, не входить в рівняння, що описують систему.