Зонная структура твердых тел. Зоны Бриллюэна для кубических и генксагональных кристаллов.
Зоны Бриллюэна
вводятся в пространстве обратной решетки для определения минимального объема 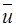 , которое содержит все значения компонент в.в.
, которое содержит все значения компонент в.в. 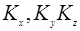 ; отвечающих физически неэквивалентным состояниям электрона в зоне (из-за периодичности в.ф).
; отвечающих физически неэквивалентным состояниям электрона в зоне (из-за периодичности в.ф).
Линейная одномерная решетка:
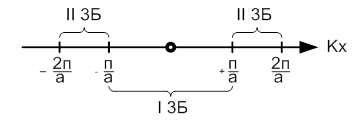
1-зоной Бриллюэна называют интервал значений: 
2-зона симметрично расположена вокруг 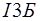 в интервале
в интервале  и
и  -интервал
-интервал 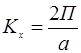
Первая 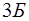 -называется приведенной
-называется приведенной 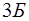 , т.к. любой
, т.к. любой 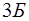 можно состояние
можно состояние 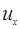 привести в
привести в 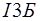 и наоборот учитывая периодичность энергии в
и наоборот учитывая периодичность энергии в 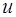 -пространстве.
-пространстве.
Т.е рассматривание состояний электрона в решетке можно ограничить 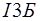 , а другие исключить, т.к они содержат другие эквивалентные состояния (физические)
, а другие исключить, т.к они содержат другие эквивалентные состояния (физические)
”0„ -центр зоны
Двухмерная (плоская) решетка
Размеры 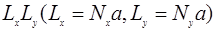 между трансляциями
между трансляциями 
Комп. в.в. 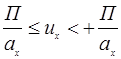 ;
; 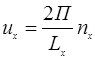 ;
; 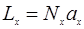 ;
; 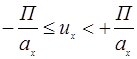
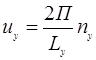 ;
; 
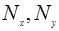 -число атомов
-число атомов
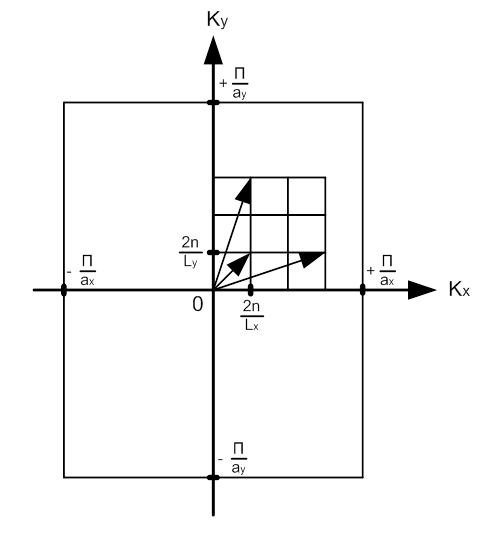
Средний вектор для состояния: 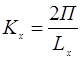
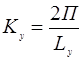
Все компоненты 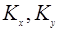 отвечающие неэквивалентным физическим постоянным, заключены в пределах первой зоны Бриллюэна с
отвечающие неэквивалентным физическим постоянным, заключены в пределах первой зоны Бриллюэна с 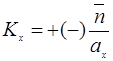 и
и 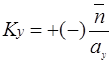 - тоже прямоугольная плоская решетка в К - пространстве.
- тоже прямоугольная плоская решетка в К - пространстве.
Трехмерный кристалл
Простой куб----обратная решетка----зона Бриллюэна
↓ ↓
Куб куб с объемом
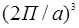
Гранецентрированная ОЦК→усеченный октаэдр
(куб)
Зона Бриллюэна
Минимальный по объему многогранник построенный симметрично относительно центра 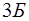 −точки
−точки 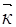 =0 и включающей все возможные неэквивалентные физические состояния для электрона в кристалле.
=0 и включающей все возможные неэквивалентные физические состояния для электрона в кристалле.
Основные точки в зоне Бриллюэна п/п Г, X, L
Минимумы энергии электронов в зоне проводимости п/п с алмазной решеткой и решеткой сфалерита лежат в центре 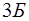 −точки
−точки 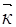 =0−”Г„ в направлениях [111]−”X„ точка и [100]−”L„ точка.
=0−”Г„ в направлениях [111]−”X„ точка и [100]−”L„ точка.
2.4 Эффективная масса электрона в кристалле, её связь со структурой энергетических зон. Понятие дырки. Динамика электрона в периодическом поле изитропных и анизотропных кристаллов.
Эффективная масса носителей заряда в телах
В кристалле на электрон действуют огромные силы со стороны кристаллического поля U( 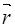 ),которые превосходят по величине внешние силы со стороны электрических и магнитных полей.
),которые превосходят по величине внешние силы со стороны электрических и магнитных полей.
Поэтому для описания динамики электрона под действием внешних полей с использованием законов механики для свободного электрона ввели понятие эффективной массы −m*
В эффективную массу m*”упрятали„ все внутренние силы 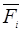 Электроны в кристалле ускоряются только под действием внешних сил
Электроны в кристалле ускоряются только под действием внешних сил 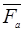 и m* связывает силу
и m* связывает силу 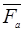 и ускорение
и ускорение 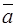 .
.
Введем m*:
E 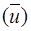 −закон дисперсии−непрерывная функция в пределах
−закон дисперсии−непрерывная функция в пределах 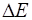 имеющая экстремуму в различных точках
имеющая экстремуму в различных точках 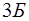 .пусть в точке
.пусть в точке  −находится экстремум функции E
−находится экстремум функции E 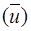 .
.
Разложим в ряд Тейлора функцию E 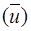 вблизи малой окрестности
вблизи малой окрестности 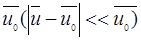
E 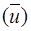 =E(
=E( 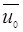 )+
)+ 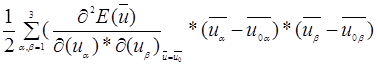

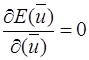 в точке
в точке 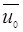 ,
,
где: 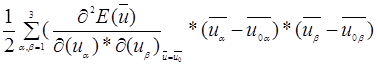 −вторая производная по векторному аргументу =тензору второго ранга.
−вторая производная по векторному аргументу =тензору второго ранга.
Запишем E 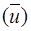 в форме аналогичной для свободного электрона: E(
в форме аналогичной для свободного электрона: E( 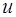 )=
)= 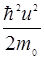 , где
, где 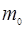 −массасвободного электронаE
−массасвободного электронаE 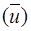 =E(
=E( 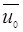 )+
)+ 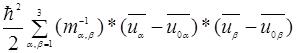 ,
,
где 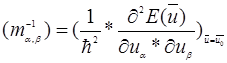 −тензор обратной эффективной массы−размерность.
−тензор обратной эффективной массы−размерность.
Обратной массы, т.к. размерность квазиимпульса совпадает с размерностью импульса.
( 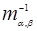 )−материальная константа веществапоэтому главные оси тензора обратной массы совпадают с главными осями (основными) симметрией кристалла.
)−материальная константа веществапоэтому главные оси тензора обратной массы совпадают с главными осями (основными) симметрией кристалла.
Запишем тензор ( 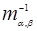 ) в главных осях, при этом
) в главных осях, при этом 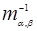 =
= 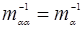
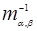 = [
= [ 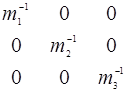 ], где
], где 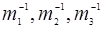 −главные значения тензора обратной эффективной массы.
−главные значения тензора обратной эффективной массы.
Запишем закон дисперсии в главных значениях тензора обратной эффективной массы:
E(  )=E(
)=E( 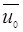 )+
)+ 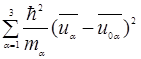 ,где:
,где: 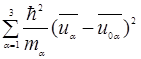 −кинетическая энергия электрона проводимости, имеющая разные массы по направлениям
−кинетическая энергия электрона проводимости, имеющая разные массы по направлениям 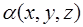 .
.
Величина 1: 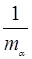 =
= 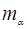 −компоненты эффективной массы по направлениям
−компоненты эффективной массы по направлениям 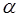 .
.
Понятие m*−неформальное ,т.е m* позволяет описывать динамику электрона в периодическом поле под действием внешних сил, но только для энергий в узком интервале, вблизи экстремумов в зоне.
О знаке m*
В близи минимума энергии в зоне (дно зоны) тензор обратной эффективной массы имеет положительный знак (  ), то эффективная масса электрона −положительна (
), то эффективная масса электрона −положительна ( 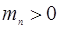 ), в близи максимума энергии в зоне (потолок зоны) −(
), в близи максимума энергии в зоне (потолок зоны) −( 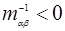 )− отрицательный знак, поэтому эффективная масса электрона отрицательна (
)− отрицательный знак, поэтому эффективная масса электрона отрицательна ( 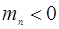 ).
).
Т.о у потолка зоны электрон будет как частица с отрицательной массой, что означает, что он ускоряется против направления действия внешней силы.
Электрон с 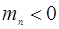 заменяют квазичастицей с положительным зарядом
заменяют квазичастицей с положительным зарядом 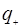 =
= 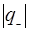 и положительной массой равной массе электрона.
и положительной массой равной массе электрона.
Такая частица ускоряется нормально −по направлению силы −называют дыркой
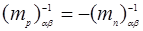
Анизотропный и изотропный квадратичные законы дисперсии
Введение m* позволяет записать в квадратичной форме законы дисперсии E(  ) для кристаллов различной симметрии, но вблизи экстремальных значений энергии, где справедливо понятие m*.
) для кристаллов различной симметрии, но вблизи экстремальных значений энергии, где справедливо понятие m*.


 Анизотропный закон дисперсии E(
Анизотропный закон дисперсии E(  )−эффективная масса−тензор.
)−эффективная масса−тензор.
Положим  , E(
, E(  )
) 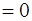 ,то E(
,то E(  )=
)= 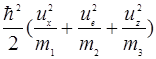
 Изотропный закон дисперсии−характерен для прямозонных п/п , для электронов вблизи точки (
Изотропный закон дисперсии−характерен для прямозонных п/п , для электронов вблизи точки ( 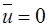 )−эффективная масса (скалярная величина).
)−эффективная масса (скалярная величина).
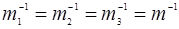
E(  )=
)= 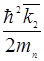 (1:
(1: 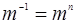 ),
), 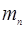 −изотропная величина
−изотропная величина
Анизотропный закон E(  )−характерен для электронов в зоне проводимости непрямозонных п/п.
)−характерен для электронов в зоне проводимости непрямозонных п/п.
E(  )=
)= 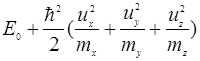
Оси x, y, z−главные оси симметрии кристалла и тензора обратной эффективной массы.
Поверхности равной энергии
E( 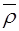 )=const или E(
)=const или E(  )=const
)=const
Используется для описания зонной структуры кристаллов наряду с законом дисперсии.
E( 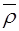 )=const−поверхность второго порядка(трехосный эллипсоид)
)=const−поверхность второго порядка(трехосный эллипсоид)
пусть экстремум E лежит в точке 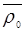
E( 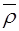 )=E(
)=E( 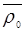 )+(
)+(  )
)
Запишем уравнение E( 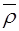 )=const в канонической форме:
)=const в канонической форме:

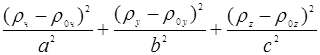 =1
=1
a, b, c −полуоси эллипсоида
 a=
a= 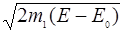 ; b=
; b= 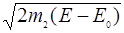 ; c=
; c= 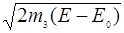
Если 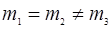 −имеем эллипсоид вращения.
−имеем эллипсоид вращения.
Если 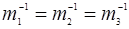 −то поверхность E(
−то поверхность E( 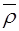 )=const−сфера (тензор вырождается в скалярную величину).
)=const−сфера (тензор вырождается в скалярную величину).
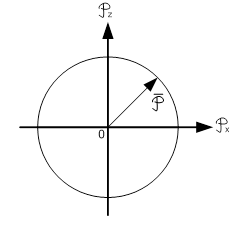
Физические свойства кристалла в этом случае изотропные, а в предыдущем случае анизотропные.
Динамика электронов в периодич. поле кристалла
Для описания динамики электрона используют классическую функцию Гамильтона, заменив импульс на квазиимпульс:

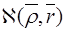 = E(
= E( 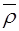 )+V(
)+V( 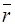 )
)
E( 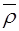 )−кинетическая энергия
)−кинетическая энергия
V( 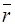 )−потенциальная энергия
)−потенциальная энергия
Скорость электрона V(  ) в разрешенном
) в разрешенном  − состоянии энергетической зоны
− состоянии энергетической зоны
Используем уравнение Гамильтона для скорости:
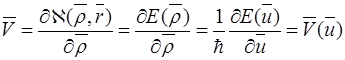
т.е. 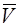 (
(  )−есть градиент энергии V(
)−есть градиент энергии V(  )−V(
)−V(  )=
)= 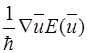
значение 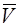 (
(  ) совпадает с групповой скоростью
) совпадает с групповой скоростью 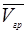 волнового пакета, отчего движение квантовой частицы с энергией
волнового пакета, отчего движение квантовой частицы с энергией 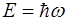 и импульсом
и импульсом 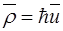
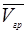 =
= 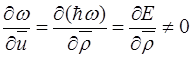
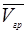 −равна квантовомеханической средней скорости
−равна квантовомеханической средней скорости
Особенности движения
V(  ) определяется градиентом E(
) определяется градиентом E(  ), поэтому вектор скорости
), поэтому вектор скорости 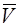 (
(  ) направлен по нормали к изоэнергетической поверхности E(
) направлен по нормали к изоэнергетической поверхности E(  ) = const
) = const
Если 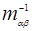 −тензор, то
−тензор, то 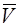 (
(  ) и
) и 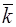 не совпадают по направлению.
не совпадают по направлению.
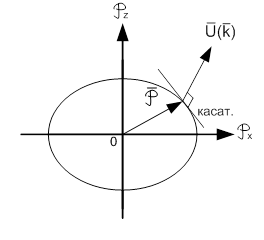
Вектор 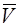 (
(  ) и
) и 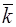 совпадают по направлению, если
совпадают по направлению, если 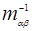 - скаляр, т.е. для свободного электрона.
- скаляр, т.е. для свободного электрона.

Особенности движения электрона у краев зон
У краев энергетических зон энергия электрона принимает экстремальные значения (E min и E max).
Поэтому 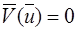 , т.е. электрону соответствует не бегущая волна (волна Блоха), а стоячая, при значениях
, т.е. электрону соответствует не бегущая волна (волна Блоха), а стоячая, при значениях 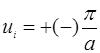 происходит отражение электронных волн от границ зоны Бриллюэна.
происходит отражение электронных волн от границ зоны Бриллюэна.
При приближении электрона к границе 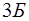 электронная волна тормозится решеткой и отражается. Стоячая электронная волна не участвует в переносе энергии.
электронная волна тормозится решеткой и отражается. Стоячая электронная волна не участвует в переносе энергии.
Скорость 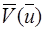 является нечетной функцией волнового вектора
является нечетной функцией волнового вектора 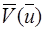 =
= 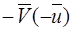 , поэтому средняя скорость
, поэтому средняя скорость 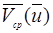 по всей зоне будет равна нулю.
по всей зоне будет равна нулю.
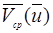 =
= 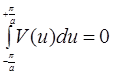 (интегрируем в симм. пределах)
(интегрируем в симм. пределах)
Т.о. при движении электронов, при отсутствии внешнего электрического поля не будет переноса зарядов, т.е. не будет возникать электрический ток.
Ускорение электрона в кристалле
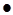 можно определить, как изменятся скорость во времени:
можно определить, как изменятся скорость во времени:
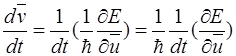
Предположим, эффективная масса это 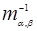 , найдем
, найдем 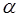 -компоненту ускорения;
-компоненту ускорения;
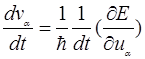
Энергия от t зависит через зависимость 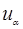 от t, поэтому:
от t, поэтому: 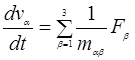
Вывод: при тензорной эффективной массе электрон под действием 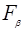 в направлении
в направлении 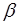 получает ускорение в направлении
получает ускорение в направлении 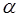 . Направления ускорения и силы будут совпадать, если
. Направления ускорения и силы будут совпадать, если 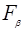 направлена вдоль главных осей тензора обратной эффективной массы.
направлена вдоль главных осей тензора обратной эффективной массы.
Если эффективная масса- скаляр, то ускорение будет получать электрон всегда по направлению силы: 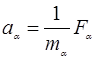
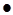 это соотношение для тензора
это соотношение для тензора 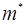 справедливо для значений массы, равной
справедливо для значений массы, равной 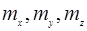
Особенности динамики электрона в кристалле связаны с одновременным действием внешней силы и кристаллического поля на электрон, обладающего волновыми свойствами.
Физический смысл понятия эффективной массы
Нарисуем графики: E( 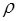 );
); 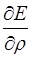 ;
; 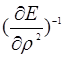
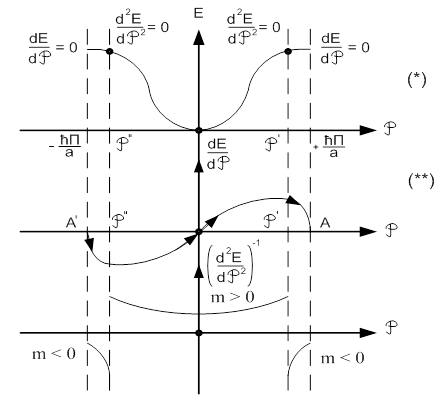
При 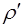 и
и 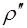 наблюдается отклонение E(
наблюдается отклонение E( 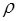 ) от квадратичной зависимости, вследствие того, что с ростом энергии увеличивается волновой вектор электрона, длина электрона
) от квадратичной зависимости, вследствие того, что с ростом энергии увеличивается волновой вектор электрона, длина электрона 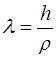
(*) уменьшается и становится сравнимой с межплоскостным расстоянием, что приводит к Брэгговскому отражению электронных волн от атомных плоскостей – с ростом  возрастает доля отраженной волны, а затем торможение при
возрастает доля отраженной волны, а затем торможение при 
(**) скорость v:
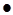 в пределах от
в пределах от 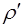 до
до 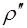 электрон движется как свободный.
электрон движется как свободный.
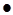 при
при 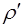 - скорость достигает максимального значения, а затем в следствии торможения решеткой, падает до нуля.
- скорость достигает максимального значения, а затем в следствии торможения решеткой, падает до нуля.
Этому соответствует смена знака 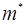 с плюса на минус.
с плюса на минус.
Затем электрон отражается от точки 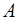 к точки
к точки  и снова движется в прежнем направлении, т.е. электрон совершает периодические движения во внешнем электрическом поле.
и снова движется в прежнем направлении, т.е. электрон совершает периодические движения во внешнем электрическом поле.
Вывод: эффективная масса 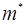 в отличие от обычной массы не постоянна, она не является мерой инерции и не связана с силами тяготения.
в отличие от обычной массы не постоянна, она не является мерой инерции и не связана с силами тяготения.
Дата добавления: 2015-08-26; просмотров: 1790;
